WHAT IS SOHCAHTOA?
Sine, cosine, and tangent are the three fundamental trigonometric functions in trigonometry. To find the value of these trigonometric functions, we simply get the ratio of the two sides of a right triangle. SOHCAHTOA is a mnemonic used to remember the formula of these three trigonometric functions easily.
The table below shows the meaning behind the mnemonic SOHCAHTOA and its corresponding formula.
| Meaning | Formula | |
| SOH | SOH means $\sin \theta$ is equal to the opposite divided by the hypotenuse. | $\sin \theta =\frac{opposite}{hypotenuse}$ or $\sin \theta =\frac{o}{h}$ |
| CAH | CAH means $\cos \theta$ is equal to the adjacent divided by the hypotenuse. | $\cos \theta=\frac{adjacent}{hypotenuse}$ or $\cos \theta=\frac{a}{h}$ |
| TOA | TOA means $\tan \theta$ is equal to the opposite divided by the adjacent. | $\tan \theta =\frac{opposite}{adjacent}$ or $\tan \theta =\frac{o}{a}$ |
There are other ways to remember the three fundamental trigonometric functions aside from the mnemonic SOHCAHTOA. The list below shows some of the other mnemonics one can use to familiarize yourselves with trigonometric functions.
| Mnemonics for Sine, Cosine, and Tangent |
| Some Of Her Children Are Having Trouble Over Algebra |
| She Offered Her Cat A Heaping Teaspoon Of Acid |
| Saddle Our Horses, Canter Away Happily, To Other Adventures. |
| School! Oh, How Can Anyone Have Trouble Over Academics? |
| Some Old Horse Caught Another Horse Taking Oats Away. |
| Two Old Angels Skipped Over Heaven Carrying Ancient Harps |
| The Ordinary Army Simple Officers Have Curly Auburn Hair |
WHEN ARE THE PARTS OF A RIGHT TRIANGLE?
SOHCAHTOA can help us determine unknown measure angles and unknown lengths of the sides of the right triangle. To effectively use the concept of SOHCAHTOA, one must know the parts of a right triangle. The figure below shows a right triangle and its parts.
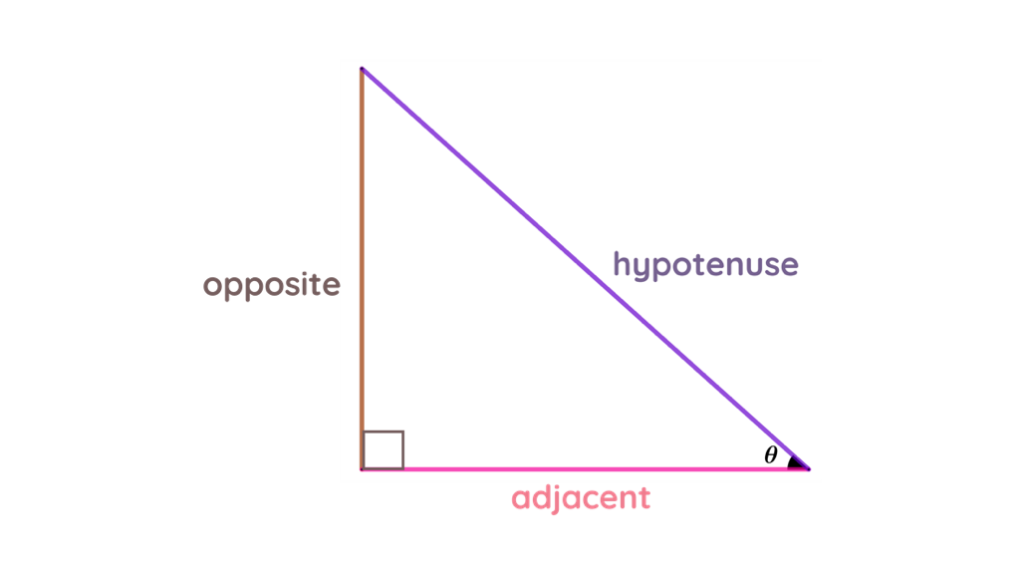
The hypotenuse is the longest side of a right triangle. It is the side opposite to the right angle.
The opposite side is the side opposite to the given angle.
The adjacent side is the non-hypotenuse side that is next to the given angle.
Always remember that the adjacent side is always next to the given angle.
Say, for example, we have ∆ABC as shown in the figure below:

The given angle is ∠B. Hence,
$\bar{AB}$ is the hypotenuse;
$\bar{BC}$ is the adjacent side; and
$\bar{AC}$ is the opposite side.
Identifying the parts of a right triangle is one of the essential concepts in using SOHCAHTOA.
EXAMPLE
Identify the sides of a right triangle given the figure below.
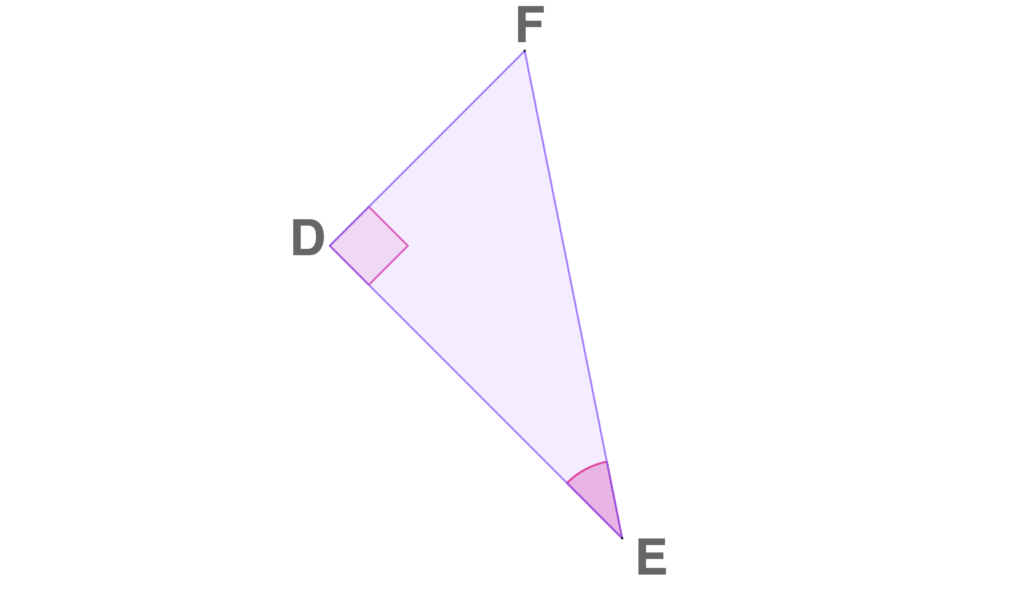
SOLUTION
Given that the right angle is ∠D, we can easily say that $\bar{FE}$ is the hypotenuse of ΔDEF. Since the given acute angle is represented by ∠E, it follows that $\bar{DF}$ is the opposite side of ∠E and $\bar{DE}$ is the adjacent side of ∠E
WHEN TO USE SOHCAHTOA?
Before using the formula of SOHCAHTOA, make sure that the given triangle is a right triangle. Moreover, when given a right triangle, it is only possible to use SOHCAHTOA if they met the following conditions:
- two sides of a right triangle are given; or
- one side of a right triangle and one acute angle is given.
Let us look at the different examples of the right triangles below.

HOW TO USE SOHCAHTOA?
SOHCAHTOA is used to find the unknown measures of a right triangle, whether there is a missing angle or missing length of a right triangle.
SOLVING UNKNOWN ANGLES
To solve unknown angles of a right triangle, make sure that lengths of the two sides of the right triangle are given. Then, one can already proceed to follow the steps below:
- Identify the hypotenuse, the adjacent side, and the opposite side.
- Use the appropriate formula given by the SOHCAHTOA.
- Solve for the unknown angle by using a scientific calculator. (Note: To solve for the unknown angle in your calculator, use the inverse trigonometric ratios that looks like either one of these: $\sin ^{-1}$, $\cos ^{-1}$ and $\tan ^{-1}$).
- Do not forget to round off to two decimal places.
EXAMPLE #1
What is the measure of ∠C?
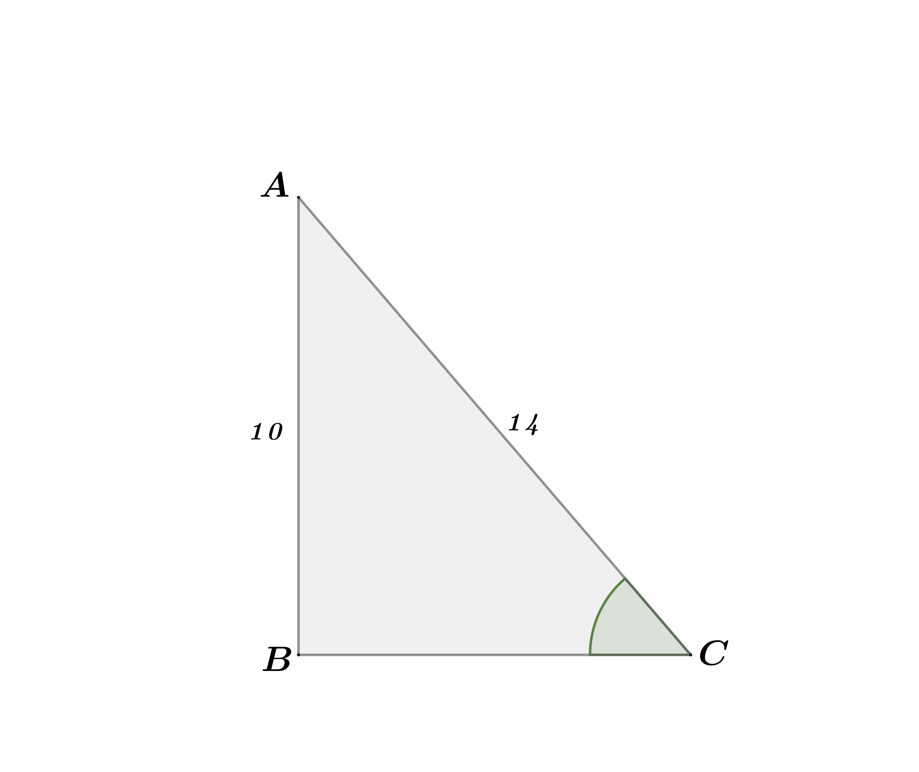
SOLUTION
Step 1: Since∠C is the unknown angle, we will base the adjacent and opposite side from ∠C. Thus, the adjacent side of ∠C is $\bar{BC}$, the opposite side is $\bar{BA}$, and the hypotenuse is $\bar{AC}$.
Step 2: As shown in the figure, $\bar{BA}=10$ and $\bar{AC}=14$. Hence, we have an opposite side and a hypotenuse to input in the formula.
Step 3: Using SOH in SOHCAHTOA will result to:
$\sin \theta =\frac{o}{h}$
$\sin \theta =\frac{10}{14}$
$\theta =\sin ^{-1}(\frac{10}{14})$
$\theta =45.58$
Therefore, the measure of $∠C$ is 45.58.
EXAMPLE #2
What is the measure of $∠L$?
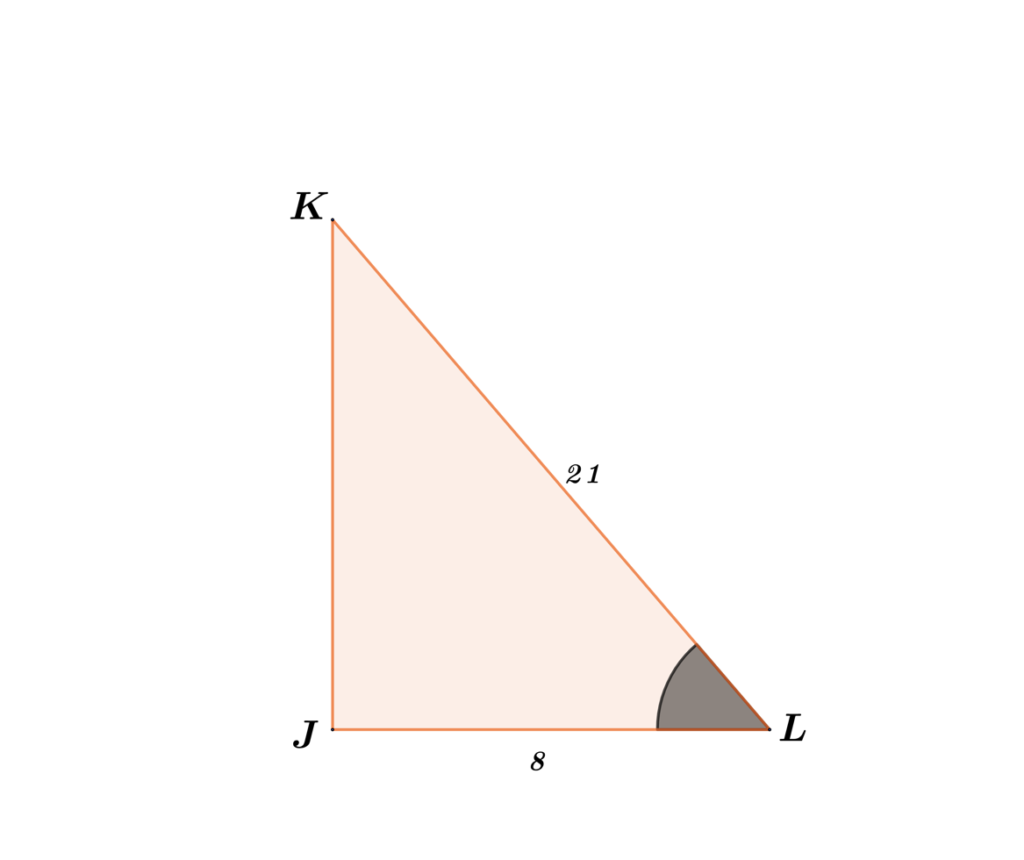
SOLUTION
Step 1: Since $∠L$ is the unknown angle, we will base the adjacent and opposite side from $∠L$. Hence, the adjacent side of $∠L$ is $\bar{JL}$, the opposite side is $\bar{JK}$, and the hypotenuse is $\bar{KL}$.
Step 2: In the figure, $\bar{JL}=8$ and $\bar{KL}=21$. Thus, we have a known value for the adjacent side and hypotenuse.
Step 3: Use the CAH in SOHCAHTOA.
$cos \theta=\frac{a}{h}$
$cos \theta=\frac{8}{21}$
$\theta=cos^{-1}(\frac{8}{21})$
$\theta=67.61$
Therefore, ∠L = 67.61.
EXAMPLE #3
Find the measure of $∠U$.
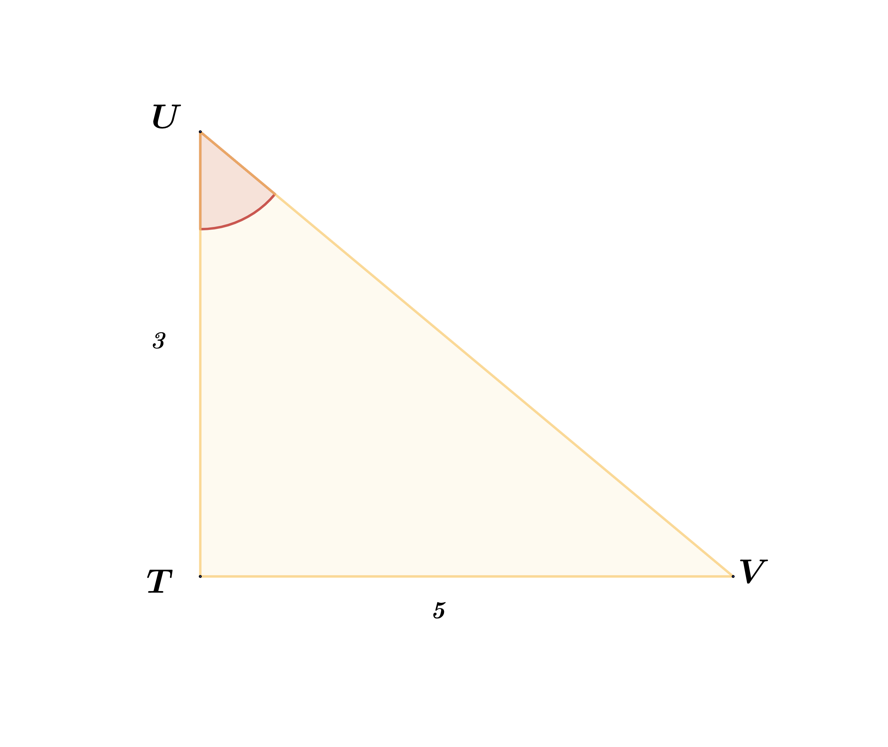
SOLUTION
Step 1: Since ∠U is the unknown angle, we will base the opposite and adjacent side from ∠U. Thus, the adjacent side is $\bar{UT}$, the opposite side is $\bar{TV}$, and the hypotenuse is $\bar{UV}$.
Step 2: In ∆TUV, the measures for $\bar{UT}$ and $\bar{TV}$ is already given wherein $\bar{UT}=3$ and $\bar{TV}=5$.
Step 3: Since we have the given value for the adjacent and opposite side of ∆TUV, use TOA in SOHCAHTOA which means:
$\tan \theta =\frac{o}{a}$
$\tan \theta =\frac{5}{3}$
$\theta =\tan^{-1}(\frac{5}{3})$
$\theta =59.04$
Therefore, the measure of ∠U is 59.04.
SOLVING UNKNOWN MEASURES OF SIDE
To solve an unknown measure of the side of a right triangle, check if the measure of another side of the right triangle and one acute angle is given. Then, derive different formulae from SOHCAHTOA to find the value of the missing side.
The table below shows the different formulae derived from SOHCAHTOA.
| Missing Opposite Side | Missing Adjacent Side | Missing Hypotenuse | |
| SOH | $o=(\sin \theta)(h)$ | – | $h=\frac{o}{\sin \theta}$ |
| CAH | $a=(\cos \theta)(h)$ | $h=\frac{o}{\cos \theta}$ | |
| TOA | $o=(\tan \theta)(a)$ | $a=\frac{o}{\tan \theta}$ |
To find unknown measure of the side of a right triangle,
- Identify the part of the triangle in reference to the given angle.
- Use the appropriate formula derived from the SOHCAHTOA.
- Solve for the unknown angle by using a scientific calculator.
- Do not forget to round off to two decimal places.
EXAMPLE #1
Determine the measure of $\bar{EN}$.
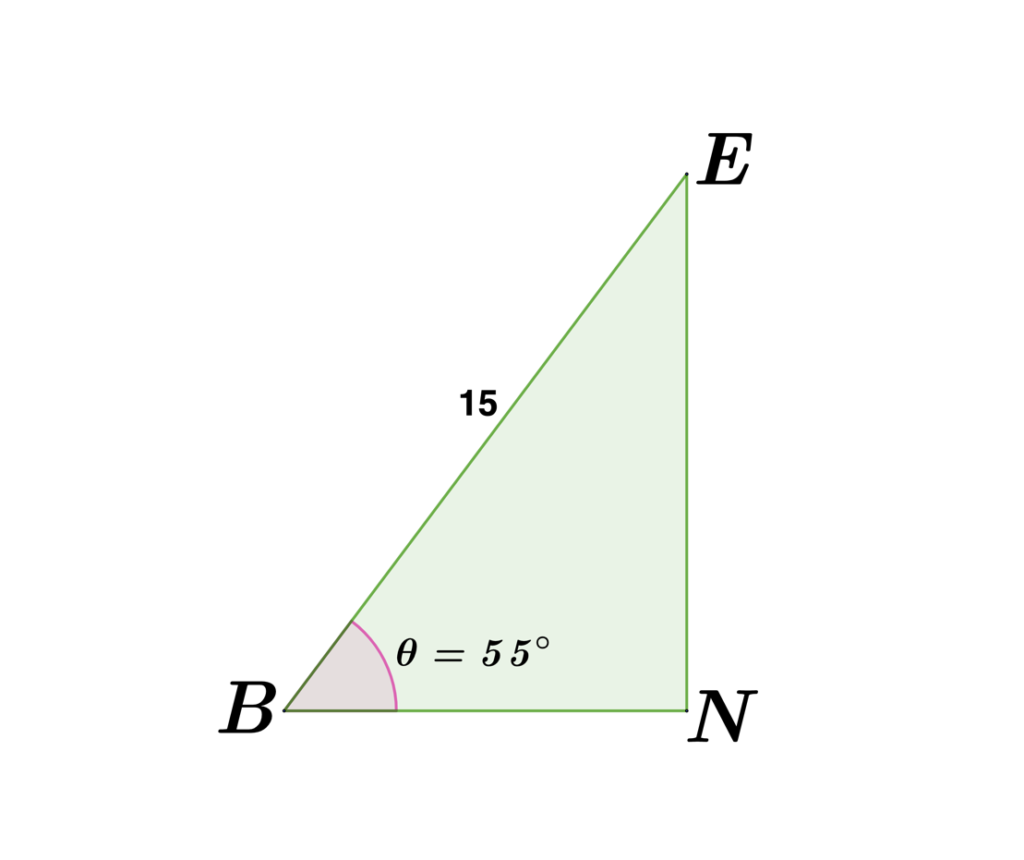
SOLUTION
Step 1: Use ∠B as the reference angle to determine the adjacent and opposite side. Thus, $\bar{BN}$ is the adjacent side of ∠B, $\bar{EN}$ is the opposite side of ∠B, and $\bar{BE}$ is the hypotenuse.
Step 2: Given $\bar{EB}=15$ and ∠B=55°, use the derived formula for the missing opposite side. Thus,
$o=(\sin\theta)(h)$
$o=\sin(55^{\circ })(15)$
$o=12.29$
Therefore, $\bar{EN}=12.29$
EXAMPLE #2
Solve for the length of $\bar{CT}$.
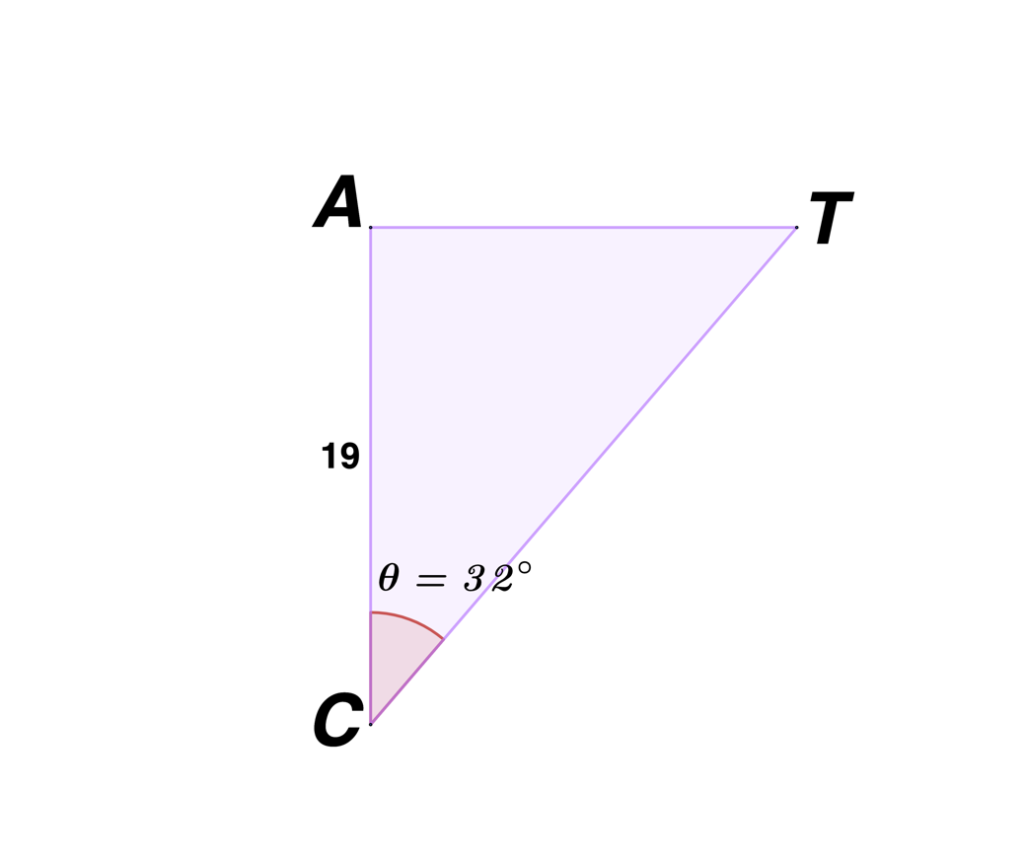
SOLUTION
Step 1: Use ∠C as the reference angle to determine the adjacent and opposite side. Hence, $\bar{CA}$ is adjacent to ∠C, $\bar{AT}$ is opposite to ∠C, and $\bar{BC}$ is the hypotenuse.
Step 2: Given $\bar{AC}$ and ∠C=32°, use the derived formula for the missing length of the hypotenuse. Thus,
$h=\frac{a}{\cos \theta}$
$h=\frac{19}{\cos(32^{\circ })}$
$h=22.04$
Therefore, the measure of $\bar{CT}$ is 22.04.
EXAMPLE #3
Find the unknown measure of the sides and angles of ∆DOR.
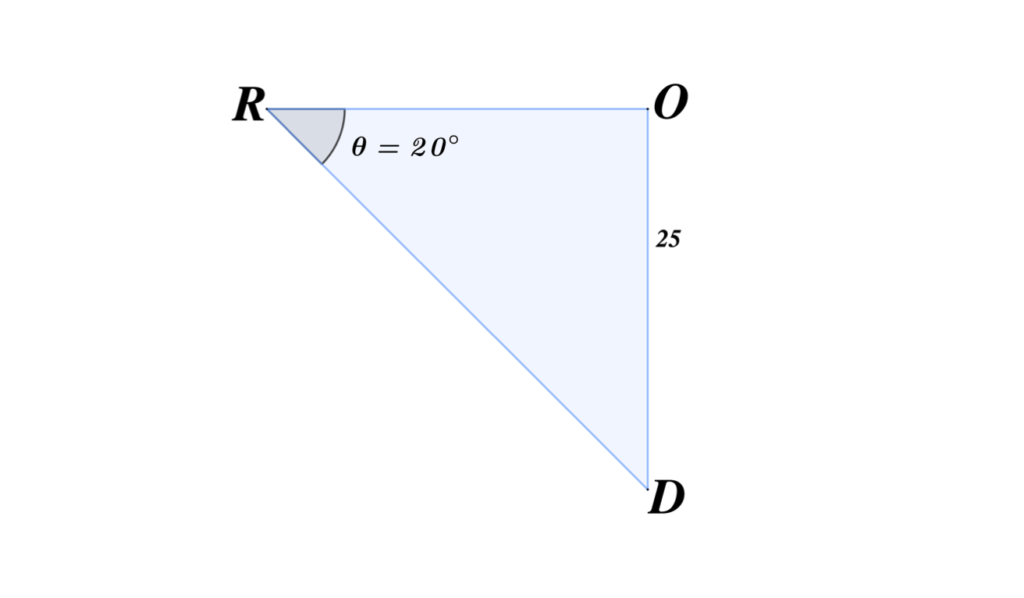
SOLUTION
Step 1: Use ∠R to determine the adjacent and opposite side. Hence, $\bar{RO}$ is the adjacent of ∠R, $\bar{OD}$ is the opposite side of ∠R, and $\bar{RD}$ is the hypotenuse of ∆DOR.
Step 2: As shown in the figure, the given values are ∠R=20° and $\bar{OD}$ which is the opposite side of ∠R. By SOHCAHTOA, we will use the derived formula of TOA to solve the length of $\bar{RO}$. Thus,
$a=\frac{o}{\tan \theta}$
$a=\frac{25}{\tan (20^{\circ })}$
$a=68.69$
Step 3: Use the Pythagorean theorem to find the measure of the hypotenuse $\bar{RD}$. Thus,
$\bar{RD}=\sqrt{(\bar{RO})^{2}+(\bar{OD})^{2}}$
$\bar{RD}=\sqrt{(68.69)^{2}+(25)^{2}}$
$\bar{RD}=\sqrt{4718.32+625}$
$\bar{RD}=\sqrt{5343.32}$
$\bar{RD}=73.10$
Step 4: Find the measure of angles ∠O and ∠D. Given the ∆DOR, we can already note that ∠O is a right angle. Hence, ∠O=90°. To find ∠D, use the triangle angle sum theorem, which states that the sum of the three interior angles of a triangle is always equal to 180°. Thus,
∠D+∠O+∠R=180°
∠D+90°+20°=180°
∠D+110°=180°
∠D=180°-110°
∠D=70°
Therefore, the measures of the unknown sides and angles are $\bar{RO}=68.69$, $\bar{RD}=73.10$, $∠O=90°$, and $∠D=70°$.
SOLVING WORD PROBLEMS WITH SOHCAHTOA
When it comes to solving word problems, there is no exact step-by-step rule that one needs to follow, as every problem has its own approach to come up with the answer. However, here are some of the strategies that may help you solve word problems involving trigonometric functions:
- Read and carefully analyze the problem. Make sure that you understand the whole idea or concept of the problem.
- Jot down all the information given. In this way, you can quickly pinpoint the unknown.
- If possible, sketch the situation as this will also help you fully understand the situation or problem.
- Do not round off decimal numbers in the middle of your solution, as this can sometimes make a huge difference with the final answer.
EXAMPLE #1
Gwyneth is planning to build a mainsail for her small boat. The sketch for her mainsail is shown in the figure below. What will be the dimension of her mainsail?

SOLUTION
Step 1: Label the points of a triangle formed in the figure by assigning random letters. Thus,

Labeling makes it easier to determine the missing parts of the triangle and the process that should be done to it.
Step 2: From the triangle made in Step 1, we can now name the parts of the right triangle where ∠T=45° is the reference angle. Thus, $\bar{TA}$ is the side adjacent to ∠T, $\bar{AS}$ is side opposite ∠T, and $\bar{TS}$ is the hypotenuse.
Step 3: From the given information, the first side that we can solve is the hypotenuse. Hence, we will use the derived form of hypotenuse given the adjacent side and ∠T. Therefore,
$h=\frac{a}{\cos \theta}$
$h=\frac{8}{\cos(45^{\circ })}$
$h=8\sqrt{2}$
Step 4: Since we are asked to find the dimensions of the mainsail, find $\bar{AS}$ in terms of the Pythagorean theorem. Thus,
$\bar{AS}=\sqrt{(8\sqrt{2})^{2}-(8)^{2}}$
$\bar{AS}=\sqrt{128-64}$
$\bar{AS}=\sqrt{64}$
$\bar{AS}=8$
Note that in step 3, we did not use the value of $8\sqrt{2}=11.31$ as using 11.31 in Step 4 will significantly affect the measure of $\bar{AS}$.
Therefore, the dimensions of the mainsail Gwyneth wants to create is 8 ft x 8 ft x 11.31 ft.
EXAMPLE #2
A mathematically inclined cat sits on top of a branch that is 10 ft tall. The cat’s ball is 15 ft away from the base of the branch he was sitting. What is the angle between the cat’s point of view from his ball? How about the distance of the cat from the ball?
SOLUTION
Step 1: Illustrate the situation to understand the problem.

Step 2: Say, the angle from the cat’s point of view is denoted by ∠C. Hence, we can note that the adjacent side measures 10 ft. and the opposite side measures 15 ft. in reference to ∠C.
Step 3: Use the formula of TOA.
$\tan \theta =\frac{o}{a}$
$\tan \theta =\frac{15}{10}$
$\theta =\tan ^{-1}(\frac{15}{10})$
$\theta =56.31^{\circ}$
Step 4: To find the distance of the cat from his ball, use Pythagorean theorem. Since the value of the adjacent and opposite is already given, simply substitute it to the Pythagorean theorem formula. Thus,
$c^{2}=a^{2}+b^{2}$
$c=\sqrt{(10)^{2}+(15)^{2}}$
$c=\sqrt{100+225}$
$c=\sqrt{325}$
$c=18.03$
Therefore, the angle of the cat’s point of view to the ball is approximately $$ and the distance of the cat from the ball is approximately 18.03 ft.
Recommended Worksheets
Scalene Triangles (Summer Camp Themed) Math Worksheets
Isosceles Triangles (Holiday Cruise Ship Themed) Math Worksheets
Acute Triangles (City Themed) Math Worksheets









