Law of Sines | Proof, What Is?, History, How To Use?

What will I learn from this article?

After reading this article, you will be able to:

define the Law of Sines;
know the history of Law of Sines;
prove the Law of Sines;
determine the ambiguous case of triangle solutions; and
apply the knowledge of the Law of Sines in solving problems.

What is the Law of Sines?

The Law of Sines establishes the relationship between a non-right triangle or oblique triangle’s sides and angles. In trigonometry, the law of sines and cosines are essential rules for solving a triangle.

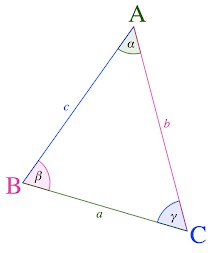
The Law of Sines states that the ratio of the length of a triangle to the sine of the opposite angle is the same for all sides and angles in a given triangle.

Mathematically, it can be defined as:

$\frac{sinsin \alpha}{a} = \frac{sinsin\beta}{b} = \frac{sinsin\gamma}{c}$

where

a, b and c are the lengths of a triangle; and
$\alpha, \beta, \gamma$ and are the opposite angles.

By taking the reciprocals, the Law of Sines can also be written as

$\frac{a}{sinsin \alpha} = \frac{b}{sinsin\beta} = \frac{c}{sinsin\gamma}$

or even a collection of three equations such as:

$\frac{a}{b} = \frac{sinsin\alpha}{sinsin\beta}; \frac{a}{c} = \frac{sinsin\alpha}{sinsin\gamma}; \frac{b}{c} = \frac{sinsin\beta}{sinsin\gamma}$

When two angles and a side are known, the law of sines can be used to compute the remaining sides of a triangle — a process known as triangulation.

To summarize, the formulae that we can use in Law of Sines are shown in the table below.

Law of Sines Formula

$\frac{sinsin \alpha}{a} = \frac{sinsin\beta}{b} = \frac{sinsin\gamma}{c}$

$\frac{a}{sinsin \alpha} = \frac{b}{sinsin\beta} = \frac{c}{sinsin\gamma}$

$\frac{a}{b} = \frac{sinsin\alpha}{sinsin\beta}; \frac{a}{c} = \frac{sinsin\alpha}{sinsin\gamma}; \frac{b}{c} = \frac{sinsin\beta}{sinsin\gamma}$

History of Law of Sines

According to Ubiratàn D’Ambrosio and Helaine Selin, the spherical law of sines was discovered in the tenth century. It has been attributed to Abu Mahmud Khojandi, Abu al-Wafa’ Buzjani, Nasir al-Din al-Tusi, and Abu Nasr Mansur, among others.

In the book of Ibn Mu ‘ādh al- Jayyānnī, The book of unknown arcs of a sphere, which was published in the 11^th century, includes the general law of sine. Nasīr al-Dīn al-Tūsī later stated the plane law of sines in the 13^th century. In his book, On the Sector Figure, he wrote the law of sines for plane and spherical triangles, provided with proofs.

According to Glen Van Brummelen, “the Law of Sines is really Regiomontanus’ foundation for his solutions of right-angled triangles in Book IV, which in turn serve as the foundation for his solutions of general triangles.” Regiomontanus was a German mathematician in the fifteenth century.

What is the proof of Law of Sines?

To prove the law of sines, consider a ∆ABC as an oblique triangle.

If ∆ABC is an acute triangle, then ∠ABC is an acute angle. In that case, draw an altitude from the vertex of C to the side of $\overline{AB}$.

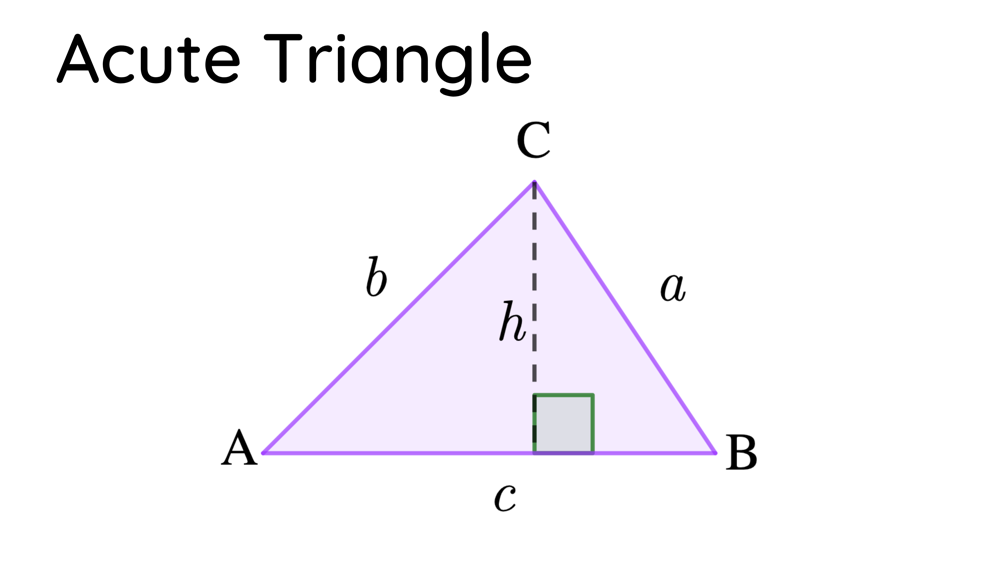
In an acute triangle, the altitude lies inside the triangle. Hence, if we denote h as the height of the altitude in ∆ABC, then using the rules of SOHCAHTOA, we will have:

sinsin A = $\frac{h}{b}$ and sinsin B = $\frac{h}{a}$

If we are to compute the value in terms of h, the equation will be:

h = bsinsin A and h = asinsin B .

Thus, we can now say that

bsinsin A = asinsin B .

Moreover, if we put a and b to the left and right side of the equation, respectively. We will come up with:

$\frac{a}{sinsin A} = \frac{b}{sinsin B}$

Following the same argument, drawing an altitude from A to BC will give us

$\frac{b}{sinsin B} = \frac{c}{sinsin C}$

Thus,

$\frac{a}{sinsin A} = \frac{b}{sinsin B} = \frac{c}{sinsin C}$

If ∆ABC is an obtuse triangle, then ∠ABC is an obtuse angle. In that case, draw an altitude from the vertex of C to the side of $\overline{AB}$.

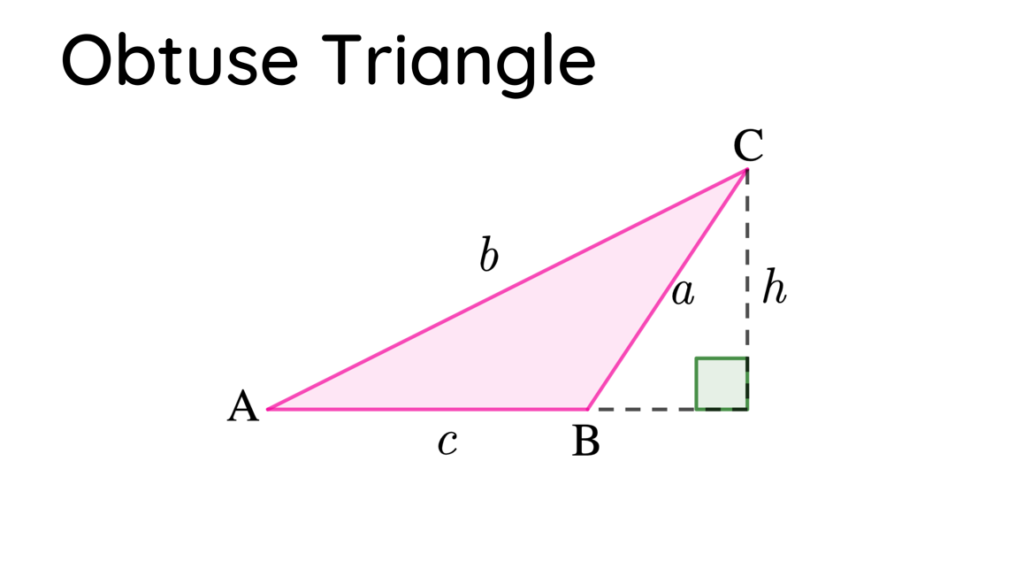
In an obtuse triangle, the altitude lies outside the triangle. Since we are going to use the exterior angle of B, then the angle is described as 180°-B.

Hence, if we denote h as the height of the altitude in ∆ABC, then using the rules of SOHCAHTOA, we will have:

sinsin A = $\frac{h}{b}$ and sinsin (180° – B) = $\frac{h}{a}$

Applying trigonometric identities, sinsin 180° – B = sinsin B . Thus, if we are to compute the value in terms of h, the equation will be:

h = b sinsin A and h = a sinsin B .

Thus, we can now say that

b sinsin A = a sinsin B .

Moreover, if we put a and b to the left and right side of the equation, respectively. We will come up with:

$\frac{a}{sinsin A} = \frac{b}{sinsin B}$

Following the same argument, drawing an altitude from A to $\overline{BC}$ will give us

$\frac{b}{sinsin B} = \frac{c}{sinsin C}$

Thus,

$\frac{a}{sinsin A} = \frac{b}{sinsin B} = \frac{c}{sinsin C}$

How to use Law of Sines?

The following are examples of solving a problem using the law of sines.

Given one side and two angles

To solve triangles by Law of Sine given one side and two angles, consider the following steps below:

Determine the angle measure of the unknown. Since there are only three interior angles in a triangle, and the sum of the angle measure of a triangle is 180°, then it will be easy to solve for the unknown.
Use the formula $\frac{a}{sinsin A} = \frac{b}{sinsin B} = \frac{c}{sinsin C}$ to solve for the unknown side measures.

Example

Solve for the unknown angle measure and side measures given b = 12, ∠A = 54°, and ∠C = 58°.

Solution

Step 1: Solve for the missing angle measure using the sum of the interior angles of a triangle. Thus,

∠B = 180° – ∠A + ∠C∠B = 180° – 54° + 58°∠B = 180° – 112°∠B = 68°

Step 2: Use the Law of Sines to determine the unknown side measures. Thus,

To find a using the side measure of b:

$\frac{a}{sinsin A} = \frac{b}{sinsin B} = \frac{a}{sinsin 54} = \frac{12}{sinsin 68}a = \frac{12sinsin 54}{sinsin 68}a$ = 10.47

To find c using the side measure of b:

$\frac{b}{sinsin B} = \frac{c}{sinsin C} = \frac{12}{sinsin 68} = \frac{c}{sinsin 58}c = \frac{12sinsin 58}{sinsin 68}c$ = 10.98

Therefore, ∠B= 68°, a = 10.47, c = 10.98.

Given two sides and an opposite angle

To solve triangles by Law of Sine given two sides and an opposite angle, consider the following steps below:

Find the other opposite angle using the Law of Sines.
Determine for the possible solutions of triangle if it is possible to be an acute or obtuse triangle.
Determine the remaining unknown angle by subtracting the two known angles from 180°.
Use law of sines to find the unknown sides of the triangle.

Example #1

Determine the unknown angle measure and side measures given a = 25, c = 40, and ∠C = 120°.

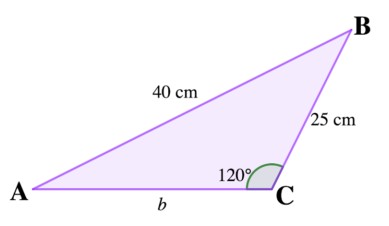
Solution

Step 1: Find the angle A in terms of angle C and side c. Thus, by Law of Sine

$\frac{a}{sinsin A} = \frac{c}{sinsin C} \frac{25}{sinsin A} = \frac{40}{sinsin 120}sinsin A (40) = sinsin 120 (25) sinsin A = \frac{120}{40}sinsin A$ = 5316

Step 2: Use the sin -1 in your calculator to determine the angle measure of A.

∠A = sinsin $^{-1}\left ( \frac{5\sqrt{3}}{16} \right )$∠A = 32.77°

Step 3: Determine for the possible solutions of triangle if it is possible to be an acute or obtuse triangle. Recall that sin 180° – θ =sin . Then, we can follow the same for ∠A. Thus,

sin 180° – 32.77° = sin 147.23°

However, given the measure of angles and the illustration of triangle, we cannot have two obtuse angle in a triangle. Thus, the only valid angle measure for A is 32.77°

Step 4: Determine ∠B. Thus, by subtracting the sum of the two known angles from 180°,

∠B = 180° – ∠A + ∠C∠B = 180° – 32.77° + 120°∠B = 180° – 152.77°∠B = 27.23°Step 5:

Solve for the measure of b using the law of sine.

$\frac{b}{sinsin B} = \frac{c}{sinsin C} \frac{b}{sinsin 27.23} = \frac{40}{sinsin 120}b = \frac{40sinsin 27.23}{sinsin 120}b$ = 21. 13

Therefore, the measure of the unknown angles and sides are ∠A = 32.77° ,
∠B = 27.23° and b = 21.13 cm.

Example #2

What is the measure of the unknown angles and side if ∠A = 35°, a = 15, and b = 9?

Solution

Step 1: Find the angle measure of B in terms of ∠A and a. Thus,

$\frac{b}{sinsin B} = \frac{a}{sinsin A} \frac{9}{sinsin B} = \frac{15}{sinsin 35}sinsin B(15) = sinsin35 (9) sinsin B = \frac{35}{15}sinsin B$ = 0.34

Step 2: Use the sin -1 in your calculator to determine the angle measure of B.

∠B = sinsin^-1 (0.34}∠B = 19.89°

Step 3: Determine for the possible solutions of triangle if there is a possibility of it being an acute or an obtuse triangle. Recall that sin 180° – θ=sin . Then, we can follow the same for ∠B. Thus,

sinsin (180° – 19.89°) = sinsin 160.11°

However, if we look back at the value of ∠A = 35°, it is impossible for ∠B to be of measure 160.11° since the sum of the interior angles of a triangle is only 180°. Thus, we will only proceed with the acute angle measure of B which is

∠B = 19.89°.

Step 4: Determine ∠C. Thus, by subtracting the sum of the two known angles from 180°,

∠C = 180° – (∠A + ∠B)∠C = 180° – (35° + 19.89°)∠C = 180° – (54.89°)∠C = 125.11°

Step 5: Solve for the measure of c using the law of sine.

$\frac{a}{sinsin A} = \frac{c}{sinsin C} \frac{15}{sinsin 35} = \frac{c}{sin 125.11}c = \frac{40sin 35}{sinsin 125.11}$c = 28.05

Therefore, the measure of the unknown angles and sides are ∠B=19.89° ,
∠C = 125.11° and c = 21.05.

Example #3

Solve for triangle ∆ABC given a = 18, ∠A=25°, and b = 30.

Solution

Step 1: Find the angle measure of B in terms of ∠A and a. Thus,

$\frac{b}{sinsin B} = \frac{a}{sinsin A} \frac{30}{sinsin B} = \frac{18}{sinsin 25}sinsin B (18) = sinsin 25 (30) sinsin B = \frac{25}{18}sinsin B$ = 0.70

Step 2: Use the sinsin^-1 in your calculator to determine the angle measure of B.

∠B = sinsin^-1 (0.70)∠B = 44.23°

Step 3: Determine the possible solutions of triangle if there is a possibility of it being an acute or an obtuse triangle. Recall that sin 180° – θ = sin . Then, we can follow the same for ∠B. Thus,

sinsin (180° – 44.23°) = sinsin 135.77°

Step 4: Since we have two possible values for ∠B, then it means the triangle can be an acute or an obtuse triangle. Thus, we will find the other angles for each case.

If ∆ABC is an acute triangle, then ∠B = 44.23°. Determine ∠C. Thus, by subtracting the sum of the two known angles from 180°,

∠C = 180° – (∠A + ∠B)∠C = 180° – (25° + 44.23°)∠C = 180° – (69.23°)∠C = 110.77°

If ∆ABC is an obtuse triangle, then ∠B = 135.77°. Determine ∠C. Thus, by subtracting the sum of the two known angles from 180°,

∠C = 180° – (∠A + ∠B)∠C = 180° – (25° + 135.77°)∠C = 180° – (160.77°)∠C = 19.23°

Step 5: Solve for the measure of c using the law of sine in terms of a and ∠A.

If ∆ABC is an acute triangle, then ∠C = 110.77°.

$\frac{a}{sinsin A} = \frac{c}{sinsin C} \frac{18}{sinsin 25} = \frac{c}{sinsin110.77}c = \frac{18sinsin110.77}{sinsin 25}c$ = 39.82

If ∆ABC is an obtuse triangle, then ∠C = 19.23°.

$\frac{a}{sinsin A} = \frac{c}{sinsin C} \frac{18}{sinsin 25} = \frac{c}{sinsin 19.23}c = \frac{18sinsin 19.23}{sinsin 25}c$ = 14.03

Therefore,

If ∆ABC is an acute triangle, then the measure of the unknown angles and side are ∠B = 44.23°, ∠C = 110.77° and c = 39.82; and
If ∆ABC is an obtuse triangle, then the measure of the unknown angles and side are ∠B = 135.77°, ∠C = 19.23°and c = 14.03.

Example #4

What are the unknown angles and side of ∆ABC is a = 6, b = 13, and ∠A = 35°?

Solution

Step 1: Find the angle measure of B in terms of ∠A and a. Thus,

$\frac{b}{sinsin B} = \frac{a}{sinsin A} \frac{13}{sinsin B} = \frac{6}{sinsin 35}sinsin B (6) = sinsin 35 (13) sinsin B = \frac{35}{6}sinsin B$ = 1.24

However, it is impossible for |sin B | ≤ 1 for any angle B.

Therefore, there is no solution.

What is the ambiguous case for triangle solutions?

When the law of sines is used to determine the side of a triangle, an ambiguous case occurs when two distinct triangles can be constructed using the data provided (i.e., there are two different possible solutions to the triangle).

In an ambiguous case, if two sides and the opposite angle of a triangle are known, there are three possibilities:

The triangle does not exist;
There are two distinct triangles; and
There is exactly one triangle.

For a general triangle to be ambiguous, the following conditions must be met:

The given information about the triangle is the angle and sides a and c;
The angle is acute;
The side measure of a is shorter than the side c; and
The side measure of a is longer than the altitude h from angle , where

h =csinsin$\alpha$ .

If all of the conditions hold true, then each of the angles and β’ produces a valid triangle, which implies that both of the following conditions hold true.

Assume that we know the sides a and b and the angle A of a triangle ∆ABC. Draw the angle ∠A and the side b, and imagine that the side a is attached at the vertex at C, as shown in the figures below.

If ∠A is acute, then the altitude from C to $\overline{AB}$ has a height of h=b sinsin A .
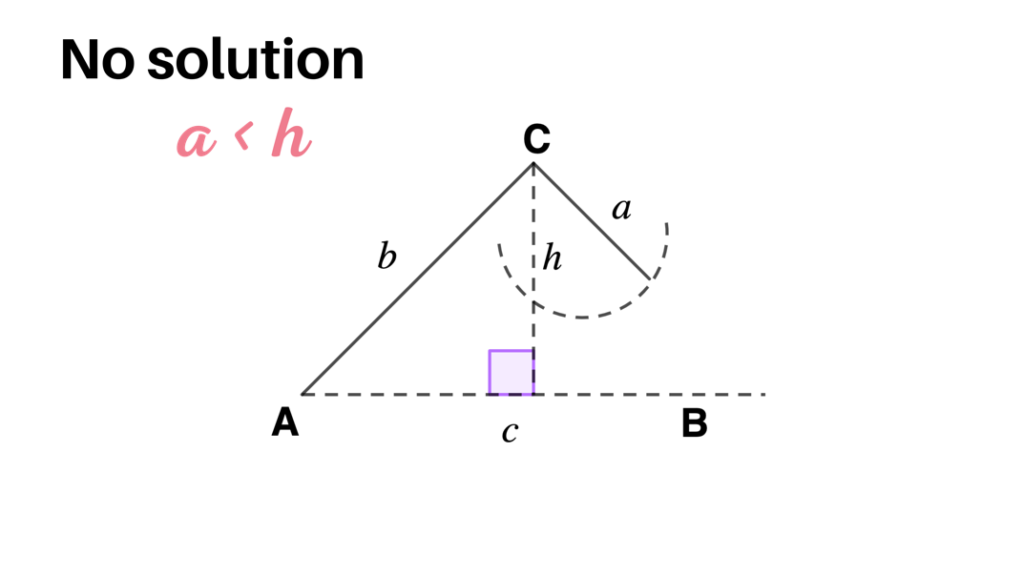
If a < h, then there is no solution.

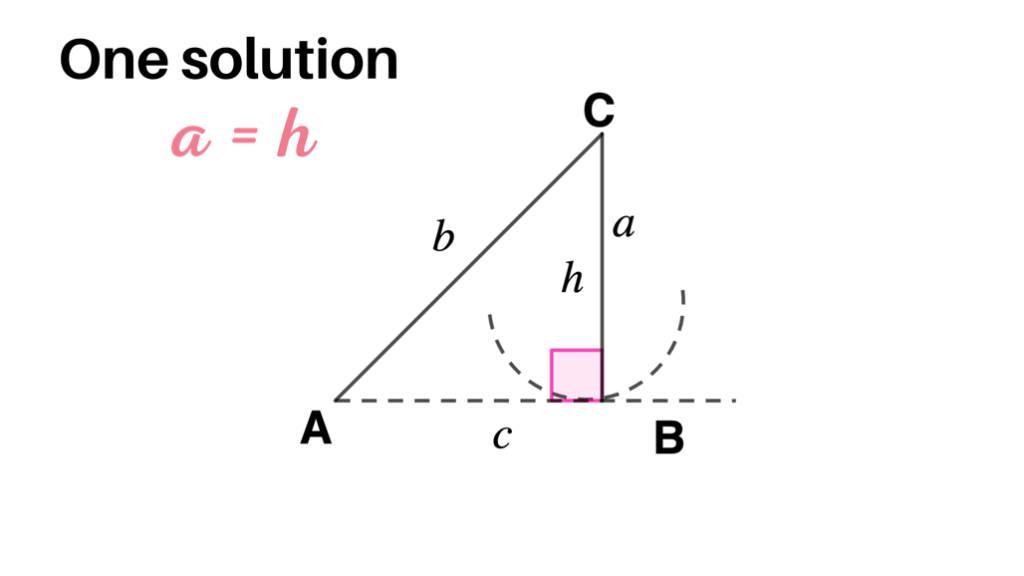
If a = h, then there is one exact solution that is a right triangle.

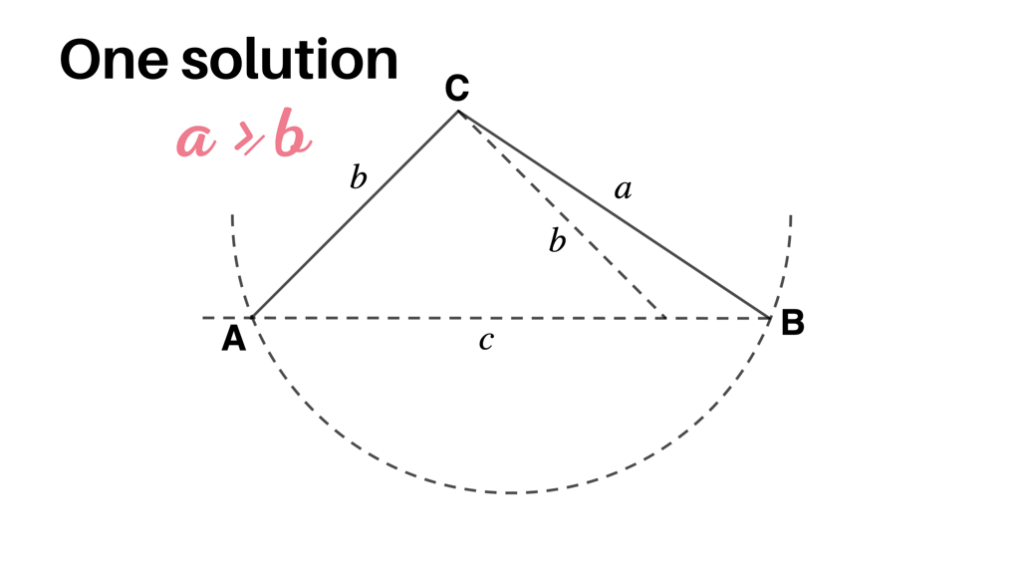
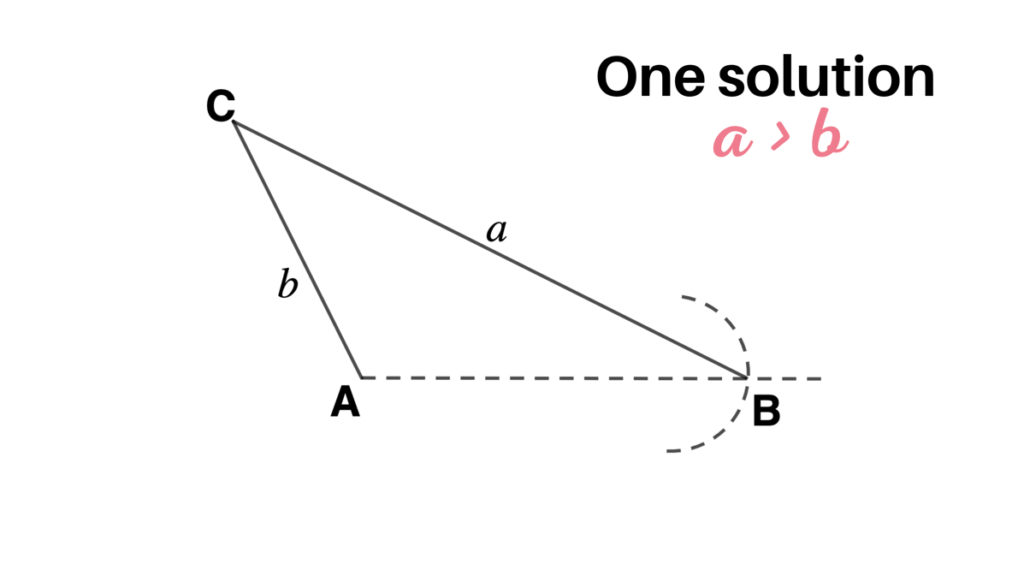
If a≥b, then there is only one solution, even though it appears that it might have two solutions since the dashed arc intersects the horizontal line at two points. However, the point of intersection to the left of A, as shown in the figure, cannot be used to determine B since it will make A an obtuse angle, and we already assumed that A was acute.

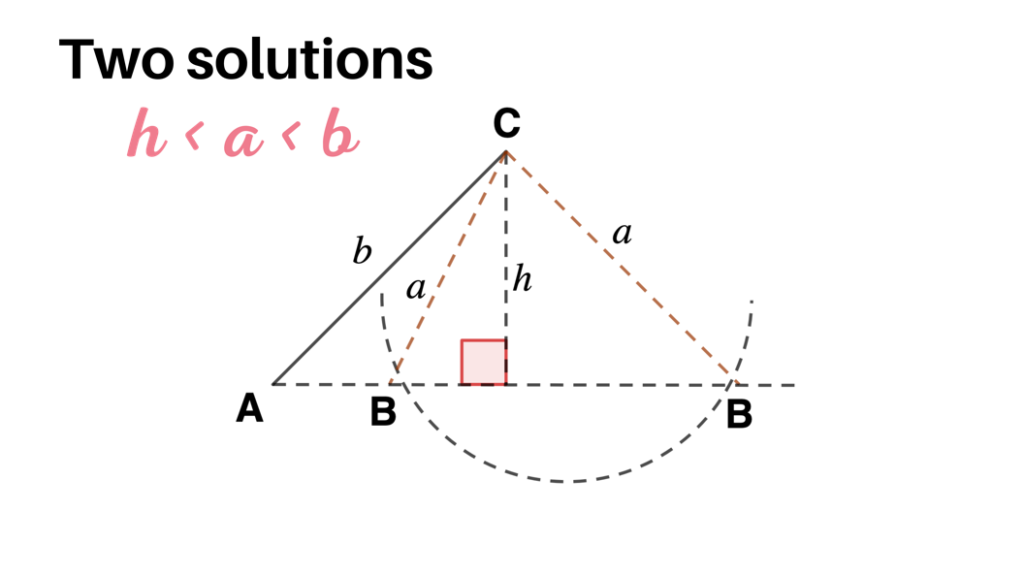
If h < a < b, then there are two solutions.

If ∠A is not acute (right or obtuse triangle)
- If a ≤b, then there is no solution.

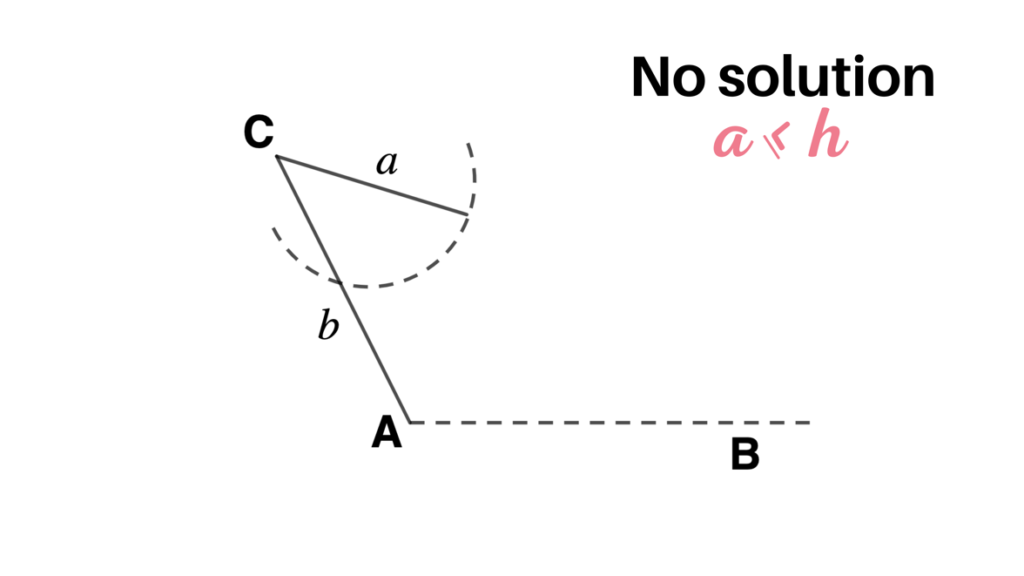
If a > b, then there is exactly one solution.

The table below summarizes the ambiguous case of solving ∆ABC by the law of sines.

	No Solution	One Solution	Two Solutions
0°<A<90°	a < bsin A	a = bsin A a ≥b	bsin A < a <b
90°<A<180°	a ≤b	a > b

What is the importance of the Law of Sine?

Generally, the law of sines is used to determine an unknown angle or side of a triangle. This law can be applied if certain combinations of triangle measurements are given.

ASA Criteria: Given two angles and a known side, identify the unknown side.
AAS Criteria: Given two angles and a side that is not included, determine the unknown side.

These two criteria will result in a unique solution, as the AAS and ASA methods are used to establish triangle congruence.

Moreover, the law of sines is not only used to solve triangles in mathematics, but it can also be helpful in our real-life such as:

determining the angle of tilt in engineering;
determining the distance measure of planets or stars in astronomy; and
determining the measurement of navigation.

Recommended Worksheets

Area of Triangles (Ice cream Themed) Worksheets
Angles (Architecture Themed) Worksheets
Acute Triangles (City Themed) Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!