Introduction
We frequently come into situations in our daily lives when the change in values of one quantity is affected by the change in values of another quantity. Two quantities can be related through proportionality. A change in one quantity’s proportion could sometimes result in a change in the proportion of another. Let us say, for instance, that if we drive faster, it takes less time to travel a certain distance. This scenario shows inverse proportionality between two quantities.
The definition of inverse proportion, how it differs from direct proportion, real-life applications, and various examples of inverse proportion will all be covered in this article.
What is Inverse Proportion?
Definition
Inverse proportion refers to the relationship between two quantities if an increase in one causes a decrease in the other and a decrease in one causes an increase in the other. In other terms, two quantities are said to be in inverse proportion if their product is equal to a constant value regardless of changes in their values.
They are said to be in inverse proportion when one quantity increases while the other decreases and vice versa. Let’s examine the table below to provide an example of inverse proportion.
| a | b |
| 2 | 32 |
| 4 | 16 |
| 8 | 8 |
| 16 | 4 |
| 32 | 2 |
| 64 | 1 |
Let us find out how the numbers show an inverse proportion by getting the product of each row. The table third column, ab, shows that the product of a and b are the same.
| a | b | a x b |
| 2 | 32 | 2×32=64 |
| 4 | 16 | 4×16=64 |
| 8 | 8 | 8×8=64 |
| 16 | 4 | 16×4=64 |
| 32 | 2 | 32×2=64 |
| 64 | 1 | 64×1=64 |
We can say that the numbers in columns a and b as “ a is inversely proportional to b” or may be represented as a∝b. Let us use the equation below to calculate the other values.
a=$\frac{64}{b}$
When b=32, a=$\frac{64}{32}$=2.
When b=16, a=$\frac{64}{16}$=4.
When b=8, a=$\frac{64}{32}$=8.
When b=4, a=$\frac{64}{4}$=16.
When b=2, a=$\frac{64}{2}$=32.
When b=1, a=$\frac{64}{1}$=64.
Formula: Inverse Proportion
The inverse proportion formula can determine a relationship between two inversely proportional quantities. Assume that x decreases when y increases and vice versa for the two values, x and y.
As an illustration, consider the relationship between speed and time. With increasing speed, it takes less time for us to cover a certain distance.
Time travel decreases as speed increases.
Time travel increases as speed decreases.
The relationship between speed and time, denoted as y and x, can be expressed mathematically as the inverse proportion formula.
Written as follows is the inverse proportional formula:
y=$\frac{k}{x}$
Take note of the following:
k is the constant of proportionality
As x decreases, y increases.
As x increases, y decreases.
The formulas below also show inverse proportionality.
y∝$\frac{1}{x}$; y=k⋅$\frac{1}{x}$; y=k ($\frac{1}{x}$)
The proportional relationship between two quantities is indicated here by the symbol .
Real World Examples of Inverse Proportion
Among the many inverse proportions scenarios are the following examples:
( 1 ) A moving object’s speed, such as a moving train, car, or ship, inversely varies with the time necessary to travel a specific distance. Less time is needed to complete a distance as speed increases.
As speed increases, time travel decreases.
As speed decreases, time travel increases.
( 2 )The number of people or workers present at work is inversely proportional to the amount of time it takes for a given number of people or workers to perform a task. This implies that the length of time it takes to complete the work increases with the number of workers and vice versa.
As the number of people or workers increases, the time it takes to finish a task decreases.
As the number of people or workers decreases, the time it takes to finish a task increases.
( 3 ) The distance between you and an ambulance as it is approaching impacts how loud its siren will be. As the ambulance approaches you, the siren becomes louder, and as it moves away, it gets quieter. The siren gets louder and quieter depending on how far away you are from the ambulance. The louder the siren, the closer you are.
As the distance between you and an ambulance increases, the sound of the siren decreases.
As the distance between you and an ambulance decreases, the sound of the siren increases.
( 4 ) The brightness of a streetlight has an inverse relationship with the distance between you and it. This indicates that the streetlight’s brightness decreases as you get farther away. The streetlight will typically be brighter if you are 50 meters from it than if you are 200 meters away.
As the distance between you and the streetlight increases, its brightness decreases.
As the distance between you and the streetlight decreases, its brightness increases.
( 5 ) The number of goods you can buy is inversely related to the price of each item. Suppose you were to consider your spending limit when purchasing some apples from the market. If the price of each apple is \$0.50 instead of \$0.75, you can buy more apples.
( 6 ) A device’s battery life is inversely proportional to the amount of time it is utilized. Consider charging a device, let us say for example a laptop, to 95% before using it. Let us suppose that after an hour of use, the battery lowers to 85%, after two hours, it reduces to 77%. A considerable and proportional decline in the battery percentage may be immediately detected with an increase in the amount of time that the device is being utilized.
Aside from the listed above, there are more examples of scenarios that involve inverse proportion. Remember that when two things are said to be in inverse proportion, a change in one quantity corresponds to a corresponding decrease or increase in the other. If we know essential information pertaining to the problem statement, the concept of inverse proportion makes it easy for us to calculate the amount or value of a missing entity.
Direct vs Inverse Proportion
Direct proportion and inverse proportion are the two main types of proportionality. To illustrate how the amounts and quantities relate to one another, a direct and inverse proportion is used. The symbol is used to denote proportionality. Let us say, for example, the variable x and y; if y is proportional to x, then it is represented as y∝x. If we have y is inversely proportional to x, then it is represented as y∝$\frac{1}{x}$. Now in both instances, the value of “y” changes in relation to “x,” or the value of “x” changes in relation to “y”. A proportionality constant is equivalent to the change in both values.
Direct Proportion
When y∝x, two variables x and y are said to be in direct proportion. This suggests that, for a constant k, y = kx. The ratio of two variables in a direct variation relationship is equal for all values.
Inverse Proportion
When y∝1/x, two variables, x and y, are said to be in inverse proportion. This means that, for a constant k, y = k/x. The product of two variables in an inverse proportion relationship is equal for all values.
To visualize the difference between direct and inverse proportion, look at the illustration below.
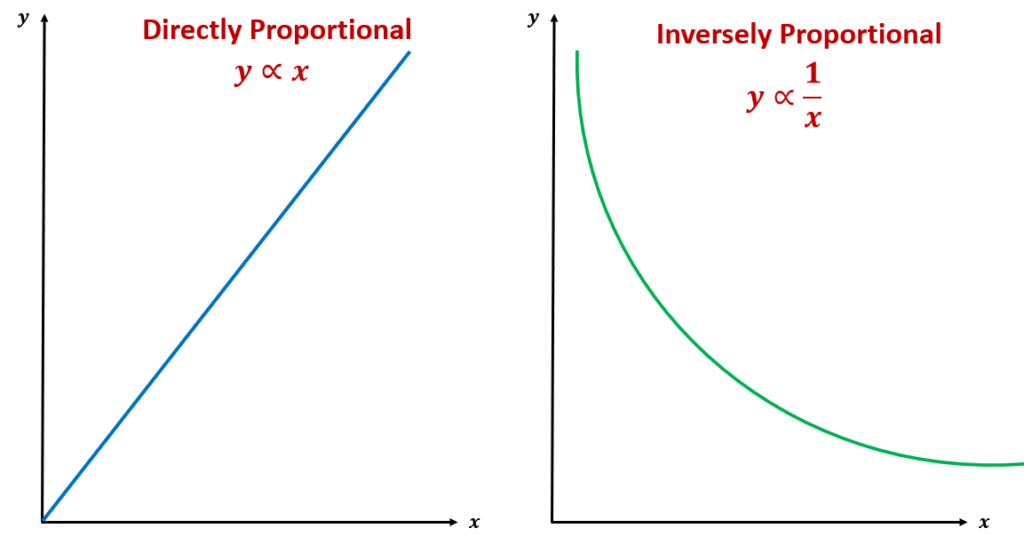
For the graph of directly proportional, it shows that as the value of x increases, the value of y increases also. We may also say that as y decreases, x also decreases. On the other hand, for the graph inversely proportional, as the value of x increases, the value of y decreases or when x decreases, the value of y increases.
Graph of Inverse Proportion
The graph below shows that the quantities are in inverse proportion. It shows the relationship between the x and y values. It reads as y is inversely proportional to x.
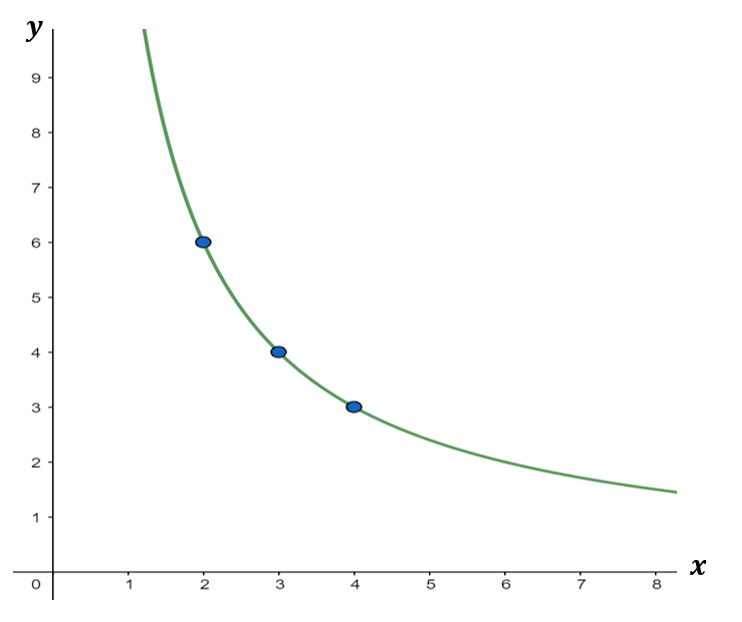
Using the graph above, let us identify some points and arrange them in a table.
| x | 2 | 3 | 4 |
| y | 6 | 4 | 3 |
Let us say that Point A has the coordinates ( 2, 6 ), Point B has the coordinates ( 3, 4 ), and Point C has the coordinates ( 4, 3 ).
By the inverse proportion formula, let us check if the graph indeed shows an inverse proportion.
| Point A: ( 2, 6 ) y=$\frac{k}{x}$ 6=$\frac{k}{2}$ 6⋅2=k 12=k k=12 | Point B ( 3, 4 ) y=$\frac{k}{x}$ 4=$\frac{k}{3}$ 4⋅3=k 12=k k=12 | Point C ( 4, 3 ) y=$\frac{k}{x}$ 3=$\frac{k}{4}$ 3⋅4=k 12=k k=12 |
Since the product of x and y is constant, the given data shows inverse proportionality with an equation y=$\frac{12}{x}$. Thus, if we want to find the values of x given y or vice versa, we can easily identify them. For example,
| when x=6 y=$\frac{12}{x}$ y=$\frac{12}{x}$ y=2 | when y=18 y=$\frac{12}{x}$ 18=$\frac{12}{x}$ x=$\frac{12}{18}$ x=23 |
Therefore, the other coordinates on the graph are ( 6, 2 ) and ( $\frac{2}{3}$, 18 ).
How Should I Write Indirect Proportion Equations?
The steps listed here should be followed when writing an inverse proportion equation.
1. Find the constant of proportionality.
2. Enter the proportionality constant into an equation after finding it.
Let us use the table below as an example and figure out its inverse proportion equation.
| x | 50 | 25 | 20 |
| y | 2 | 4 | 5 |
Using the steps mentioned above, let us write the indirect proportion equation of the given data.
1. Find the constant of proportionality.
Since the formula for indirect proportion is y=$\frac{k}{x}$, where k is the constant of proportionality, we will have,
| 2=$\frac{k}{50}$ 2⋅50=k 100=k k=100 | 4=$\frac{k}{25}$ 4⋅25=k 100=k k=100 | 5=$\frac{k}{20}$ 5⋅20=k 100=k k=100 |
The given data indeed shows an inverse proportion since the product of the shared x and y values is constant.
2. Enter the proportionality constant into an equation after finding it.
The proportion equation of the data given is:
y=$\frac{100}{x}$
Knowing the indirect proportion equation will help us to identify unknown values. For example, if y=10, then x must be equal to 10.
More Examples
Example 1
Assume that 4 people work at the same rate in painting a fence for 6 hours.
( a ) How long will it take 8 people to paint the fence?
( b ) How long will it take 12 people to paint the fence?
( c ) How many people are needed to complete the task in 30 minutes?
Solution:
This scenario shows an inverse proportion since. The painting time will go down if the number of people goes up. Let us use the inverse proportion equation,
y=$\frac{k}{x}$
where y is the number of hours spent painting the fence, x is the number of people working, and k is the constant of proportionality.
Since 4 people can paint the fence in 6 hours, we have x=4 and y=6. Plugging in these values in the equation, we have,
6=$\frac{k}{4}$
6⋅4=k
24=k
k=24
Now that we already know the constant of proportionality, which is 24, we now have the equation,
y=$\frac{24}{x}$
( a ) How long will it take 8 people to paint the fence?
Let us plug in 8 to the value of x in the equation.
y=$\frac{24}{8}$
y=3
Therefore, it will take 3 hours for 8 people to paint the fence.
( b ) How long will it take 12 people to paint the fence?
Plugging in x=12 to the inverse proportion equation we have,
y=$\frac{24}{12}$
y=2
Hence, 12 people can finish painting the fence in 2 hours.
( c ) How many people are needed to complete the task in 30 minutes?
In this question, we will use ½ or 0.5 hours since it is equivalent to 30 minutes. This time y=½, and we are solving for x.
Substituting ½ in the equation,
12=$\frac{24}{x}$
x=24⋅2
x=48
Thus, 48 people are needed to finish the task in 30 minutes.
Example 2
The value p is inversely proportional to r. If p=40 and r=2,
( a ) Find the equation relating the given data.
( b ) If p=20, what is r?
( c ) If r=5, find p.
Solution:
( a ) Find the equation relating the given data.
The statement p is inversely proportional to r is written as,
p∝$\frac{1}{r}$
To find the equation relating p and r, let us use the formula p=kr to identify the constant of proportionality.
p=$\frac{k}{r}$
40=$\frac{k}{2}$
40⋅2=k
80=k
k=80
Since we already know that 80 is the constant of proportionality, we have the equation,
p=$\frac{80}{r}$
( b ) If p=20, what is r?
Let us substitute the given value of p to the inverse proportion equation.
p=$\frac{80}{r}$
20=$\frac{80}{r}$
r=$\frac{80}{20}$
r=4
Therefore, the value of r is equal to 4 when p is 20.
( c ) If r=5, find p.
This time, r is given, and we must find the value of p.
p=$\frac{80}{5}$
p=16
Hence, when r=5, the value of p is 16.
Example 3
Suppose it takes 3 students to finish a project in 6 hours. When 9 students are working on the same project, how long does it take to complete the task?
Solution:
Let x=number of students and y=hours spent doing the project.
Let us first find the constant of proportionality. Thus, we have
y=$\frac{k}{x}$
6=$\frac{k}{3}$
6⋅3=k
18=k
k=18
Hence, the inverse proportion equation to represent the scenario is,
y=$\frac{18}{x}$
Since k=18, let us now solve for hours spent in doing the project if 9 students will be working on it.
y=$\frac{k}{9}$
y=2
Therefore, it will take 2 hours to finish the project by 9 students.
Example 4
Suppose the table below shows an inverse proportion.
| x | 5 | 4 | 3 | |
| y | 10 | 12 | 20 |
( a ) Find the constant of proportionality
( b ) Write the equation of inverse proportion
( c ) Complete the table.
Solution:
The table has given the values for x and y. Since they are inversely proportional, we may have the equation,
y=$\frac{k}{x}$
( a ) Find the constant of proportionality
Let us find the constant of proportionality from the table where both x and y are given.
| y=$\frac{k}{x}$ 12=$\frac{k}{5}$ 12⋅5=k 60=k k=60 | y=$\frac{k}{x}$ 20=$\frac{k}{3}$ 20⋅3=k 60=k k=60 |
Hence, the constant of proportionality is 60.
( b ) Write the equation of inverse proportion.
By substituting the computed constant of proportionality, the equation is,
y=$\frac{k}{x}$
( c ) Complete the table.
Here is the complete table.
| x | 6 | 5 | 4 | 3 |
| y | 10 | 12 | 15 | 20 |
When y=10,
y=$\frac{60}{x}$
10=$\frac{60}{x}$
x=$\frac{60}{10}$
x=6
When x=4,
y=$\frac{60}{x}$
y=$\frac{60}{4}$
x=15
Example 5
m is inversely proportional to n. When m=4, n=6.
Draw the graph after filling out the values in the table below.
| n | 2 | 3 | 4 | 6 | 8 | 9 |
| m | 6 |
Solution:
Since m is inversely proportional to n, in symbols, it is written as m∝$\frac{1}{n}$.
Let us use the given values of n and m to find the constant of proportionality. Hence, we will use the formula,
m=$\frac{k}{n}$
Substituting the given values, we have,
6=$\frac{k}{4}$
6⋅4=k
24=k
k=24
Knowing the value of the constant of proportionality makes it easy to complete the data.
We will now utilize the equation m=$\frac{24}{n}$.
| when n=2 m=$\frac{24}{n}$ m=$\frac{24}{2}$ m=12 | when n=3 m=$\frac{24}{n}$ m=$\frac{24}{3}$ m=8 | when n=6 m=$\frac{24}{n}$ m=$\frac{24}{6}$ m=4 |
| when n=8 m=$\frac{24}{n}$ m=$\frac{24}{8}$ m=3 | when n=9 m=$\frac{24}{n}$ m=$\frac{24}{9}$ m=$\frac{8}{3}$ |
The table below shows the completed data.
| n | 2 | 3 | 4 | 6 | 8 | 9 |
| m | 12 | 8 | 6 | 4 | 3 | $\frac{8}{3}$ |
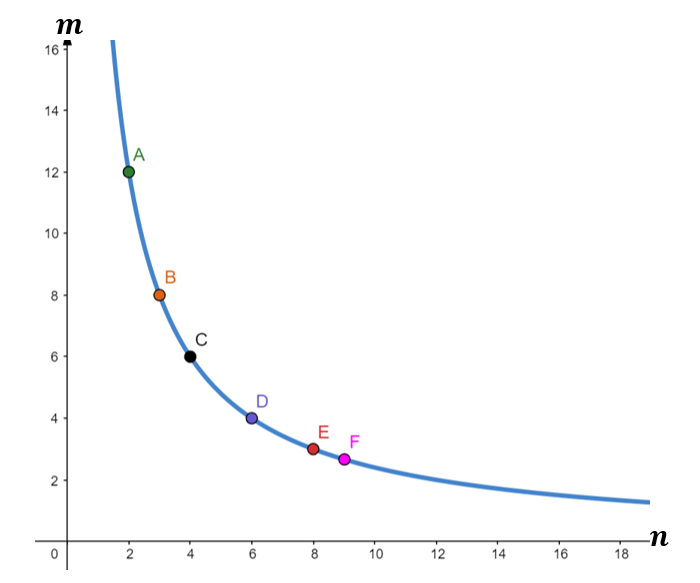
Let us write each pair as coordinates of points A, B, C, D, E, and F. Hence, we may have,
Point A ( 2, 12 )
Point B ( 3, 8 )
Point C ( 4, 6 )
Point D ( 6, 4 )
Point E ( 8, 3 )
Point F ( 9, $\frac{8}{3}$ )
The figure below shows the graph of m=$\frac{24}{n}$.
Summary
Definition: Two quantities are said to be in inverse proportion when one quantity increases while the other decreases and vice versa.
Formula:
y=$\frac{k}{x}$
k is the constant of proportionality
As x decreases, y increases.
As x increases, y decreases.
How do I Write inverse proportion Equations?
The steps listed here should be followed when writing an inverse proportion equation.
1. Find the constant of proportionality.
2. Enter the proportionality constant into an equation after finding it.
Frequently Asked Questions on Inverse Proportion (FAQs)
What is meant by inverse proportion?
One kind of proportionality relationship is inverse proportion. There is an inverse proportionality in two quantities when one quantity’s value increases relative to a decrease in another or vice versa.
Other names for inverse proportion include indirect proportion and inverse variation. Examples of inverse proportion include the amount of time it takes to travel a certain distance lowers as our speed rises, and the time it takes to finish a task decreases as more people work on it.
How do the inverse and direct proportions differ from one another?
Direct proportion and inverse proportion are the two main types of proportionality. To illustrate how the amounts and quantities relate to one another, a direct and inverse proportion is used. The symbol is used to denote proportionality.
y∝x is read as “y is directly proportional to x”.
y∝$\frac{1}{x}$ is read as “y is inversely proportional to x”.
Direct Proportion
When y∝x, two variables x and y are said to be in direct proportion. This suggests that, for a constant k, y = kx. The ratio of two variables in a direct variation relationship is equal for all values.
Inverse Proportion
When y∝1/x, two variables, x and y, are said to be in inverse proportion. This means that, for a constant k, y = k/x. The product of two variables in an inverse proportion relationship is equal for all values.
What is the equation for inverse proportion?
The equation for inverse proportion is y=$\frac{k}{x}$ or xy=k, where k is the constant of proportionality. You can use the known values to get the value of the constant k and then apply this formula to determine all the other unknown values.
How do you find the value of “k” in an inverse proportion?
The variable “k” is the constant of proportionality. In inverse proportion, we follow the formula y=$\frac{k}{x}$ when y is inversely proportional to x. Hence, to find the value of “k”, you must get the product of the given values of x and y.
Let us say, for instance, that y is inversely proportional to x, and we know that x=5 and y=6. Here is how to find the constant of proportionality, “k”.
k=xy
k=5⋅6
k=30
Hence, the constant of proportionality for the inverse proportion is 30. The equation that represents the given value is,
y=$\frac{30}{x}$
Finding the value of the constant of proportionality is very helpful for solving the equation for the inverse proportion and for determining other values. Therefore, we can readily determine y as 3 or 2, respectively, if x is 10 or 15.
Recommended Worksheets
Inverse Proportion (Summer Themed) Math Worksheets
Direct Proportion (Labor Day Themed) Math Worksheets
Proportion (Thanksgiving Day Themed) Math Worksheets









