Introduction
One fundamental concept in mathematics is the equation of a straight line that represents a straight line on a Cartesian plane using algebraic expressions. This concept is essential for understanding various algebra, geometry, and calculus topics. In this article, we will cover different ways to write or express the equation of a straight line, as well as its applications and related concepts.
Grade Appropriateness
The equation of a straight line is typically introduced to students in middle school, around 7th or 8th grade. However, the concept becomes more relevant and in-depth in high school, specifically in Algebra I and Geometry courses.
Math Domain
The equation of a straight line falls under the Algebra and Geometry domains in mathematics.
Applicable Common Core Standards
The equation of a straight line is covered in the following Common Core Standards for Mathematics:
CCSS.MATH.CONTENT.8.EE.B.5 (Grade 8)
CCSS.MATH.CONTENT.HSA.REI.D.10 (High School: Algebra)
CCSS.MATH.CONTENT.HSG.GPE.B.5 (High School: Geometry)
Definition of the Topic
A straight line is a set of points in which every point on the line segment joins any other point on the line. To begin, visualize a straight line that connects the points in the following list.
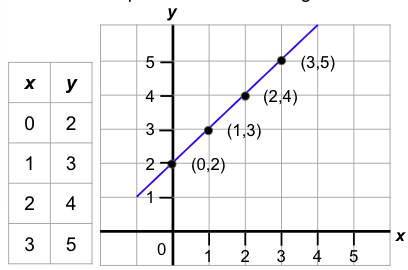
A mathematical expression known as the equation of a straight line describes the relationship between the coordinates of points on a straight line in a Cartesian plane. There are several forms of the equation of a straight line, including the slope-intercept form, point-slope form, and standard form.
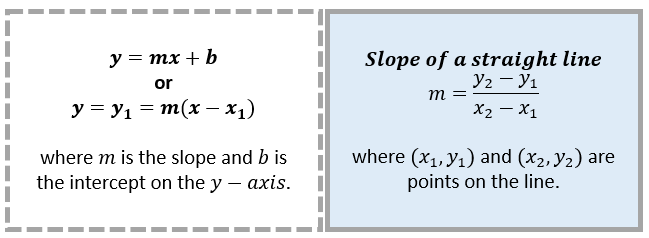
Key Concepts
Slope: The slope is the measure of the steepness of a line, represented as the ratio of the change in the y-coordinates (y – y1) to the change in the x-coordinates (x – x1) between two points on the line.
Y-intercept: The point where the line intersects the y-axis is known as the y-intercept.
Slope-intercept form: The slope-intercept form has the equation y = mx + b, where m represents the slope and b represents the y-intercept.
Point-slope form: The point-slope form has the equation y – y1 = m(x – x1), where the line’s slope is m, and the point on the line is (x1, y1).
Standard form: The equation of a straight line in the form Ax + By = C, where A and B cannot be both equal to zero.
Discussion with Illustrative Examples
Example 1: Slope-intercept form
Find the equation of a line with a slope of 2 and a y-intercept of -3.
Solution
The slope-intercept form is y = mx + b, so we plug in the values: y = 2x – 3.
Example 2: Point-slope form
Find the equation of a line with a slope equal to 3 and passes through the point (4, -2).
Solution
Point-slope form: y – y1 = m(x – x1).
Given: x1 = 4, y1 = -2, and m = 3
Plug in the values: y – (-2) = 3(x – 4).
Simplify: y + 2 = 3x – 12.
Examples with Solutions
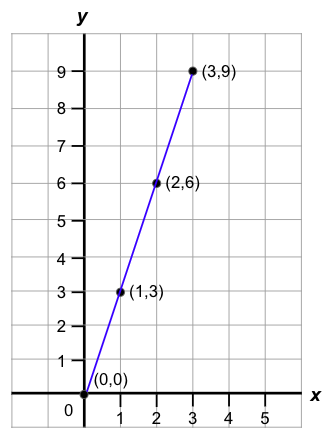
Example 1
Consider the equation y = 3x for a straight line. To draw its line, we must first calculate certain numbers. Determine the y-values of each coordinate. Substitute the x-values.
y1 = 3 (0) = 0
y2 = 3 (1) = 3
y3 = 3 (2) = 6
y4 = 3 (3) = 9
| x | 0 | 1 | 2 | 3 |
| y | 0 | 3 | 6 | 9 |
Example 2
Determine the equation of the line with a slope equal to 3, and the line passes through (4, 1).
Using y – y1 = m ( x – x1 ) with m =3, x1 = 4 and y1 = 1:
y – 1 = 3 (x – 4)
y – 1 = 3x – 12
y = 3x – 12 +1
y = 3x – 11
Example 3
Find the slope.
a. (2,1),(0,0)
b. (4,5),(6,2)
c. (3,8),(7,3)
d. (1,0),(4,2)
Solution
Using m=$\frac{y_2-y_1}{x_2-x_1}$, we have,
a. m=$\frac{0-1}{0-2}$=$\frac{1}{2}$
b. m=$\frac{2-5}{6-4}$=-$\frac{3}{2}$
a. m=$\frac{3-8}{7-3}$=-$\frac{5}{4}$
a. m=$\frac{2-0}{4-1}$=$\frac{2}{3}$
Example 4
Work out the equation of a line in standard form with a slope of m = 1/2 and a y-intercept of 3.
Solution
Let us use the slope-intercept form to find the equation of the line since we know that m = ½ and y-intercept of 3,
y = ½ x + 3
An equation in standard form is written in the form Ax + By = C; therefore, manipulating the equation, we have,
y=½x+3
2(y=½x+3)2
2y=x+6
-6=x-2y
x-2y=-6
Example 5
Work out the equation of a line parallel to the line y = 2x + 1 and passes through the point (-1,1).
Solution
Parallel lines share the same gradient or slope and are in the same plane but do not intersect.
To find the equation of the line parallel to y = 2x + 1 and passes through (-1,1), we’ll use the point-slope form y – y1 = m (x – x1). Substituting the same slope, m = 2, and the coordinates x1 = -1, and y1 = 1, we have,
y – 1 = 2 ( x – (-1) )
y – 1 = 2 ( x + 1 )
y – 1 = 2x + 2
y = 2x + 3 (Slope-intercept Form)
What if we want to find the equation of the line perpendicular to y = 2x + 1 and passes through the point ( -1, 1 )?
Lines in the same plane with slopes that are negative reciprocals or opposite reciprocals are said to be perpendicular. Hence, the product of their slopes is equal to -1.
Since the slope of y = 2x + 1 is m=2, the slope of the line perpendicular to it is m⊥=-½.
m⋅m⊥=2⋅-½=-1
Using the point-slope form and plugging m=-½, and the coordinates x1 = -1, and y1 = 1, we have,
y-1=-½ (x-(-1))
y-1=-½(x+1)
2y-2=-(x+1)
2y-2=-x-1
x+2y=2-1
x+2y=1 (Standard Form)
Therefore, line y = 2x + 1 and passes through the point (-1,1) is parallel to y = 2x + 3 and perpendicular to x+2y=1.
Real-life Application with Solution
Example: A car rental company charges a flat fee of $20 and an additional $0.15 per mile driven. Find the equation representing the cost (y) as a function of the distance traveled in miles (x).
Solution: Since the cost is a linear function of miles driven, we can use the slope-intercept form, y = mx + b. In this case, the slope (m) represents the cost per mile ($0.15), and the y-intercept (b) represents the flat fee ($20). So, the equation is y = 0.15x + 20.
Practice Test
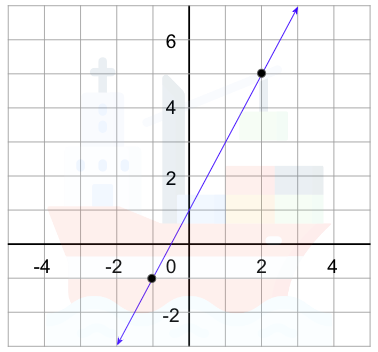
1. Find the Slope of the line.
2. Find the equation (slope-intercept form) of the line passing through the points (3, 5) and (7, 9).
3. Find the point-slope form of the equation of a line with a slope of -4 and passing through the point (2, 8).
4. Given the equation 3x – 2y = 6, find the slope and y-intercept.
5. Determine the equation of the line perpendicular to the line y = -3x + 2 and passing through the point (3, 7)?
6. Determine whether the lines with equations 2x + 3y = 6 and 6x – 4y = 12 are parallel, perpendicular, or neither.
Frequently Asked Questions (FAQs)
Can a vertical line be represented by an equation in slope-intercept form?
No, a vertical line has an undefined slope and cannot be represented by the slope-intercept form. However, it can be represented by an equation in the form x = k, where k is the x-intercept.
What is the slope or gradient of a horizontal line?
A horizontal line has a slope equal to zero, as there is no change in the y-coordinates between any two points on the line.
How can I determine if two lines are parallel?
Two lines are considered to be parallel if they have different y-intercepts but the same slope.
How can I determine if two lines are perpendicular?
Two lines on the same plane are perpendicular if the product of the slopes is negative one (-1).
Can a line have more than one equation?
Yes, a line can have multiple equivalent equations in different forms, such as slope-intercept, point-slope, and standard form. These equations can be transformed from one form to another using algebraic techniques.
Recommended Worksheets
Equation of a Straight Line (National Maritime Day Themed) Math Worksheets
Horizontal and Vertical Line (Women’s History Month Themed) Math Worksheets
Linear Equation (National Beverage Day Themed) Math Worksheets









