Slope of a Line

Definition

The slope of a line describes the relationship between the change in horizontal and vertical positions of a point as it goes through the line.

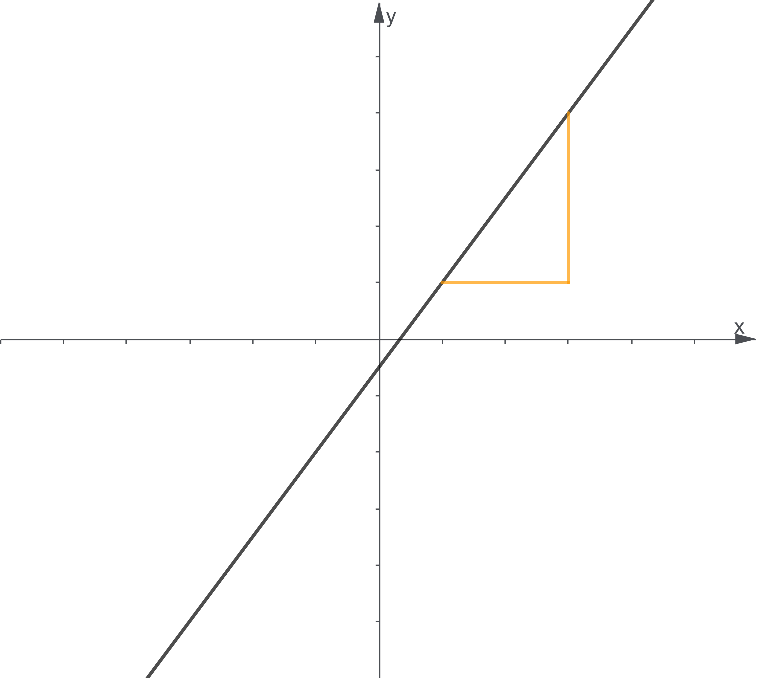
We can think of it intuitively as how steep a line is. The larger the slope, the steeper the graph of the line becomes. This steepness is defined by how much distance a point rises to another point over how much it runs through the line.

Imagine if we drop a ball down that line. If the line is almost flat, we do not expect the ball to roll as much. However, as we slowly replace the line each time with a steeper one, we can observe that the ball rolls faster as the steepness of the line increases. In this regard, we get a gist of how the concept of the slope is relevant for us. 

Mathematically speaking, the slope of a line can be defined as the ratio between the difference in the vertical coordinates over the difference in the horizontal coordinates of any two points in the line. We shall later discuss this in detail.

Additionally, this quantity tells us the direction of a line. Whether the graph is an increasing diagonal line, a decreasing diagonal line, a flat horizontal line, or a flat vertical line, the slope can tell us how the line looks without having to visualize its graph.

Slope Formula

We now introduce in the succeeding parts an important set of topics covering the formula for solving the slope of a line, how it is derived and used, and how we can interpret the result we obtain from the formula.

Derivation of the Slope Formula

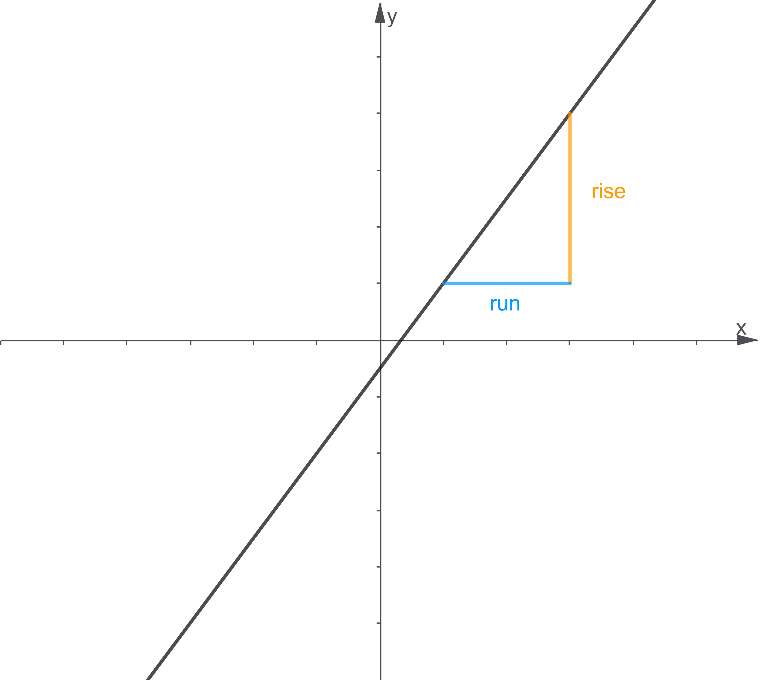
We revisit the graph of the line that we have first encountered. From its intuitive sense, the slope can be measured as the rise of a line from on point to another over how long the line runs between them. As such, we write a basic, intuitive formula for the slope:

Slope=$\frac{rise}{run}$

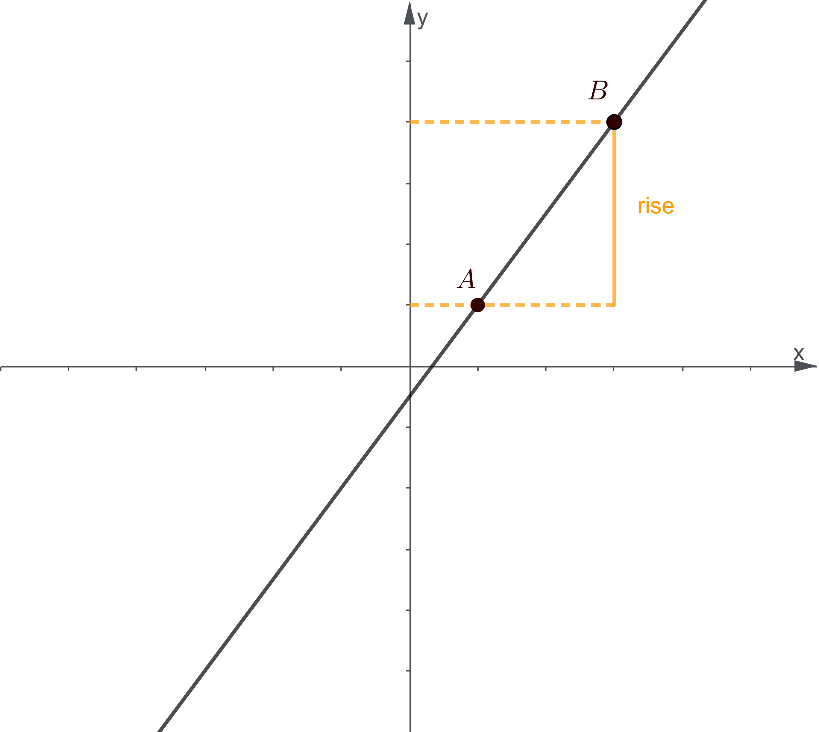
We can define how the line “rises” by taking the vertical distance between the two points. For two points A and B, their vertical distance is given by:

rise=(y coordinate of 2nd point)-(y coordinate of 1st point)

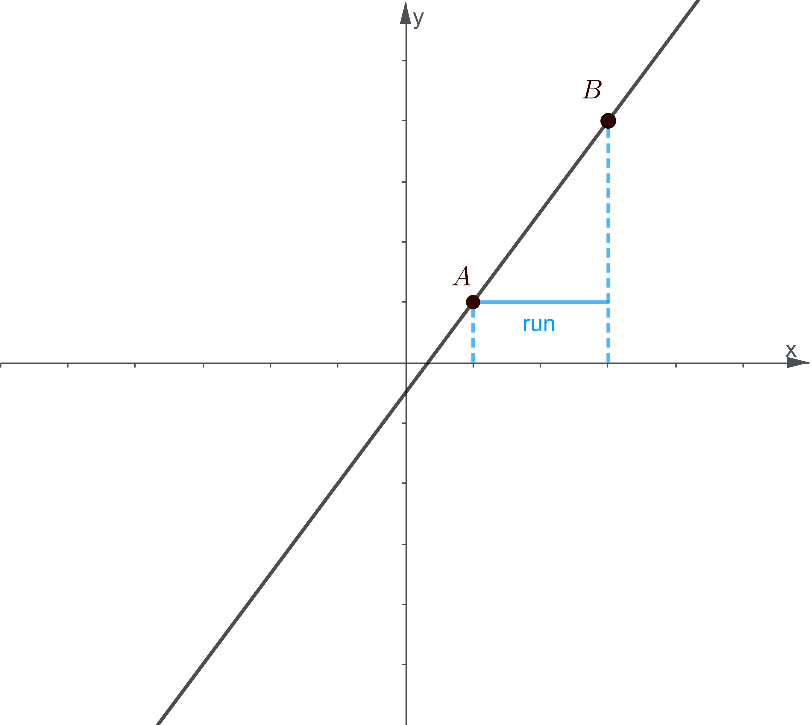
Likewise, we further describe how the line “runs” by taking the horizontal distance between the two points. This can be defined as follows:

run=(x coordinate of 2nd point)-(x coordinate of 1st point)

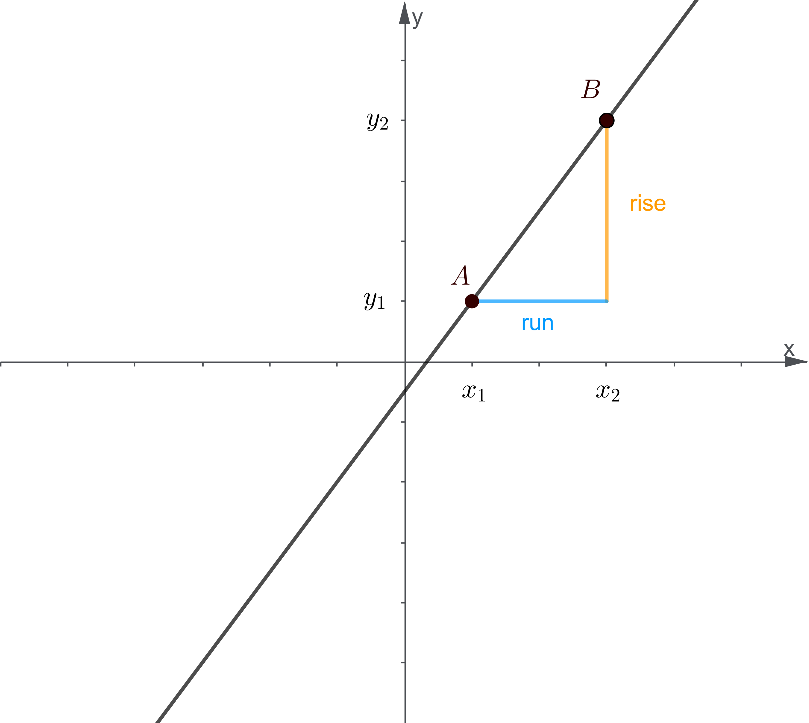
Going back to our basic slope formula, we expand the initial formula to include our observations so far about the rise and the run of the line:

Slope=$\frac{(y\: coordinate\: of\: 2nd\: point)-(y\: coordinate\: of\: 1st\: point)}{(x\: coordinate\: of\: 2nd\: point)-(x\: coordinate\: of\: 1st\: point)}$

By assigning variables x₁, x₂, y₁, y₂ to the equation, we finally arrive at the Slope Formula:

m=$\frac{y_2-y_1}{x_2-x_1}$

What is the Slope Formula?

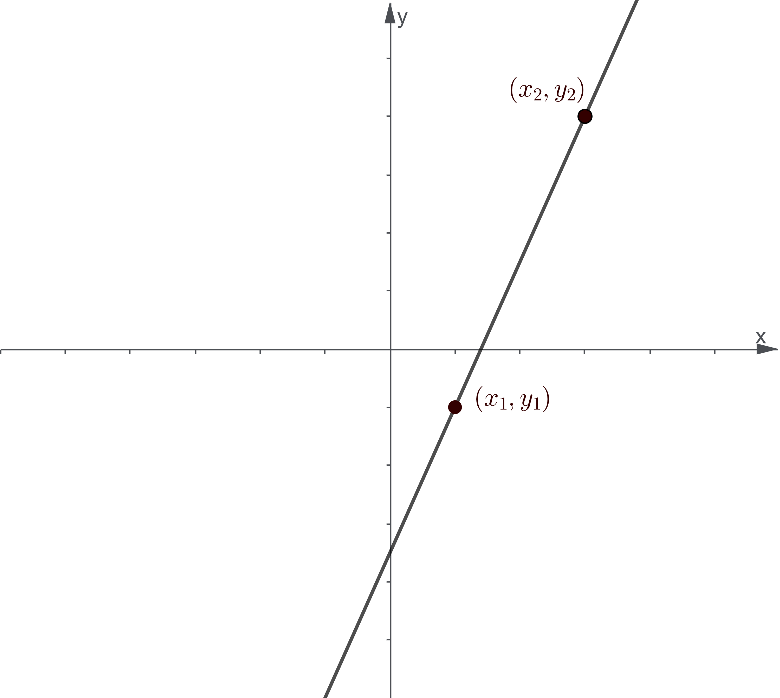
From the previous derivation we performed, the formula used in computing for the slope of a line is given by:

m=$\frac{y_2-y_1}{x_2-x_1}$

where m is the slope of the line, (x₁, y₁) is the position of the first point on the coordinate plane, and (x₂, y₂) is the position of the second point on the coordinate plane.

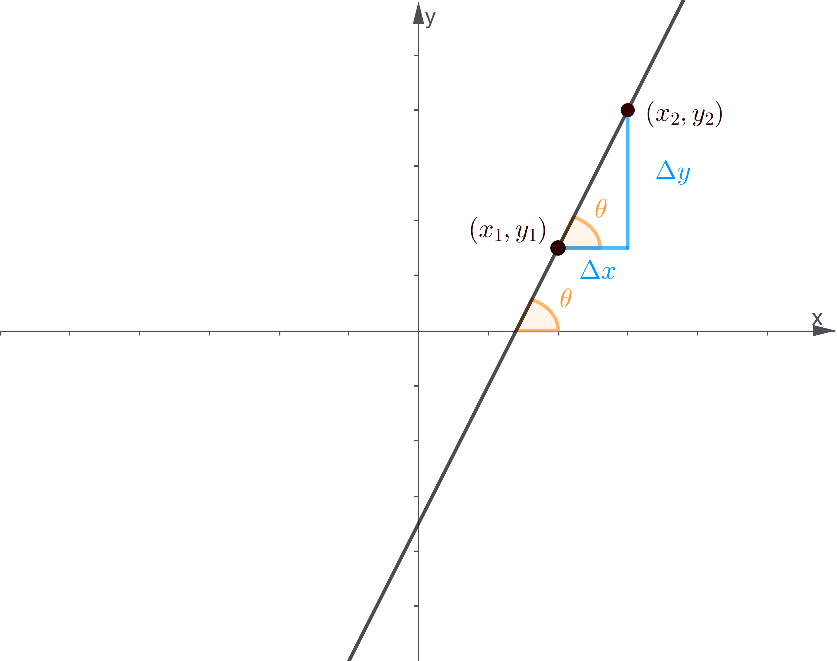
Alternatively, we can make use of the graphical information to produce another formula involving the angle a line forms on the x-axis:

m=tan⁡(θ)=$\frac{△y}{△x}$

From Trigonometry, the tangent function relates the slope of a line to the change in x and y coordinates, denoted by x and y, and the angle of inclination formed between the x-axis and the line.

It is interesting to note that both forms of the equation are valid, since they both follow the definition of the slope. In fact, we can extend the formula to include both ways in solving for the slope:

m= tan⁡(θ)=$\frac{y_2-y_1}{x_2-x_1}$

How is it used?

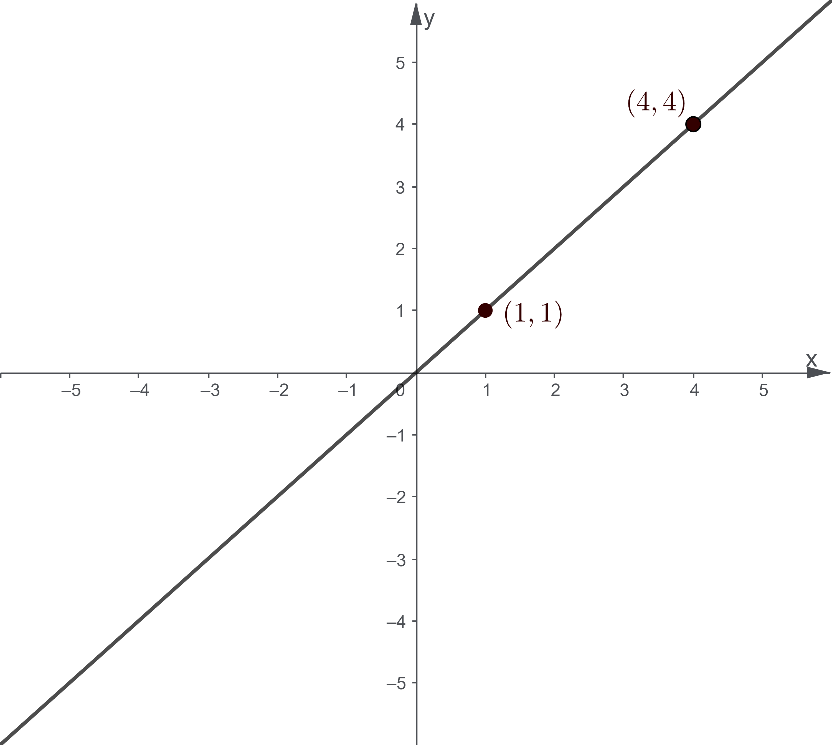
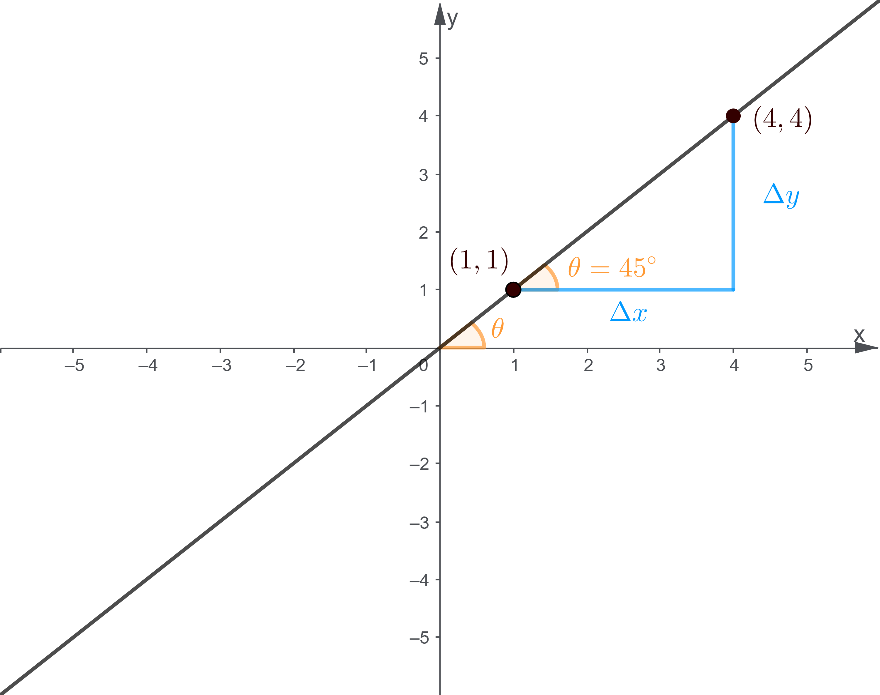
As a practice on how we apply the slope formula, let us work together on an example where the graph of a line is shown below:

To get the slope of a line, we pick two points on the line and determine their coordinates. In this example, we choose Point A located at (1,1) and Point B which is located at (4,4). 

As a recall to previous geometry lessons, Point A is located 1 unit to the right of the origin and then 1 unit upwards. Therefore, its coordinates are given by A(1,1). In a similar manner, Point B is located 4 units to the right of the origin and then 4 units upwards. Hence, its coordinates are given by B4,4. 

We then substitute the coordinates of first point A x₁=1 and y₁=1 to the formula. Similarly, we substitute the coordinates of second point B x₂=4 and y₂=4:

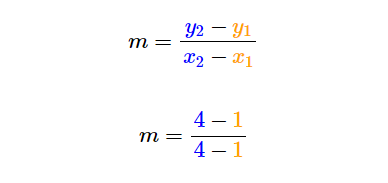
Next, we take the difference between the y-coordinates on the numerator and the x-coordinates on the denominator. This leads us to simplify the expression to a fraction (3/3).

Finally, we take the ratio between the numerator and the denominator to obtain the value of the slope. In this example, the value of the slope is computed to be m=1.

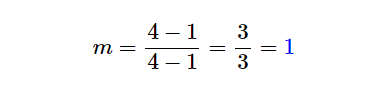
We might ask: “Which point goes in the formula first? Which point goes last?” The answer is: either point could be used as the first or last point in the formula. The order in which points are chosen will not affect the slope of the line as long as we make sure the substitution remains consistent. We use the previous example to prove this observation.

Suppose we choose point B as the first point and point A as the second point. Substituting the coordinates of point B, we have x₁=4 and y₁=4. Moreover, we have x₂=1 and y₂=1 from the coordinates of point A.

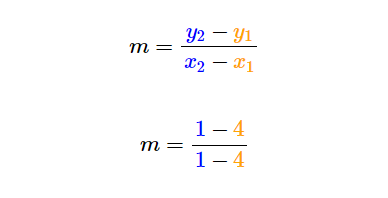
Taking the difference between the x and y coordinates on the numerator and denominator respectively, we observe that from (3/3) the sign of both numerator and denominator becomes inverted into (-3/-3).

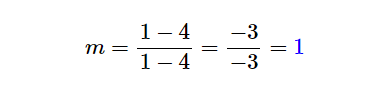
However, when we take the quotient of the numerator over the denominator, we arrive at the same slope value m=1. Therefore, we have shown both methods result to the same correct slope of the line.

Next, we practice how to use the tangent function to solve for the slope of a line. We use the same graph as the previous example, with the angle of inclination given by θ=45°:

Since the value of is given, we can directly substitute the angle to the trigonometric function to solve for the slope of the line:

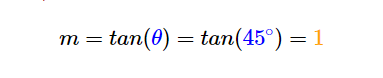
Comparing the results obtained from using two points and the tangent function, we have shown that both approaches give the correct slope of the line. The approach would simply depend on what information is available or given to us.

Slope of One Line

Earlier, we have mentioned that the slope determines the direction of a line. Now that we know how to solve for the slope of a line, we can think about how this value could be interpreted:

Slope of a Diagonal Line

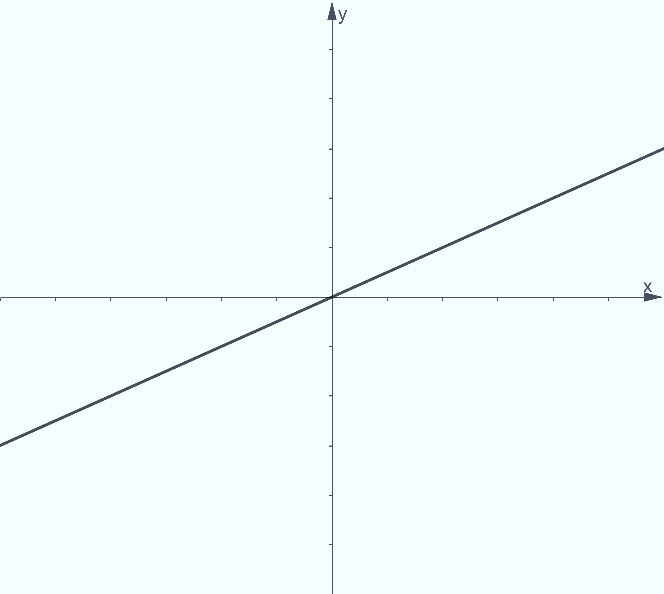
A positive slope m>0 implies that the line is increasing. This means that the line goes higher up in the y-direction as it travels farther away in the x-direction. This can be illustrated by an increasing diagonal line.

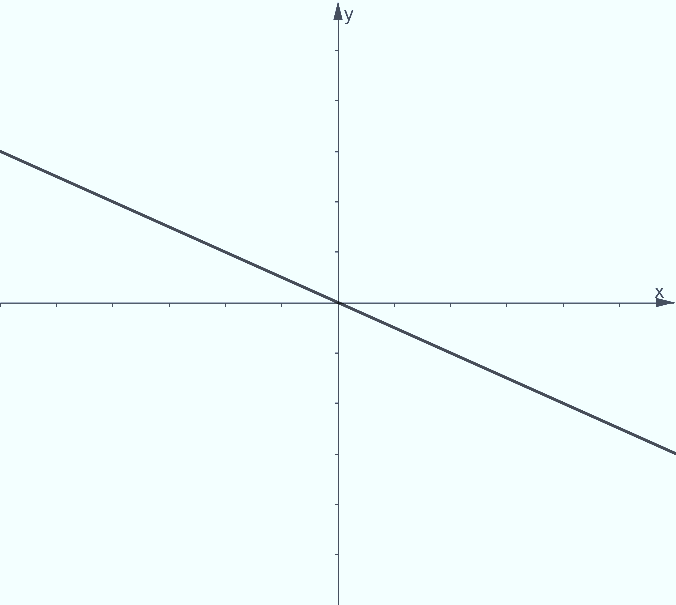
On the other hand, a negative slope m<0 implies that the line is decreasing. This means that the line goes down contrary to the direction when the slope is positive. This can be illustrated by a decreasing diagonal line. 

Slope of a Horizontal Line

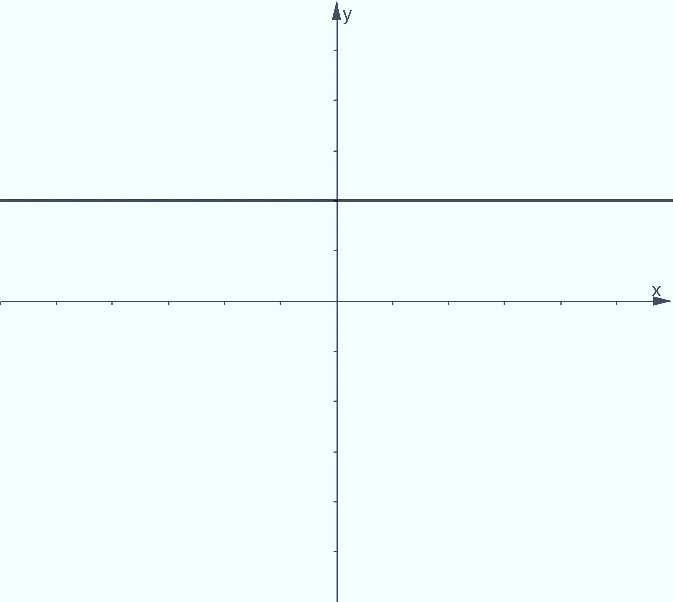
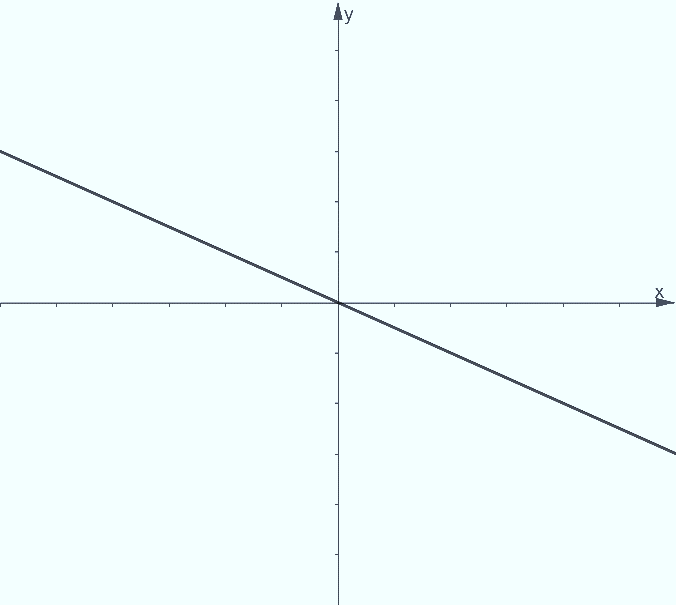
A slope of zero value m=0 implies that the line is constant in the y-axis. This means that it neither increases nor decreases as it travels through the x-direction. Graphically, this represents a flat horizontal line.

Slope of a Vertical Line

Lastly, an undefined slope implies that the line is constant in the x-axis. This means that the line remains in one x-coordinate as it travels through the y-direction. This can be illustrated by a flat vertical line.

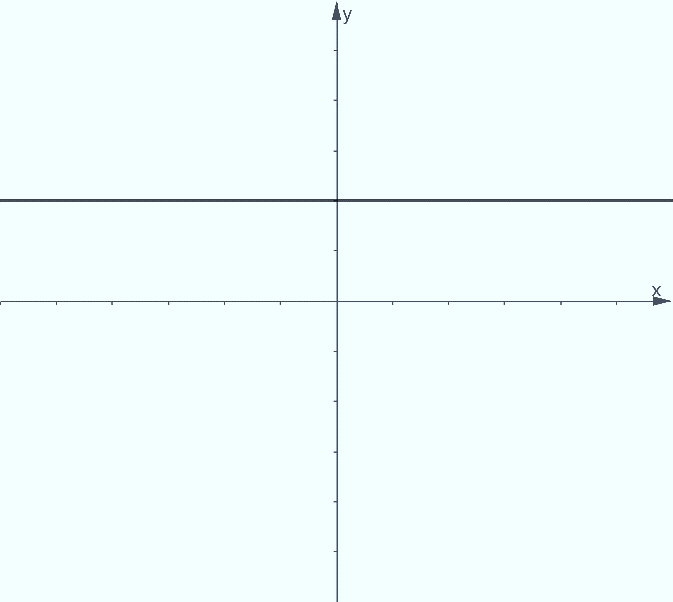
So, when do we expect the slope value to be undefined? An undefined slope occurs when we observe no change in the horizontal distance between two points in a line. Since the two points share the same x-coordinate, applying the slope formula will give us this scenario:

Since the denominator becomes zero, the ratio becomes undefined and thus an undefined slope is obtained as we cannot divide a number by zero.

Slope of Two Lines

We have explored the slope values of a single line so far. Can we determine the slope of more lines? Turns out, we can also apply Geometry to get the slope of another line if the slope of one line is known.

Slope of Two (or More) Parallel Lines

Suppose we have two parallel lines l₁ and l₂, whose graphs are shown below:

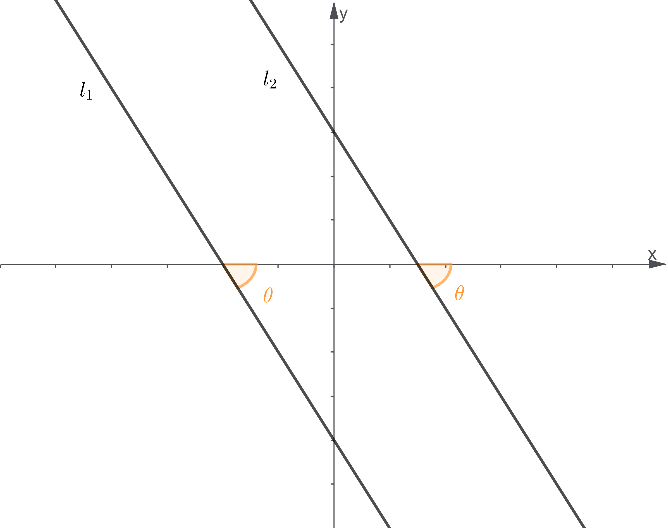
If l₁ forms an angle – with the x-axis, then the slope of l₁ can be expressed as follows:

m₁=tan⁡(-θ)

Moreover, since l2 is parallel to l1, then the second line must also form an angle – with the x-axis. It follows that the slope of l2 can be expressed as follows:

m₂=tan⁡(-θ)

Therefore, we conclude that their slopes are equal:

m₁=m₂

In general, we can make the following observation:

For two (or more) parallel lines, their slopes are equal.

Slope of Two Perpendicular Lines

Suppose we then have two perpendicular lines, l₃ and l₄, whose graphs are shown below:

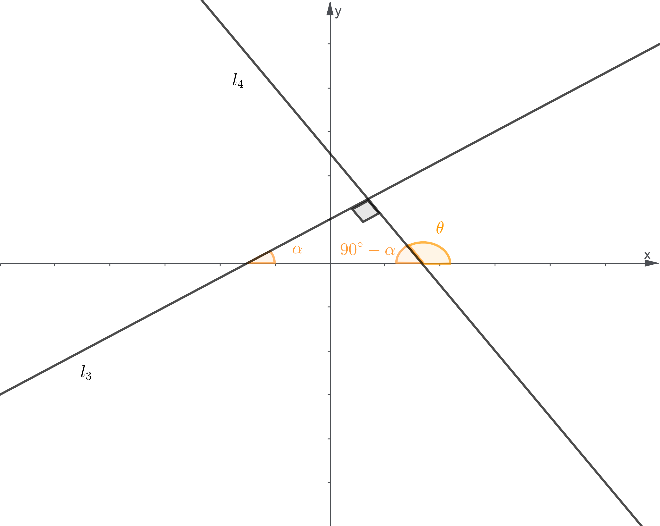
Since lines l₃ and l₄ are perpendicular to each other, their intersection forms a right angle. Consequently, by the properties of perpendicular angles we can relate the angles and as follows:

α=90°+θ

If the slopes of lines l₃ and l₄ are given by the tangent of their angles of inclination and , then we have the following equations for their slopes m₃ and m₄:

m₃=tan⁡(α), m₄=tan⁡(θ)

We can expand the expression for using the relationship between the two angles:

m₃=tan⁡(90°+θ)

Using the trigonometric identity tantan (90°+θ) =-cot⁡(θ), we can rewrite the slope m₃ as:

m₃=-cotcot (θ) =-$\frac{1}{tan⁡(θ)}$

Therefore, by substituting m₄ we can relate the slopes of both perpendicular lines:

m₃=-$\frac{1}{m_4}$

In general, we can make the following observation:

For two perpendicular lines, their slopes are negative reciprocals of each other.

Slope Equations

Aside from the slope formula, the slope of a line also has its applications in linear equations. Based on the given quantities, we can predict the behavior of a line using slope equations.

There are two types of line equations involving the slope of a line: the point-slope equation of a line, and the slope-intercept equation of a line.

Point-Slope Equation

The point-slope equation of a line is given by:

y₂-y₁=m(x₂-x₁)

This equation relates the coordinates of two points in a given line to its slope. In the above equation, m denotes the slope of the line, and the x and y coordinates are taken from the two points (x₁, y₁) and (x₂, y₂) used to measure the slope. Note that if we divide both sides of the equation by (x₂-x₁), we can derive the slope formula from the point-slope equation.

This equation becomes handy if we know at least one point and the slope, and we need to know the position of another point that lies in the line.

Slope-Intercept Equation

On the other hand, the slope-intercept form can be treated as a special case of the point-slope equation. As proof, a quick derivation is shown below.

Suppose we have one point located at (x,y). If one point lies on the y-axis, then it x-coordinate must be 0. Hence, we can write the coordinates of the y-intercept as (0,b). Applying the Point-Slope Equation, we have:

y-b=m(x-0)

Simplifying the equation, we can rewrite the equation to a compressed form:

y-b=mx

∴y=mx+b

Here, m denotes the slope of the line, the point (x,y) is used as one point for measuring the slope, and b denotes the y-coordinate at the point where the line intersects the y-axis.

Problem-Solving Examples

We can now proceed to solving sample problems to apply what we have learned so far. Each problem tackles the different formulas and equations discussed and gives us a challenge on how to navigate with the information given to us.

Using Slope Formula

Sample Problem 1:

From the graph shown below, we have a line and points C and D whose coordinates are not given. We are then asked the following questions:

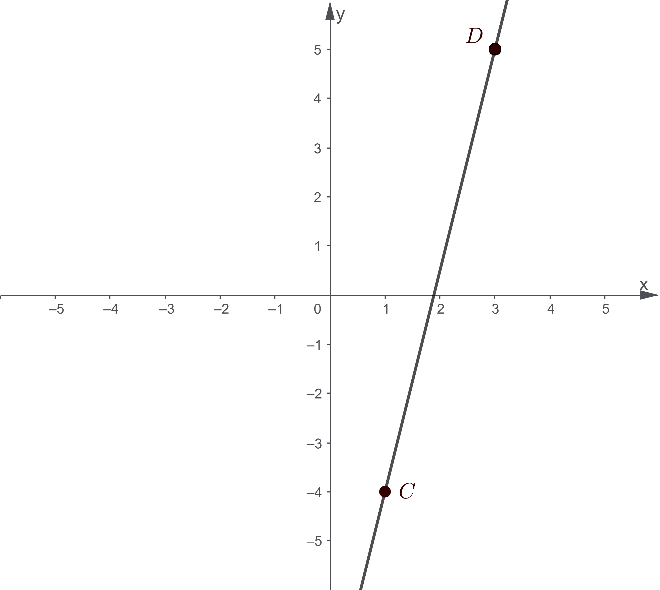
1. What are the coordinates of Point C and Point D?

We note that the given graph has a known grid. By inspecting the graph visually, we can locate Point C. From the origin, Point C is located 1 unit to the positive x-direction, then 4 units down to the negative y-direction. Hence, we conclude that Point C is located at (1,-4).

Then, we locate Point D. From the origin, Point C is located 3 units to the positive x-direction, then 5 units up to the positive y-direction. Hence, we conclude that Point D is located at (3,5).

2. What is the difference between the y-coordinates of points C and D?

Since the y-coordinate of Point C is y₁=-4 and the y-coordinate of Point D is y₂=5, we can then solve for the difference using:

y₂-y₁=5-(-4)=9

3. What is the difference between the x-coordinates of points C and D?

Since the x-coordinate of Point C is x₁=1 and the x-coordinate of Point D is x₂=2, we can then solve for the difference using:

x₂-x₁=3-1=2

4. What is the slope of the line, using points C and D?

We recall the Slope Formula is given by:

m=$\frac{y_2-y_1}{x_2-x_1}$

We can then substitute the previously computed differences into the formula to solve for the slope of the line, using points C and D:

m=$\frac{9}{2}$=4.5

Sample Problem 2:

We consider the same graph used in Sample Problem 1. Suppose we have a third point B in the same line, located at 2, 0.5. We are then asked the following questions:

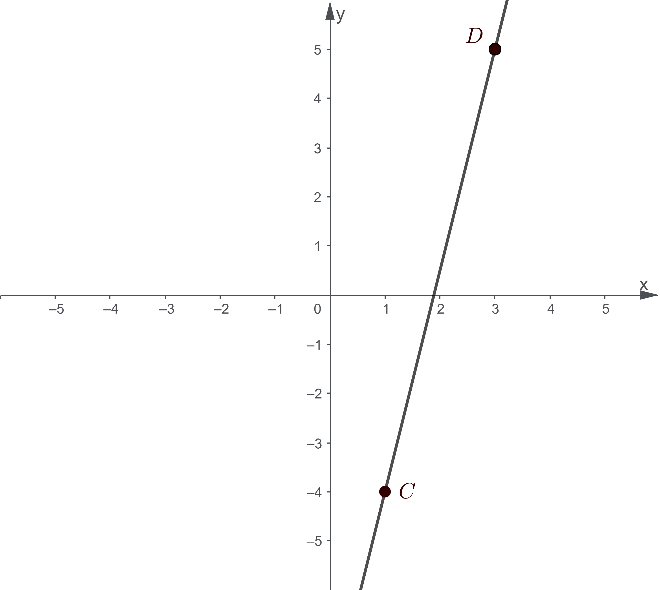
1. What is the slope of the line, using points D and C?

We recall that the order of the points used in the Slope Formula gives the same result. Therefore, we conclude from previous computations in Sample Problem 1 that the slope is m=4.5.

2. What is the slope of the line, using points B and D?

Since the y-coordinate of Point B is y₁=0.5 and the y-coordinate of Point D is y₂=5, we can then solve for the difference using:

y₂-y₁=5-0.5=4.5

Similarly, the x-coordinate of Point B is x₁=2 and the x-coordinate of Point D is x₂=3, we proceed to solve for the difference using:

x₂-x₁=3-2=1

Hence, by applying the Slope Formula we can solve for the slope of the line using points B and D:

m=$\frac{4.5}{1}$=4.5

We observe that the same slope is obtained even if a separate set of points is used. This observation holds true for any two points in the same line.

3. What is the slope of the line, using points B and C?

From the previous observation, we know that the same slope will be obtained if we compute for the slope using points B and C. Hence, we conclude that the slope of the line is also m=4.5.

4. Suppose we add two lines l₁ and l₂ to the graph. If both lines are parallel to the line formed by points C and D, what would be the slope of these lines?

We recall that for all parallel lines, they must share the same slope. Thus, we can say that the slopes of lines l₁ and l₂ are equal to:

m₁=m₂=4.5

Sample Problem 3:

In a rectangular sandbox, a blue marble is located at the center. A boy threw a green marble into the sandbox, and it landed near the blue marble. Afterwards, the boy used a ruler to measure the distance between the marbles and he got the following measurements:

If the boy wishes to draw a straight line connecting the two marbles, what would be the slope of the line he will draw?

Since the horizontal and vertical distances are known to us, we can use the alternative Slope Formula to solve for the slope of the line:

m=$\frac{△y}{△x}$

We know that the vertical distance is given by y=5 inches, and x=4 inches. Hence, the slope can be computed by substituting these quantities into the formula:

m=$\frac{5\: inches}{4\: inches}$=1.25

Using Point-Slope Equation

Sample Problem 4:

From the graph shown below, we have a line and a point K located at -2, 1. Its slope is given by m=-2. We are then asked to perform the following tasks:

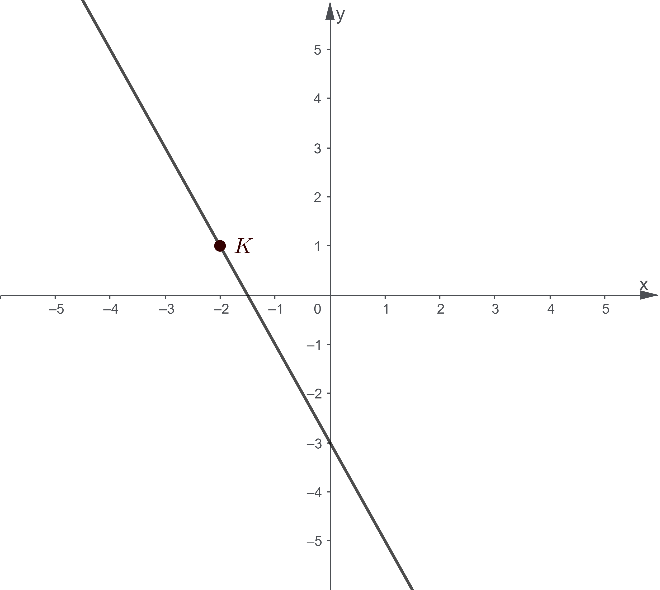
1. Write an equation representing the line by applying the Point-Slope Equation. Verify your answer by using a test point J(0,-3).

We recall that the Point-Slope Equation is given by:

y₂-y₁=m(x₂-x₁)

If we substitute the x and y coordinates of Point K into the equation, we get the following line equation:

y₂-1=(-2)(x₂-(-2))

Distributing -2 on both terms of the expression (x₂–2), we expand the product on the right-hand side of the equation:

y₂-1= -2x₂-4

Finally, by adding 1 to both sides of the equation, then dropping subscripts, we arrive at the line equation:

y₂=-2x₂-4+1

∴y=-2x-3

We can verify if the graph of the line equation passes through Point J by substituting the coordinates of this point into x and y, respectively:

-3=(-2×0)-3

Simplifying the expression on the right-hand side of the equation, we confirm that the equality holds:

-3=-3

2. Suppose another point L in the line lies at x=0. Without looking at the graph, where is this point located?

We are given the x-coordinate of point L. If we use the line equation we have previously derived for this problem, y=-2x-3, we can substitute the given x-coordinate to solve for the unknown y-coordinate of Point L:

y=(-2×0)-3

Simplifying the expression, we can solve for y:

y=0-3=-3

Therefore, we conclude that the Point L is located at (0,-3). We verify that this is the correct answer by looking at the given graph.

Using Slope-Intercept Equation

Sample Problem 5:

Without any graph given, we are given a line and a y-intercept located at b=-3. Its slope is also given by m=2. We are then asked to perform the following tasks:

1. Write an equation representing the line by applying the Slope-Intercept Equation.

We recall that the Slope-Intercept Equation is written as follows:

y=mx+b

If we substitute the given slope and intercept, we can directly write the line equation representing the given:

y=2x-3

2. Verify your answer by using a test point M(2,1).

We can verify if the graph of the line equation passes through Point M by substituting the coordinates of this point into x and y, respectively:

1=(2×2)-3

Simplifying the expression on the right-hand side of the equation, we confirm that the equality holds:

1=1

Sample Problem 6:

Suppose we have a point located at (-9, 4) and a y-intercept at b=1. We are then asked to perform the following tasks:

1. Solve for the slope of the line formed by these points.

We observe that this time, the slope is not given. What we have is the coordinates of one point in the line and the point at which the line intersects the y-axis.

To solve this problem, we substitute the given coordinates of the point to x and y, then we also substitute the value of b in the point-slope equation:

4=(m×-9)+1

Subtracting 1 from both sides of the equation gives us:

3=m×-9

Finally, by dividing -9 from both sides of the equation we can solve for the slope of the line:

m=-$\frac{1}{3}$

2. Verify your answer by substituting the given point into the Slope-Intercept Equation using the computed slope:

With m=-1/3 and b=1, the Slope-Intercept Equation representing the line is given by:

y=-$\frac{1}{3}$x+1

Substituting the coordinates of the point (-9, 4) into x and y, we get:

-4=-$\frac{9}{3}$+1

Simplifying the expression on the right-hand side of the equation, we confirm that the equality holds:

-4=-4

Summary

1. The slope of a line describes the relationship between the change in horizontal and vertical positions of a point as it goes through the line. It also tells us about the direction of a line depending on its value.
2. The Slope Formula is used to measure the slope using any two points in a line. It is given by: m=$\frac{y_2-y_1}{x_2-x_1}$
3. The tangent function can also determine the slope of a line, using the angle of inclination the line makes with the x-axis: m=tan⁡(θ)
4. The slope of a line can be positive (m>0), negative (m<0), zero (m=0), or undefined. These correspond to an increasing line, a decreasing line, a constant/horizontal line, and a vertical line, respectively.
5. The slope of two (or more) parallel lines are equal since they all have the same angle of inclination: m₁=m₂
6. On the other hand, the slope of two perpendicular lines are negative reciprocals of each other: m₃=-$\frac{1}{m_4}$
7. There are two types of line equations involving the slope:
8. The Point-Slope Equation describes a line using a given point and the slope of the line. It is written as: y₂-y₁=m(x₂-x₁)
9. The Slope-Intercept Equation describes a line using a given slope and the y-intercept of the line. It is given by: y=mx+b

Recommended Worksheets

Equation of a Straight Line (National Maritime Day Themed) Math Worksheets
Points and Lines (Stationery Themed) Worksheets
Graphing Lines in Slope-Intercept Form (Famous African-Americans Themed) Math Worksheets