What is an equality?
A relationship between two quantities or mathematical expressions that have the same value or represent distinct objects is called equality. To represent equality, we use the equal symbol or equal sign. Hence, we write two parallel horizontal symbols like “=” to show equality.

So, the equality between A and B is written as A = B which reads as A equals B or A is equal to B.
What is an inequality?
Inequality is a relationship between two numbers or algebraic expressions that are not equal. Inequalities can sometimes be presented as either question which can be solved or a statement of fact in the form of theorems. We can use four inequality terms to compare two quantities: not equal to, greater than, greater than or equal to, less than, and less than or equal to.
Not equal to
One of the symbols we use for inequality is not equal to sign. It is used to show that one value is not equal to the other. Hence, to show a not equal to relationship, we use two horizontal lines and a slash in the middle of it.

Therefore, if two quantities A and B are not equal, it is written as A ≠ B which reads as A is not equal to B.
Greater than
Greater than is also one of the inequalities used when a quantity is larger or bigger than the other quantity or quantities. Hence, to show that a number is greater than the other, we use two-equal length strokes that look like an acute angle going to the right.

So, to say that quantity A is greater than B, we denote it as A > B which reads as A is greater than B.
Greater than or equal to
Aside from greater than, we also use the term greater than or equal to show the relationship between two or more mathematical objects or inequalities. Greater than or equal assumes that the value of a variable can be equal to or greater than a certain number. The term “at least” means a value can be greater than or equal to. Hence, to show that a number is greater than the other, we use two-equal length strokes that looks like an acute angle going to the right and an underline under it.

Thus, to show that A is greater than B, we denote it as A ≥ B which reads as A is greater than or equal to B – which means A can be greater than B and can also be equal to B.
Less than
When the first value is smaller than the second value, we use the term less than. Less than is used to show the relationship between a smaller and larger value. To show inequality that a number is less than the other, we use the symbol two-equal length strokes that look like an acute angle going to the left.

Hence, to show that A is less than B, we denote it as A < B which reads as A is less than B.
Less than or equal to
Less than or equal to means that a variable is either less than or equal to the other number, expression, or term. Using the terms “at most”, “no more than”, “maximum of”, and “not exceeding” also means less than or equal to. Two-equal length strokes that look like an acute angle going to the left and an underline below it is the symbol used to show that one quantity is less than or equal to the other.

Therefore, to show that A is less than or greater than B, we denote it as A ≤ B which reads as A is less than or equal to B.
What are the equality and inequality symbols?
The table below summarizes all the symbols we use to show equality and inequality between two quantities.
| SYMBOL | TERM | EXAMPLE | HOW TO READ |
| = | equal | 1 + 1 = 4 | 1 plus 1 is equal to 21 plus 1 equals 2 |
| ≠ | not equal to | 2 + 1 ≠ 4 | 2 plus 1 is not equal to 4 |
| > | greater than | 9 > 5 | 9 is greater than 5 |
| < | less than | 3 < 10 | 3 is less than 10 |
Why do we use equality and inequality symbols?
The use of equality and inequality symbols can help us compare numbers, state the relationship between two or more mathematical objects that we are not yet certain of and use it for mathematical equations or inequality.
Compare numbers
One of the most important roles of using equality and inequality symbols is we get to compare two mathematical quantities. Let’s look at some of the examples below!
Using equal sign to compare mathematical objects
Example #1

In the given figure, we can see that on the left-hand side, we have two lollipops. On the right-hand side, we also have two lollipops. Since there is the same number of lollipops in the left and right-hand sign, we will use the equal sign to show equality between the two different groups of lollipops.
Using greater than or less than to compare mathematical objects
Example #1

By counting the number of cookies on both sides, we would know that the number of cookies on the left-hand side is greater than the number of cookies on the right-hand side. Hence, we use the greater than symbol to show the relationship between the cookies.
Example #2

In this second example, we can clearly see that there are more ice creams on the right-hand side than on the left-hand side. Thus, we use the less than sign to show that two is indeed less than three ice creams.
State relationships
When there are quantities that we are not certain of, we sometimes use equality and inequality symbols to know their relationships.
Example #1
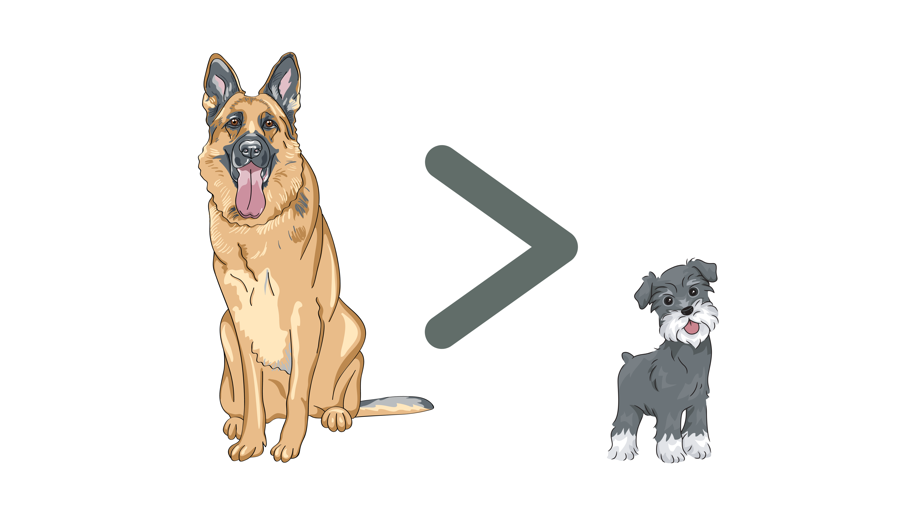
Explanation:
In the given figure, if we compare the relationship between the two dogs, we can clearly see that one is taller than the other. Hence, we can say that the dog on the right side is greater than the dog on the left side.
Example #2
\$1 = 100 cents
In this example, we know that in order for us to make a dollar out of cents is by having 100 cents. Hence, we can say
Example #2
Jace had 20 pens, but lost some in school. How many does he have now?
Since Jace lost some of his pens, then the number of pens that he has now must be less than 20. Hence, pens < 20.
Example #3
Angelina already spent \$50 and bought more clothes after. How much do you think did she spend?
It was already stated that Angelina had already spent \$50 before adding more clothes to buy. Hence, we can say that she spent money greater than \$50. Thus, Angelina’s expense > \$50.
Example #4
Danaya prepared 40 cupcakes for his visitors. The first group of twenty people ate about 24 cupcakes, and another group of people came. How many cupcakes were left?
While preparing, Danaya prepared exactly 40 cupcakes but then twenty people came and ate 24 cupcakes. Thus, we already know that cupcakes are now less than 40. But more people came so, we can say that cupcakes can also be equal to 40. Hence, we can translate the given statement to 0 ≤cupcakes < 40 which reads as cupcakes can be greater than or equal to 0 but less than 40 cupcakes.
How do we use the equality and inequality symbols?
We have listed all the possible reasons why we use equality and inequality symbols such as an equal sign, greater than, or less than sign. Now, how do we practice using these? Let’s look at some of the samples before.
Example #1
State the relationship that exists between the two numbers using equal, greater than, or less than sign.
| Examples | Explanation or Answer |
| 20 __ 20 | Since the left-hand side has the same value as the right-hand side. We will use the equal sign. Hence, we will have the statement 20 = 20 which reads as 20 is equals to 20. Thus, the answer is =. |
| 30 __ 45 | Since we know that 30 is less than 40, we will use the less than symbol to make the statement true. Hence, 30 < 40. Therefore, the symbol must be <. |
| 21 __ 8 | Since 21 is greater than 8, we will use the greater than symbol so the given statement will be true. Thus, 21 > 8. Therefore, the symbol that we need to use is >. |
| 8 __ 17 | Since the value on the left-hand side is smaller than the value of the number on the right-hand side, then we need to use the less-than symbol. So, to make the statement true, 8 < 17 which reads as 8 is less than 17. Therefore, the answer is <. |
Example #2
State the relationship that exists between the two numbers using equal, greater than, or less than sign.
| Examples | Explanation or Answer |
| 5 + 6 __ 5 + 3 | By adding the numbers on the left and right hand side, we will have the statement 5 + 6 = 11, and 5 + 3 = 9. Hence, we can rewrite the given as 11 __ 9. Thus,11 > 9 which reads as 11 is greater than 9. Therefore, the answer is >. |
| 2 + 4 __ 3 + 3 | By adding the numbers on the left and right hand side, we will have a new statement 2 + 4 = 6 and 3 + 3 = 6. So, rewriting it will give us 6 __ 6. Hence,6 = 6 which reads as 6 is equal to 6. Therefore, the answer is =. |
| 23 + 12 __ 35 + 4 | By adding the numbers on the left and right hand side, we will have a new statement 23 + 12 = 35 and 35 + 4 = 39. So, rewriting it will give us 35 __ 39. Hence,35 < 39 which reads as 35 is less than 39. Therefore, the answer is <. |
Example #3
State the relationship that exists between the two numbers using equal, greater than, or less than sign.
| Examples | Explanation or Answer |
| 20 – 13 __ 35 – 23 | The first step that we need to do is subtract the numbers on the left and right hand side, respectively. Hence, 20 – 13 = 7 and 35 – 23 = 12. Hence, we have a new statement 7 __ 12. Thus,7 < 12 which reads as 7 is less than 12. Therefore, to make the statement true, we need to add the symbol <. |
| 21 – 8 __ 39 – 26 | First thing that we need to do is to subtract the numbers on the left and right hand side of the mathematical statement. Thus, 21 – 8 = 13 and 39 – 26 = 13. Hence,13 = 13 which reads as 13 is equal to 13. Therefore, the use of = will make the statement true. |
| 100 – 54 __ 64 – 20 | By subtracting the numbers on the left and right hand of the mathematical statement, we will have 100 – 54 = 46 and 64 – 20. Giving us a new statement 46 __ 44. Hence, 46 > 44 which reads as 46 is greater than 44. Therefore, we need to use a greater than symbol, >, to make the statement true. |
Example #4
State the relationship that exists between the two numbers using equal, greater than, or less than sign.
| Examples | Explanation or Answer |
| 0 x 3 __ 1 x 3 | By multiplying the numbers on the left and right hand side, we will have a new mathematical statement. Hence, 0 x 3 = 0 while 1 x 3 = 1. Thus, by rewriting the new statement 0 __ 1 we can easily identify what symbol to use. So, 0 < 1 which reads as 0 is less than 1. Therefore, to make the statement true, we need to use the less than sign. |
| 6 x 4 __ 3 x 8 | By multiplying the numbers on the left and right hand sides, we will have a new mathematical statement. Hence, 6 x 4 = 24 while 3 x 8 = 24. Thus, by rewriting the new statement 24 __ 24, we can easily identify what symbol to use. So, 24 = 24 which reads as 24 is equal to 24. Therefore, to make the statement true, we need to use the equal sign. |
| 12 x 7 __ 7 x 13 | By multiplying the numbers on the left and right hand sides, we will have a new mathematical statement. Hence, 12 x 7 = 84 while 7 x 13 = 91. Thus, by rewriting the new statement 84 __ 91, we can easily identify what symbol to use. So, 84 < 91 which reads as 84 is less than 91. Therefore, a less than symbol will make the statement true. |
| 10 x 5 __ 6 x 8 | By multiplying the numbers on the left and right hand sides, we will have a new mathematical statement. Hence, 10 x 5 = 50 while 6 x 8 = 48. Thus, by rewriting the new statement 50 __ 48, we can easily identify what symbol to use. So, 50 > 48 which reads as 50 is greater than 48. Therefore, a greater than symbol will make the statement true. |
Example #5
State the relationship that exists between 10 meters and 10,000 centimeters.
Solution
| Step-by-Step Process | Explanation |
| 10 meters x 100 centimeters/1 meter | Convert 10 meters to centimeters. |
| 10 x 100 = 1000 centimeters | Simplify. |
| 1000 centimeters __ 10,000 centimeters | State the new mathematical statement. |
| 1000 centimeters < 10,000 centimeters | Since 1000 centimeters is smaller than 10,000 centimeters, then we need to use a less than symbol. |
| Therefore, 10 meters < 10,000 centimeters. |
Example #6
If Luna had \$150 and bought a bag that costs not more than \$100, how much money does she have left?
Solution
| Step-by-Step Process | Explanation |
| Luna’s money = \$150 | It is stated that Luna had \$150 before buying a bag. |
| cost of bag < \$100 | Because of the use of the word, “not more than \$100, we are certain that the cost of the bag is less than \$100. |
| ~\$100 __ \$150 | Since the cost of the bag is less than \$100, we need to write a mathematical statement that translates to ~\$100 __ \$150 which reads as about \$100 is __ to \$150. |
| ~\$100 < \$150 | To make the statement true, we know for a fact that \$100 is less than \$150. Hence, put < on the blank. |
| money left < \$150 | We can conclude that the money left on Luna is now less than \$150 after buying the bag. |
| Therefore, Luna’s money < \$150 after buying the bag. |
Recommended Worksheets
One-variable Inequalities (Time Themed) Worksheets
Understanding and Solving One-Variable Inequalities 6th Grade Math Worksheets
Comparing 3-Digit Numbers 2nd Grade Math Worksheets









