What is Ratio?
The ratio of two quantities of the same kind and in the same units is a fraction that shows how many times a quantity is of another quantity of the same kind. The ratio of two numbers “ a “ and “ b “ where b ≠ 0, is a ÷ b or $\frac{a}{b}$ and is denoted by a : b
In the ratio, a : b, the quantities or numbers a and b are called the terms of the ratio. The former “ a” is called the first term or antecedent and the latter term “ b” is called the second term or consequent.
Let us understand the ratio with the help of an example.
Suppose we have two brothers, Sam and Peter having their weights as 50 kg and d40 kg respectively. Now, if we compare the weight of Sam with the weight of Peter, we will get
$\frac{Weight\: of\: Sam}{Weight\: of\: Peter} = \frac{50}{4} = \frac{5}{4}$ = 5 : 4
Hence, we can say that the ratio of the weight of Sam to the weight of Peter is 5 : 4.
What is Proportion?
If the values of two quantities depend on each other in such a way that a change in one results in a corresponding change in the other, then the two quantities are said to be in proportion. For instance, let us consider the distance covered by a train in a given interval of time and speed. We can observe that if the speed is more, the train will travel more distance in a given period of time. Hence, we can say that the speed of a train and the distance covered by in a given period of time are in proportion. Let us take another example. Now, let us consider the speed of a moving train and the time taken by it to cover a certain distance. We can observe that the time taken by the train to travel a given distance will be less if the speed is more. In other words, as the speed increases the time taken to cover a given distance decreases. Therefore, we can say that the speed of a train and the time taken by it to cover a given distance are also in proportion.
In the above discussion, we can observe that two quantities may be linked together in such a way that both increase or decrease together. They can also be linked in a manner that if one of the quantities increases, the other quantity decreases and vice – versa. This means that we can have quantities in two different types of proportions – direct and inverse.
What is Direct Proportion?
If two quantities are linked with each other in such a way that an increase in one quantity leads to a corresponding increase in the other and vice – versa, then such a relation is called direct proportion. If two quantities are in direct proportion, we can also say that they are proportional to each other. Let us consider the number of articles bought by a person and the amount paid. It is clear that the larger the number of articles, the greater the amount paid will be. Therefore, the number of articles bought by a person and the amount paid is directly proportional to each other.
Also, if two quantities a and b are in direct proportion, then the ratio $\frac{a}{b}$ is always constant. This constant is called the constant of variation.
What is the Symbol for a direct proportion?
The symbol for direct proportion is “∝“ . Therefore, we can say that if two quantities a and b are in direct proportion, they can be written as –
a ∝ b
So, we have,
$\frac{a}{b}$ = k ( constant )
⇒ a = b k
What is Inverse Proportion?
If two quantities are linked with each other in such a way that an increase in one quantity leads to a corresponding decrease in the other and vice – versa, then such a relation is called inverse proportion. If two quantities are in inverse proportion, we can also say that they are inversely proportional to each other.
What is the Symbol for an inverse proportion?
The symbol for inverse proportion is the same as that of direct proportion, i.e. “∝“ . The difference lies in the positioning of a and b. Therefore, we can say that if two quantities a and b are in inverse proportion, they can be written as –
a ∝1b
So, we have,
a b= k ( constant )
Can Ratios be Equivalent?
We already know that a fraction does not change when its numerator and denominator are multiplied or divided by the same non-zero number. It is important to note here that in ratio as well, there is no change in the ratio if the first and the second term are multiplied or divided by the same non-zero number.
Let us understand this by an example.
Suppose we have the ratio 7 : 3. Now if we multiply both the first and the second term by 5, we will get the ratio 35 : 15. Similarly, if we multiply both the first and the second term by 3, we will get the ratio 21 : 9. So, we have
7 : 3 = 35 : 15 = 21 : 9
Hence, the ratios are equivalent in the same manner as fractions are.
Continued Proportion
Proportion is an equality of two ratios. For example, consider two ratios, 6 : 18 and 8 : 24. We can see that
6 : 18 = 1 : 3 and 8 : 24 = 1 : 3
Therefore, 6 : 18 = 8 : 24
Thus the ratios 6 : 18 and 8 : 24 are in proportion.
Therefore, we can say that four numbers a, b, c and d are said to be in proportion if the ratio of the first two is equal to the ratio of the last two. This means, four numbers a, b, c and d are said to be in proportion, if a : b = c : d
If four numbers a, b, c and d are said to be in proportion, then we write
a : b : : c : d, which is read as “ a is to b as c is to d” or “ a to b as c to d”. Here a, b, c and are the first second, third and fourth terms of the proportion. The first and the fourth terms of the proportion are called extreme terms or extremes. The second and the third terms are called the middle terms or means.
Let us understand this by an example.
Consider four terms 40, 70, 200 and 350. We find that 40 : 70 = 200 : 350. So, the given numbers are in proportion. Clearly, 40 and 350 are extreme terms and 70 and 200 are middle terms. We find that,
Product of extreme terms = 40 x 350 = 14000
Similarly, product of middle terms = 70 x 20 = 14000
Therefore,
Product of extreme terms = Product of middle terms
Thus, we can say that if four numbers are in proportion then the product of the extreme terms is equal to the product of the middle terms.
Three numbers a b c are said to be in continued proportion if a, b, b, c are in proportion.
Thus, if a, b and c are in proportion, then we have a : b : : b : c
Product of extreme terms = Product of middle terms
⇒ a x c = b x b
⇒ a c = b 2
⇒ b 2 = a c
Mean Proportion
If a, b and c are in continued proportion then b is called the mean proportional between a and c. This means that if b is the mean proportional between a and c then b 2 is equal to a c.
Using Ratios and Proportion in Real Life Situations
Let us now discuss about some real life examples, where two quantities are in proportion with each other.
Time and distance Graph
A common example of proportional relationships is that between time and distance when travelling at a constant speed. Let us plot a graph that shows the relationship between distance and time for a vehicle travelling at a constant speed of 30 miles per hour. Below we have some values defining the relation between time and distance when travelling at a constant speed of 30 miles per hour –
| Time | Distance |
| 0 | 0 |
| 1 | 30 |
| 2 | 60 |
| 3 | 90 |
| 4 | 120 |
On plotting the above values on a graph we will get –
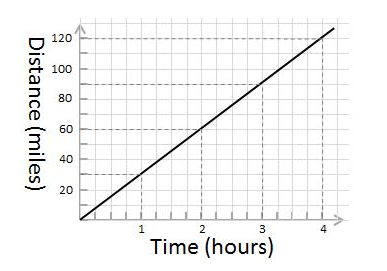
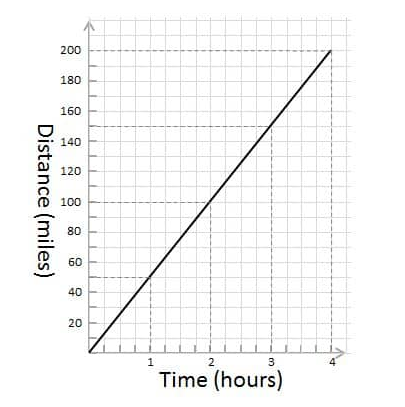
What if the constant speed of the vehicle would have been 50 miles per hour? The vehicle is travelling at a constant speed of 50 miles per hour. The slope of the graph is steeper. The steepness of the slope for directly proportional relationships increases as the value of the constant m (y = mx) increases.
Below we have some values defining the relation between time and distance when travelling at a constant speed of 50 miles per hour –
| Time | Distance |
| 0 | 0 |
| 1 | 50 |
| 2 | 100 |
| 3 | 150 |
| 4 | 200 |
On plotting the above values on a graph we will get –
Finding values of one quantity that is in a certain proportion with another quantity
Let us take an example.
Example
In a school library, the ratio of mathematics books to science books is the same as the ratio of science books to English books. If there are 450 books in Science and 300 books in English, find the number of books in mathematics.
Solution
We have been given that in a school library, the ratio of mathematics books to science books is the same as the ratio of science books to English books. Also, there are 450 books in Science and 300 books in English and we need to find the number of books in mathematics. Let us first summarise the information given to us.
Number of Science Books in the library = 450
Number of English Books in the library = 300
Also,
Ratio of mathematics books to science books = ratio of science books to English books
Now,
Ratio of science books to English books = 450 : 300
If we reduce this ratio to its simplest form, we will get,
450 : 300 = 3 : 2
Now, let the number of mathematics books in the library be p. therefore, we have,
Ratio of mathematics books to science books = ratio of science books to English books
⇒ p : 450 = 3 : 2
⇒ $\frac{p}{450} = \frac{3}{2}$
⇒ p = $\frac{3}{2}$ x 450
⇒ p = 675
Hence, the number of mathematics books in the library = 675.
Let us take another example
Example
The ratio of the length of a school ground to its width is 5 : 2. Find the length of the width of the ground is 50 m.
Solution
We have been given that the ratio of the length of a school ground to its width is 5 : 2. We need to find the length of the width of the ground is 50 m.
Let the length of the school ground be p metres.
Then, the ratio of the length to the width = p : 50
But, the ratio of the length to its width = 5 : 2
Therefore,
p : 50 = 5 : 2
⇒ $\frac{p}{50} = \frac{5}{2}$
⇒ p = $\frac{5}{2}$ x 50
⇒ p = 125
Hence, the length of the school playground = 125 m
Unitary Method
In order to understand the unitary method, let us consider the following example.
If the cost of 4 pens is £20, what will be the cost of 7 pens?
In order to find the solution of this problem, we can find the value of one unit. Thereafter we will find the value of the desired number of units by multiplying the value of one unit with the number of desired units. This method of problem solving is called as unitary method.
Therefore, we can say that
Value of one article = $\frac{Value\: of\: the\: given\: number\: of\: articles}{Number\: of\: articles}$
and,
Value of required number of articles = ( Value of one article ) x ( Required Number of articles)
Now, let us solve the above problem using unitary method.
We have,
Cost of 4 pens = £20
Therefore, Cost of 1 pen = £$\frac{20}{4}$ = £5
Now,
Cost of 7 pens = £5 x 7 = £35
Hence, cost of 7 pens = £35
Solved Examples
Example 1 The weight of 45 folding chairs is 18 kg. How many chairs can be loaded on a truck having a capacity of carrying 4000 kg of load?
Solution We have been given that the weight of 45 folding chairs is 18 kg. Here number of chairs is the unknown quantity and the weight is the known quantity. Therefore, we have,
Number of chairs in 18 kg weight = 45
So, number of chairs in 1 kg weight = $\frac{45}{18}$
Hence, the number of chairs in 1000 kg weight = $\frac{45}{18}$ x 1000 = 10000
So, we can say that 10000 chairs can be loaded on a truck having a capacity of carrying 4000 kg of load.
Example 2 Two numbers are in the ratio 3 : 4. If the sum of numbers is 63, find the numbers.
Solution We have been given that two numbers are in the ratio 3 : 4. Also the sum of numbers is 63. Let us first summarise the information given to us.
Sum of the terms of the ratio = 3 + 4 = 7
Sum of numbers = 63
Therefore, first number = 3/7 × 63 = 27
Second number = 4/7 × 63 = 36
Therefore, the two numbers are 27 and 36.
Key Facts and Summary
- The ratio of two quantities of the same kind and in the same units is a fraction that shows how many times a quantity is of another quantity of the same kind.
- The ratio of two numbers “ a “ and “ b “ where b ≠ 0, is a ÷ b or $\frac{a}{b}$ and is denoted by a : b
- In the ratio, a : b, the quantities or numbers a and b are called the terms of the ratio. The former “ a” is called the first term or antecedent and the latter term “ b” is called the second term or consequent.
- There is no change in the ratio if the first and the second term are multiplied or divided by the same non-zero number.
- A ratio a : b is said to be in its simplest form if its antecedent a and consequent b have no common factor other than 1.
- Proportion is an equality of two ratios.
- If four numbers are in proportion then the product of the extreme terms is equal to the product of the middle terms.
- Three numbers a b c are said to be in continued proportion if a, b, b, c are in proportion.
- If a, b and c are in continued proportion then b is called the mean proportional between a and c.
- Value of one article = $\frac{Value\: of\: the\: given\: number\: of\: articles}{Number\: of\: articles}$, and Value of required number of articles = ( Value of one article ) x ( Required Number of articles)
Recommended Worksheets
Ratio and Proportion (Armistice Day Themed) Math Worksheets
Solving Proportional Relationships Between Two Quantities 7th Grade Math Worksheets
Graphing Proportional Relationships and Identifying Slope of the Line 8th Grade Math Worksheets









