What is an order of operations?
When there are no special grouping symbols, math problems are usually solved from left to right. The order of operations rules tells you the order in which you should do the operations (addition or subtraction, multiplication or division) in a math expression. Math expressions are mathematical sentences (math sentences that do not have include an equal sign) or equations (math sentences that do have include an equal sign).
The order of operations is a set of principles in mathematics that represent rules or standards on which mathematical processes to perform first in order to evaluate a given mathematical expression.
The purpose of these rules is to remove notational ambiguity while allowing for the shortest feasible notation. Parentheses ( ), braces { }, and brackets [ ], can be used to indicate an alternate order of operations when it is desired to overrule or just emphasize the precedence conventions.
The following is the order of operations used in mathematics, science, technology, and many computer programming languages.
- exponents and root extractions
- multiplication or division
- addition or subtraction
This means that if a subexpression exists between two operators in a mathematical expression, the operator higher in the above list should be applied first.
PEMDAS
The acronym PEMDAS stands for Parenthesis, Exponents, Multiplication or Division, and Addition or Subtraction. This mnemonic is commonly used in the United States and France. More so, the phrase “Please Excuse My Dear Aunt Sally” is used to memorize the process of PEMDAS.

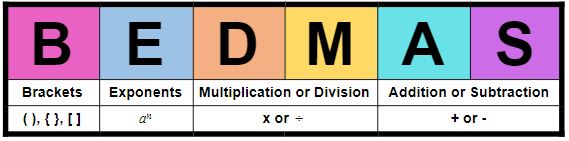
BEDMAS
Countries like Canada and New Zealand use the acronym BEDMAS to show the order of operations. BEDMAS means Brackets, Exponents, Multiplication or Division, and Addition or Subtraction.
BODMAS
In UK, Australia, India, Pakistan, and Bangladesh, they use the acronym BODMAS which means Brackets, Order, Division or Multiplication, and Addition and Subtraction. Order in this context means Exponentiation and Root extraction.

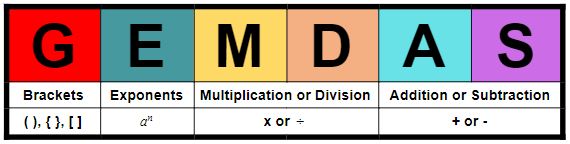
GEMDAS
GEMDAS is another acronym for the order of operation. GEMDAS means Groupings, Exponents, Multiplication or Division, and Addition or Subtraction.
Even though different countries have different acronyms for the order of operations, the order of operations remains the same.
How to determine order of operations?
The order of operations is used when there is more than one operation in a mathematical expression. When using PEMDAS, GEMDAS, BODMAS, or BEDMAS approaches, there is a set of rules that must be followed in order. Once you’ve mastered these rules, you’ll be able to perform numerous tasks at once. These rules are used to provide you with a structured approach in solving mathematical sentences.
How to apply the order of operations?
When performing PEMDAS or BODMAS, remember the following rules of the order of operations:
- Observe the given mathematical sentence.
- Parenthesis: Solve the expressions inside the grouping symbols. This can be done by solving the expressions inside first, then followed by the outside groupings. Usually, grouping symbols are patterned in this way – [ { ( ) } ]. This means we need to solve what is inside the parenthesis first, followed by the curly bracket, then by box brackets. Inside those grouping symbols, we also follow the same rule of order of operations.
- Exponents: Evaluate the result from step 2 with exponents.
- Multiplication or Division: Multiplying and dividing have the same priority. When you are reading from left to right, do whichever one you come to first. Skip adding and subtracting until after all multiplication and division have been done.
- Addition or Subtraction: Adding and subtracting have the same priority. When you are reading from left to right, do whichever one you come to first.
Example #1
What is the result of the mathematical sentence 10 + 20 x 4?
Solution
| Process | Step-by-Step Explanation |
| 10 + 20 x 4 | Observe the given expression. Since we need to do two different operations, we are going to apply the rules of the order of operation. |
| 10 + 20 x 4 | The order of operation (PEMDAS) tells us that, we need to do multiplication or division first. Hence, 20 x 4 = 80 |
| 10 + 80 = 90 | Add 10 and 80. |
| Therefore, 10 + 20 x 4 will result to 90. |
Example #2
Solve for 30 6 + 13 x 2 – 9.
Solution
| Process | Step-by-Step Explanation |
| 30 ÷ 6 + 13 x 2 – 9 | Observe the given expression. There are four different operations we need to do in the given example. Thus, we are going to apply the rules of the order of operation. |
| 30 ÷ 6 + 13 x 2 – 9 | The order of operation (PEMDAS) tells us that we need to do multiplication or division first. Hence, we will start by division. Thus, 30 ÷ 6 = 5 |
| 5 + 13 x 2 – 9 | Write the result of dividing 30 by 6. Then, do the multiplication process. Hence, 13 x 2 = 26 |
| 5 + 26 – 9 | Write the product of 13 and 2. Then, do the next process which is addition or subtraction. Since addition comes first, we are going to add 5 and 6. Thus, 5 + 26 = 31 |
| 31 – 9 = 22 | Subtract 9 from 31. |
| Therefore, 30 6 + 13 x 2 – 9 is equal to 22. |
Example #3
Find the result of the expression (2 x 3)2 + 7.
Solution
| Process | Step-by-Step Explanation |
| (2 x 3)2 + 7 | Observe the given expression. In the given expression, we have the grouping symbol of parenthesis and an exponent. Thus, it is convenient to use the order of operations. |
| (2 x 3)2 + 7 | The rules of PEMDAS say we need to solve first what is inside the grouping symbols. In this case, we have 2 x 3. Hence, 2 x 3 = 6 |
| (6)2 + 7 | Write the product of 2 and 3. Then, proceed to the next operation, which is the exponentiation. Thus,62 = 36. |
| 36 + 7 | Write the result of squaring 6. Then, do the last process which is addition. |
| 36 + 7 = 43 | Add 36 and 7. |
| Therefore, the result of the expression (2 x 3)2 + 7 is 43. |
Example #4
Solve for (4 + 3)2 x 23 ÷ 28.
Solution
| Process | Step-by-Step Explanation |
| (4 + 3)2 x 23 ÷ 28 | Observe the given expression. In the given expression, we have the grouping symbol of parenthesis and an exponent. Thus, we are going to use the rules of PEMDAS. |
| (4 + 3)2 x 23 ÷ 28 | Since we have the grouping symbol, we need to solve what is inside the parenthesis first. Hence,4 + 3 = 7 |
| (7)2 x 23 ÷ 28 | Write the sum of 4 and 3. Then, do the next process which is the exponentiation. Thus, 72 = 49 |
| 49 x 23 ÷ 28 | Write the result of squaring 7. Since we still have the exponent, we are going to work on that first. Thus, 23 = 8 |
| 49 x 8 ÷ 28 | Write the result of 23. Then, do the next operation which is multiplication or division. Since multiplication comes first, we are going to multiply 49 and 8. Thus,49 x 8 = 392 |
| 392 ÷ 28 = 14 | Write the product of 49 and 8. Lastly, divide it by 28. |
| Therefore, the result of the expression (4 + 3)2 x 23 ÷ 287 is 14. |
Example #5
What is the result of the expression [100 + {(62 + 4 x 10) 2} – 52] – 45 + 27?
Solution
| Process | Step-by-Step Explanation |
| [100 + {(62 + 4 x 10) ÷ 2} – 52] – 45 + 27 | Observe the given expression. The example may be a long expression, but the rules of the order of operation will help us find the result quickly. |
| [100 + {(62 + 4 x 10) ÷ 2} – 52] – 45 + 27 | Let’s start by solving the terms inside the parenthesis. Hence, we will first focus on (62 + 4 x 10) and apply PEMDAS rules. Thus, we will start by squaring 6. 62 = 36 |
| [100 + {(36 + 4 x 10) ÷ 2} – 52] – 45 + 27 | Write the result of squaring 6. Then, work on the next process inside (62 + 4 x 10) which is multiplication. Thus, 4 x 10 = 40 |
| [100 + {(36 + 40) ÷ 2} – 52] – 45 + 27 | Write the product of 4 and 10. Then, proceed with the addition. Hence, 36 + 40 = 76 |
| [100 + {76 ÷ 2} – 52] – 45 + 27 | Write the sum of 36 and 40, and remove the parenthesis. Now, to remove the braces, we need to find the quotient of 76 and 2. Thus,76 2 = 38 |
| [100 + 38 – 52] – 45 + 27 | Remove the braces and write the quotient of 76 and 2. Now, we are left with the grouping [100 + 38 – 52]. Since we have an exponent, get the square of 5. Thus, 52 = 25 |
| [100 + 38 – 25] – 45 + 27 | Write the square of 5. Then, let’s proceed with the addition or subtraction. Since the addition comes first, we will work on that. Thus, 100 + 38 = 138 |
| [138 – 25] – 45 + 27 | Write 138, then get the difference of 138 and 25. Thus,138 – 25 = 113 |
| 113 – 45 + 27 | Write 113 and remove the brackets. Now, we need to subtract 45 from 113. Hence, 113 – 45 = 68 |
| 68 + 27 = 95 | Write the difference and add 27. Thus,68 + 27 = 95 |
| Therefore, the result of the expression [100 + {(62 + 4 x 10) ÷ 2} – 52] – 45 + 27 is 95. |
Children are often overwhelmed by a complicated math expression or equation. Remind them to focus on just one step at a time. Big tasks become easier to think about and accomplish when broken down into small steps.
What is the difference of using the order of operations?
We already know that the rules we use in the order of operations help us solve long mathematical expressions, but do they really make a difference compared to simply doing the left to right process? Let’s see using some of the examples below.
Example #1
Simplify the expression 3 + 4 x 5.
Solution

Now, let’s try another example of having grouping symbols.
Example #2
What is the result of 3 + 4 x 5? How about (3 + 4) x 5?
Solution
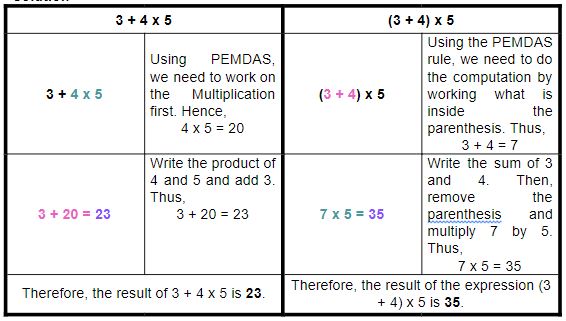
See how the use of grouping symbols can result in a different answer. Now, let’s try comparing another example.
Example #3
Compare the result of the expressions (2 + 3)2 + 7 and 22 + 32 + 7.
Solution

What is the importance of the order of operations?
The order of operations is significant because it ensures that everyone can read and solve a problem in the same manner. Formulas for real-world calculations in finance and science would be meaningless without a consistent order of operations, and it would be difficult to determine if you were obtaining the right answer.
The order of operations keep mathematics consistent. We have seen examples of how the rules in the order of operations may come up with different answers even though we use the same numbers. It establishes a standard for solving equations; otherwise, complex problems may have multiple solutions.
In a nutshell, rules are there to be followed. If these norms about order of operations did not exist, each solver would solve an algebraic in a unique method, making it less likely to arrive at a right answer.
Recommended Worksheets
Basic Order of Operations (MDAS) (Soccer Themed) Worksheets
Order of Operations (PEMDAS) (Work from Home Themed) Worksheets
Order of Operations and Grouping Symbols 5th Grade Math Worksheet









