Home » Math Theory » Algebra » Inverse Functions

Inverse Functions

Introduction

The concept of function is of paramount importance in mathematics and among other disciplines as well. An inverse function is a function that undoes the action of another function. Let us recapitulate what we know about functions that are relevant to the understanding of inverse functions.

Function as a set of ordered pairs

Let A and B be two non-empty sets. A relation from A to B i..e a subset of A x B is called a function or a mapping or a map from A to B if,

  1. For each a ∈ b, there exists b ∈ B such that ( a, b ) ∈ f
  2. ( a, b ) ∈ f and ( a, c ) ∈ f ⇒ b = c

Thus a non-void subset of A x B is a function from A to B if each element of A appears in some ordered pair in f and no two pairs in f have the same first element.

Domain, Co-domain and Range of a Function

Let f : A → B. then the set A is known as the domain of f and the set B is known as the range co-domain of f. the set of all f-images of elements of A is known as the range of f or image set of A under f and is denoted by f ( A ).

Thus f ( A ) = { f (x)  : x ∈ A } = Range of f

Onto Functions

A function A → B is said to be onto function or a surjection if every element of B is the f-image of some element of A, i.e. f ( A) = B or range of f is the c-domain of f.

Thus f : A → B is an onto function iff for each b ∈ B there exists a ∈ A such that f ( a ) = b

One-One Functions

A function A → B is said to be a one-one function or an injection if different elements of A have different images of B.

Thus f : A → B is one-one

⇔ a ≠ b ⇒ f ( a ) ≠  f ( b ) for all a, b ∈ A

 ⇔ f ( a )  = f ( b ) ⇒ a = b for all a, b ∈ A

Many-One Functions

A function A → B is said to be a many-one function if two or more elements of set A have the same image in B.

Thus f : A → B is many-one if there exists x, y ∈ A such that x≠ y but f ( x ) = f ( y )

Now let us understand what we mean by inverse functions.

What is an Inverse Function?

Let A and B be two sets and let f :  A → B be a function. If we follow a rule in which elements of B are associated to their pre-images, then we will find that under such a rule there may be some elements in B which are not associated to elements in A. this happens when f is not an onto map. Therefore all elements in B will be associated to elements in A if f is an onto map. Also, if it is a many-one function then under the said rule an element in B may be associated to more than one element in A. Therefore, an element in B will be associated to a unique element in A if f is an injective map.

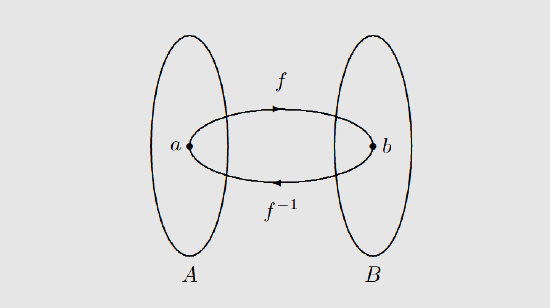
We can infer from the above discussion that if f : A → B is a bijection, we can define a new function from B to A which associates each element y ∈ B to its pre-image f –1 ( y ) ∈ A. Such a function is known as the inverse of function f and is denoted by f -1 . Therefore we can now define an inverse function as:

Let f : A → B be a bijection. Then a function g : B → A which associates each element y ∈ B to a unique element x ∈ A such that f ( x )  = y is called the inverse of f. This means,

f ( x ) = y ⇔ g ( y )  = x

Therefore, if f : A → B is a bijection function, then f-1 : B → A such that f ( x ) = y ⇔ f -1 ( y )  = x

Functions that have inverse are called one-to-one functions.

Algorithm to Find the Inverse of a Function

Now that we have understood what we mean by an inverse function it is important to learn how to actually find the inverse of a given function. The following algorithm defines the steps that are to be followed in order to find the inverse of a given function –

Put f ( x)  = y where y ̬∈ B and x ∈ A

Now, solve f ( x ) = y to obtain x in terms of y.

In the relation obtained in the above step, replace x by f -1 ( y ) to obtain the required inverse of f.

Let us understand this through an example.

Example              

Find the inverse for the function f ( x ) = 3x−4. State the domain and range of the inverse function. Verify that f−1( f ( x ) ) = x

Solution              

We will find the inverse of the function through the following steps –

First, we have been given that f ( x ) = 3x – 4.

Therefore, if  y = 3x – 4, this means that 3x = 4 + y which further implies that –

$x=\frac{1}{3}y+\frac{4}{3}$

Now, we will rewrite the above equation as:

$$ and let y be equal to f-1 ( x )

Hence, we will have,

f-1 ( x ) =$y=\frac{1}{3}x+\frac{4}{3}$

No, since the domain of f is (−∞,∞) and the range of f−1 is (−∞,∞) and since the range of f is (−∞,∞) and the domain of f−1 is (−∞,∞).

Therefore,

Domain of f−1 is (−∞,∞).

Range of f−1 is (−∞,∞)

Now, let us move to the second part of the question.

We are required to verify that f−1(f(x) = x

In order to verify this, we will write the function as

f−1 (f(x)) = f−1 (3x−4) = $\frac{1}{3}(3x-4)+\frac{4}{3}$

$=x-\frac{4}{3}+\frac{4}{3}=y$

Hence f−1( f ( x ) ) = x

It is important to note here that for f -1(f(x)) to be the inverse of f ( x) both  f –1(f(x)) = x and f ( f-1 (x)) = x for all x in the domain of the inside function.

Example              

Let f : N → R be a function defined as f ( x ) = 4x2 + 12x  + 15. Show that f : N → Range ( f ) is invertible. Find the inverse of f.

Solution              

We have been given that f : N → R be a function defined as f ( x ) = 4x2 + 12x  + 15. We are required to prove that f : N → Range ( f ) is invertible and then find the inverse of f.

In order to prove that f is invertible, is tis sufficient for us to show that f : N → Range ( f ) is a bijection.

f is one-one. For any x, y ∈ N, we find that,

f ( x ) = f ( y )

⇒ 4x2 + 12x  + 15 = 4y2 + 12y + 15

⇒ 4 (x2 – y2 ) + 12 ( x – y ) = 0

⇒ ( x – y ) ( 4x  + 4y + 3 ) = 0

⇒ x – y = 0

 ⇒ x = y

Therefore, f : N → Range ( f ) is one-one.

Obviously, f : N → Range ( f ) is onto. Hence, f : N → Range ( f ) is invertible.

Now, let us find the inverse of the function.

Let f-1 denote the inverse of f, then

fof -1 ( x ) = x for all x ∈ Range ( f )

⇒ f ( f -1 ( x )) = x for all  x ∈ Range ( f )

⇒ 4 f -1 ( x )2 + 12 f -1 ( x ) + 15 = 0 for all x ∈ Range ( f )

4 { f -1 ( x )2 + 12 f -1 ( x ) + 15 – x  = 0

Solving this equation for f-1 ( x ), we get

f-1 ( x ) = $\frac{-12\pm \sqrt{(144-16 (15-x ))}}{8}$

⇒ f-1 ( x ) = $\frac{-12\pm \sqrt{(16x-96)}}{8}=\frac{-3\pm \sqrt{(x-6)}}{2}$

⇒ f-1 ( x ) = $\frac{-3\pm \sqrt{(x-6)}}{2}$

Hence, the inverse of f = $\frac{-3\pm \sqrt{(x-6)}}{2}$

Properties of an Inverse Function

The following are the properties of an inverse function.

  1. The inverse function of a bijection is unique.
  2. The inverse of a bijection is also a bijection.
  3. If f : A → B is a bijection and g : B → A is the inverse of f then fog = IB and gof = IA, where IA and IB are the identity functions on the sets A and B respectively.
  4. If f : A → B and g : B → C are two bijections, then gof : A → C is a  bijection and (gof)-1 = f-1og-1
  5. Let f : A → B and g : B → C be two functions such that gof = IA, and fog = IB. then f and g are bijections and g = f-1.
  6. Let f : A → B be an invertible function. Then the inverse of f-1 is f.

Relation between Graphs of a function and Its Inverse

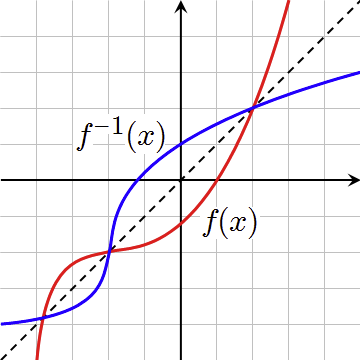
The graph of a bijection f and its inverse f-1 are closely related.  If ( a, b ) is a point on the graph of f, then b = f ( a ) and a =  f -1 ( b ). As b is the domain of f-1, therefore, ( b, f – 1 ( b ) ) is the point on the graph of f-1. But ( b, f – 1 ( b ) ) = ( b, a ). Therefore, ( b, a ) is on the graph of f-1.

Thus if ( a, b ) is a point on the graph of f, then ( b, a ) is a point on the graph of f-1. But, ( a, b ) and (b, a  ) are reflections of one another in the line y =  x. Thus the graph of f-1 may be obtained by reflecting the graph of f in the line mirror y = x.  this means that graphs of f and f-1 are mirror images of each other in the line mirror y =  x.

From the above discussion, we can also infer that if the graphs of f ( x ) and f -1( x ) intersect each other, their points of intersection lie on the line y = x. consequently, solutions of the equation f ( x ) = f -1 (x) are same as that of f ( x ) = x or f-1 ( x ) = x.

Do we have an inverse function of every function? Let us find out.

Determining the inverse of a function

It is important to note about the inverse function is that the inverse of a function is not the same as its reciprocal, i.e., f – 1 (x) ≠ 1/ f(x). Therefore, not all functions have an inverse, and hence it is important to check whether a function has an inverse before embarking on determining its inverse. So how do we check whether an inverse function exists for a function or not? The following rule applies in this case –

A function f has an inverse if and only if when its graph is reflected about the line y = x, the result is the graph of a function. The following test is used to determine whether the function has an inverse or not.

Horizontal Line Test

The following steps are followed in the horizontal line test to determine whether there exists the inverse of a function.

  1. Let f be a function.
  2. If any horizontal line intersects the graph of f more than once, then f does not have an inverse.
  3. If no horizontal line intersects the graph of f more than once, then f does have an inverse.

Let us understand this by an example

Example             

Graph the function, f(x) =  (x – 3 ) x2 and determine whether or not it has an inverse.

Solution              

The graph of the given function will be

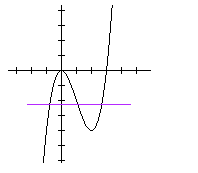
We can see that there is a horizontal line that hits the graph more than once.

This means that the function f is not one-to-one.

Hence, we can say that the function f does not have an inverse.

Remember

  1. A non-void subset of A x B is a function from A to B if each element of A appears in some ordered pair in f and no two pairs in f have the same first element.
  2. Let f : A → B. then the set A is known as the domain of f and the set B is known as the range co-domain of f.
  3. Let f : A → B be a bijection. Then a function g : B → A which associates each element y ∈ B to a unique element x ∈ A such that f ( x )  = y is called the inverse of f.
  4. A function A → B is said to be onto function or a surjection if every element of B is the f-image of some element of A, i.e. f ( A) = B or range of f is the c-domain of f.
  5. A function A → B is said to be a one-one function or an injection if different elements of A have different images of B.
  6. A function A → B is said to be a many-one function if two or more elements of set A have the same image in B.
  7. The inverse function of a bijection is unique.
  8. The inverse of a bijection is also a bijection.
  9. If f : A → B is a bijection and g : B → A is the inverse of f then fog = IB and gof = IA, where IA and IB are the identity functions on the sets A and B respectively.
  10. If f : A → B and g : B → C are two bijections, then gof : A → C is a  bijection and (gof)-1 = f-1og-1
  11. Let f : A → B and g : B → C be two functions such that gof = IA, and fog = IB. then f and g are bijections and g = f-1.
  12. Let f : A → B be an invertible function. Then the inverse of f-1 is f.
  13. The graph of f-1 may be obtained by reflecting the graph of f in the line mirror y = x. 
  14. A function f has an inverse if and only if when its graph is reflected about the line y = x, the result is the graph of a function. 

Multiplication of Functions (Travel and Tours Themed) Worksheets
Division of Functions (Health and Fitness Themed) Worksheets
Subtraction of Functions (Tropical Themed) Worksheets

Browse All Worksheets

Link/Reference Us

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!

  • "Inverse Functions". Helping with Math. Accessed on April 25, 2024. https://helpingwithmath.com/inverse-functions/.

  • "Inverse Functions". Helping with Math, https://helpingwithmath.com/inverse-functions/. Accessed 25 April, 2024.

  • Inverse Functions. Helping with Math. Retrieved from https://helpingwithmath.com/inverse-functions/.