Comparing and Ordering Integers

What are integers?

An integer is a number that can be written without a fractional component. In other words, an integer is a whole number that can be positive, negative, or zero. Hence, we can say that integers are the collection of whole numbers and negative numbers. The set of integers is represented by Z and can be written as – 

Z = { …….. – 3, – 2 , – 1 , 0 , 1 , 2 , 3 …….. }

Why Are Big Negative Numbers Less Than Small Ones?

We are used to big positive numbers meaning a big value – the bigger the number, the more, or higher, or longer, or expensive, or whatever the number represents.

With negative numbers, we have to remember that as the digit gets bigger, the number gets smaller. Think what the number represents. Think what the value is.

• The amount of money you have gets lower the more you owe.
• The temperature gets lower, the colder it gets
• The more you take away, the less you have

How are integers represented on a number line?

Recall that a number line is a straight horizontal line with numbers placed at even intervals that provides a visual representation of numbers. Primary operations such as addition, subtraction, multiplication, and division can all be performed on a number line. The numbers increase as we move towards the right side of a number line while they decrease as we move left. 

Parts of a Number Line

A number line consists of a ray on which the numbers are plotted in an increasing order from left to right. A number line can be divided into three parts – 

1. Negative Numbers – The negative numbers are plotted to the left of the point 0 or the origin.
2. Origin – The number zero ( 0 ) is considered as the origin of the number line and is usually plotted at its centre.
3. Positive Numbers – The positive numbers are plotted to the right of the point 0 or the origin.

Integers are therefore represented on a number line as shown below – 

Above is a visual representation of a standard number line for representing integers. As is clearly visible, as we move from left to right, there is an increase in the value of integers while it decreases when we move from right to left.

Vertical representation of a number line

For the convenience of understanding the ordering of integers, we can represent a number line in a vertical manner as well.  This allows a better understanding of whether an integer is greater or small than another integers.

Looking at numbers on a vertical number line can be useful.

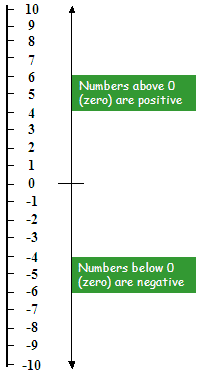
Zero is neither positive or negative

We can see above as the numbers get bigger as we move above on the number line. 

Using number line for comparing integers?

We now know how to plot integers on a number line. Can we use a number line for comparing integers? Suppose we have two numbers  – 5 and  – 3 and we wish to find out which is the greater of the two numbers. Let us find this using a number line.

For comparing these two numbers, we shall first plot both the numbers on a number line. We will have,

We can see above that the yellow circle represents the number -5 while the red circle represents the number -3. Now we have learnt that as we move from left to right, there is an increase in the value of integers. Since, – 3 is to the right of the number –  5 on the number line, this means that  – 3 > – 5 or we can say that  – 5 < – 3. In this way, we can use the number line to compare different integer values. 

Using number line for comparing integers 

A number line helps you visualize which a greater number among two or more numbers is. The farther a number is on the right, the greater it is.

Let us consider an example.

Example

Let us consider the following numbers for comparison – 

-2, 8 and 3

Solution

In order to compare these numbers, first, we will plot these numbers on the number line. We will have, 

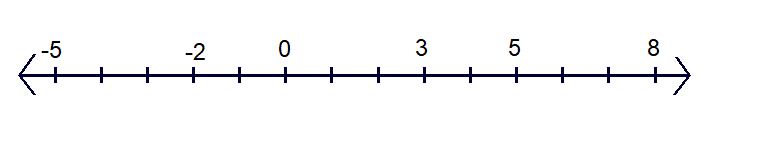
Out of the three given numbers, -2 is on the farthest left while 8 is on the farthest right placing 3 between these numbers. Hence the increasing orders of the numbers -2, 8 and 3 will be  -2 < 3 < 8 or 8 > 3 > – 2.

Ordering of Integers

The ordering of integers is based on the positive and negative aspects of integers. We know that the integers are that greater than 0 are called positive integers and the integers that are less than 0 are called negative integers. This ordering of integers can be in two ways – 

1. Ascending order
2. Descending order

Let us understand both of them one by one.

Ascending order of integers

When we say that the integers are placed in ascending order, we mean that the integers are placed from the lowest to the highest value. For instance, if we have the numbers, 3, 1 and 6, what will be the ascending order in which these integers can be placed? We know that out of these three numbers, 3, 1 and 6, the smallest number is 1. After 1, the next number on the number line will be 3. Lastly, after 3 the next number on the number line will be 6. In this manner, we can list these numbers as 1, 3 and 6. This is the ascending order of these three integers, which means that they have been placed from the smallest to the largest number in value.

Let us understand this by an example.

Example

Arrange the following numbers in ascending order – 

6 , – 5 , 4 , – 1 , 9

Solution

We have been given the numbers and we need to arrange them in ascending order.  We know that in order to arrange these numbers in ascending order, we need to place them from the smallest to the largest numbers in value. From the numbers given to us, let us first check which negative numbers have been given. The negative numbers are – 5  and  – 1. Let us first compare these two numbers.  The following is the arrangement of these numbers on the number line.

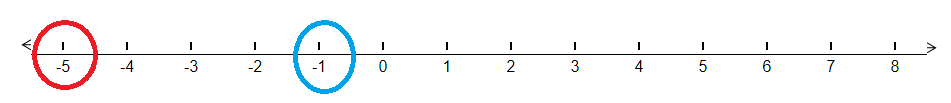
We can see that – 1 is on the right side of – 5 on the number line. This means that – 1 > – 5.

The other remaining positive numbers are also greater than these two negative numbers. Therefore, we can say that the smallest number of the given numbers is  – 5. Also, since the only negative number given in the question is – 1, therefore, the next number in order will be  – 1.

Hence, on comparing the negative numbers we have,  – 5 <  – 1 . . . . .  . . . . . . . . . . . . . . .   ( 1 )

Now, let us compare the positive numbers. For doing so, let us plot the numbers on the number line. We will have,

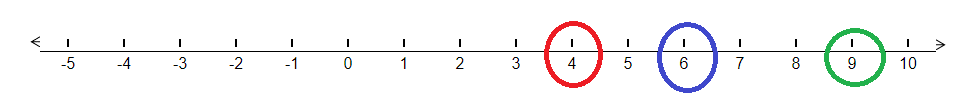
From above, we can see that out of the given numbers, 4 lies on the left most side. This means that 4 is the smallest of the given positive integers. Also, we know that all positive integers are greater than negative integers. Therefore we can say that 4  is less than the remaining positive integers but is greater than the given negative integers. So the ascending order gets now updated as  – 

-5 < – 1 < 4 . . . . .  . . . . .  . . .  . . . . . . . . . . . (  2 )

Now, let us consider the next number highest on the number line. We have the number 6. So, 6 > 4 . Hence, the ascending order gets now updated as  – 

-5 < – 1 < 4 < 6  . . . . .  . . . . .  . . .  . . . . . . . . . . . (  3 )

Lastly we have the number 9 which is on the right most side of the number line. This means that 9 > 6. The ascending order gets now updated as  – 

-5 < – 1 < 4 < 6 < 9 . . . . .  . . . . .  . . .  . . . . . . . . . . . (  4 )

Hence, the ascending order of the given numbers will be – 5 < – 1 < 4 < 6 < 9

Descending order of integers

When we say that the integers are placed in descending order, we mean that the integers are placed from the highest to the lowest value. For instance, if we have the numbers, – 3, – 1 and – 6, what will be the descending order in which these integers can be placed? We know that out of these three numbers, – 3, – 1 and – 6, the largest number is – 1. After, – 1, the next number towards the left side on the number line will be – 3. Lastly, after – 3 the next number towards the left on the number line will be – 6. In this manner, we can list these numbers as – 1, – 3 and – 6. This is the descending order of these three integers, which means that they have been placed from the largest to the smallest number in value.

Let us understand this by an example.

Example

Arrange the following numbers in ascending order – 

-6 ,  5 , – 4 ,  1 , – 9

Solution

We have been given the numbers and we need to arrange them in descending order.  We know that in order to arrange these numbers in descending order, we need to place them from the largest to the smallest numbers in value. From the numbers given to us, let us first check which positive numbers have been given. The negative numbers are 5 and  1. Let us first compare these two numbers.  The following is the arrangement of these numbers on the number line.

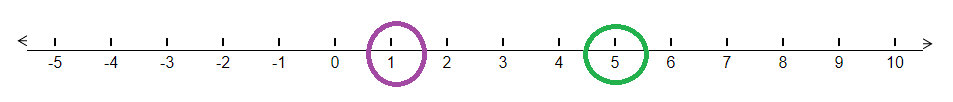
We can see that 1 is on the left side of 5 on the number line. This means that 1 < 5.

The other remaining negative numbers are also lesser than these two positive integers. Therefore, we can say that the largest number of the given numbers is  5. Also, since the only other positive number given in the question is 1, therefore, the next number in order will be 1.

Hence, on comparing the positive integers we have, 5 > 1 . . . . . . . . .  . . . . . . . . . . . . . . .   ( 1 )

Now, let us compare the negative integers. For doing so, let us plot the numbers on the number line. We will have,

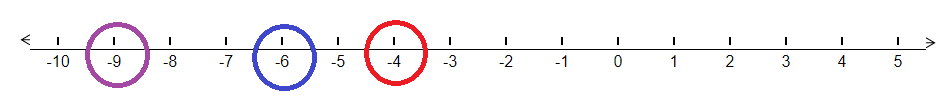
From above, we can see that out of the given numbers, – 4 lies on the right most side. This means that – 4 is the largest of the given negative integers. Also, we know that all positive integers are greater than negative integers. Therefore we can say that – 4  is greater than the remaining negative integers but is lesser than the given positive integers. So the descending order gets now updated as  – 

5 > 1 > – 4 . . . . . . . . . . . . . . . . .  . . . . .  . . . . .  . . .  . . . . . . . . . . . . .  . . . . . . . . . . (  2 )

Now, let us consider the next negative integer to the left of – 4 on the number line. We have the number – 6. So, – 6 < – 4 . Hence, the descending order gets now updated as  – 

5 > 1 > – 4 > – 6 . . . . . . . . . . . . . . . . . . . .  . . . . .  . . .  . . . . . . . . . . . . . . . . . . . . . . . . . . (  3 )

Lastly we have the number – 9 which is on the left most side of the number line. This means that – 9 < – 6. The descending order gets now updated as  – 

5 > 1 > – 4 > – 6 > – 9 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .  . . . . .  . . .  . . . . . . . . . . . (  4 )

Hence, the descending order of the given numbers will be 5 > 1 > – 4 > – 6 > – 9

Solved Examples

Example 1 Which is greater, -5 or -3?

Solution Locate both numbers on the number line. Numbers to the right are greater. -3 is to the right of -5 so -3 is greater.

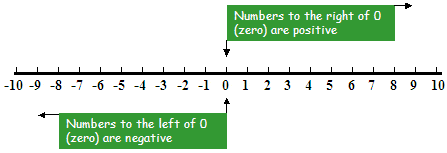
Example 2 Put the following numbers in order starting with the least. -23, 17, -32, 2, -4, 0

Solution Start looking at the negative numbers as these are always less than positive numbers. Start with the “biggest” negative number ( -32) as that has the lowest value.

Find the next “biggest” negative number (-23) and continue until the negative numbers are in order.

Zero and positive numbers can then be put into order to give the following complete list:

-32 , -23 , -4 , 0 , 2 , 17

Example 3 Which of these numbers is greater than -6 but less than 4?
-8, -10, 5, -4, 0

Solution Start by finding all the numbers that are less than -6. This gets rid of -8 and -10 (to the left of -6 on the number line). Next, we will get rid of any number that is greater (not less) than 4. 

This means 5 is out leaving:

-4 and 0

Key Facts and Summary

1. An integer is a whole number that can be positive, negative, or zero.
2. The numbers, 1, 2, 3, 4 ….. are natural numbers and are called positive integers while the numbers – 1, – 2 , – 3 etc. ate called negative integers. 
3. An integer is a number that can be written without a fractional component.
4. A number line is a straight horizontal line with numbers placed at even intervals that provides a visual representation of numbers.
5. The negative numbers are plotted to the left of the point 0 or the origin.
6. The number zero ( 0 ) is considered as the origin of the number line and is usually plotted at its centre.
7. The positive numbers are plotted to the right of the point 0 or the origin.
8. A number line helps you visualize which a greater number among two or more numbers is.
9. The ordering of integers is based on the positive and negative aspects of integers.
10. When we say that the integers are placed in ascending order, we mean that the integers are placed from the lowest to the highest value.
11. When we say that the integers are placed in descending order, we mean that the integers are placed from the highest to the lowest value.

Recommended Worksheets

Multiplication of Integers with Like Signs (Math Awareness Month Themed) Worksheets
Multiplication of Integers with Unlike Signs (Banking and Finance Themed) Worksheets
Division of Integers with Unlike Signs (Basketball Themed) Worksheets