Introduction
A fundamental group of mathematical formulas is algebraic identities. They assist you in carrying out calculations in quick, uncomplicated steps and are the building blocks of algebra. Many mathematical operations must be performed to solve certain algebraic problems.
For all possible values of the variables, an algebraic identity is a relationship in which the left side of the equation is precisely equivalent to the right side.
In this article, we’ll aim to become familiar with all the algebraic identities, their proofs, and how to apply them to mathematical calculations.
Algebraic Identities
Definition
Algebraic identities are equations in which the right-hand side of the equation’s value is exactly equal to the left-hand side of the equation’s value. Any value for the variables satisfies them.
Identity vs. Conditional
Number relationships can be expressed using identity and conditional equations. The term “identity equation” refers to an equation that holds true for every value of the variable.
A conditional equation is one that is false for at least one value.
The table below shows some examples of the identity and conditional equations.
| Examples of Conditional Equations | Examples of Identity Equations |
| 3x = 12 This equation is false when the value of x is not equal to 4. 10x – 3 = 17 This equation is true when x is equal to 2. | ( x + 1 )2 = x2 + 2x + 1 x2 – 6x + 9 = ( x – 3 )2 Both equations are satisfied for any value of x. |
List of Algebraic Identities
Algebraic identity states that the left and right sides of the equation are equal for all values of the variables. To determine the values of unknown variables, algebraic identities are used. These algebraic identities are some of the most common ones:
| ( a + b )2 = a2 + 2ab + b2 |
| ( a – b )2 = a2 – 2ab + b2 |
| ( a + b ) ( a – b ) = a2 – b2 |
| ( a + b )3 = a3 + 3a2 b + 3ab2 + b3 |
| ( a – b )3 = a3 – 3a2 b + 3ab2 – b3 |
Algebraic Identities Proof
We will be able to visualize each of the identities and understand them more fully with the help of the algebra identities proofs that are provided below.
Proof: ( a + b )2 = a2 + 2ab + b2
LHS = ( a + b )2 Starting with the left-hand side of the equation
LHS = ( a + b ) ( a + b )
LHS = a2 + ab + ab + b2 Multiplying each term
LHS = a2 + 2ab + b2
LHS = RHS
Visual Proof of ( a + b )2 = a2 + 2ab + b2
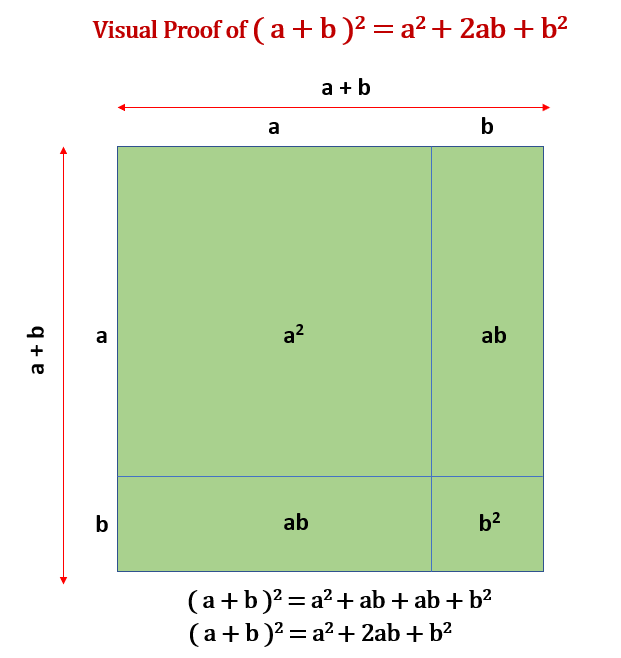
Proof: ( a – b )2 = a2 – 2ab + b2
LHS = ( a – b )2 Starting with the left-hand side of the equation
LHS = ( a – b ) ( a – b )
LHS = a2 – ab – ab + b2 Multiplying each term
LHS = a2 – 2ab + b2
LHS = RHS
Visual Proof of ( a – b )2 = a2 – 2ab + b2
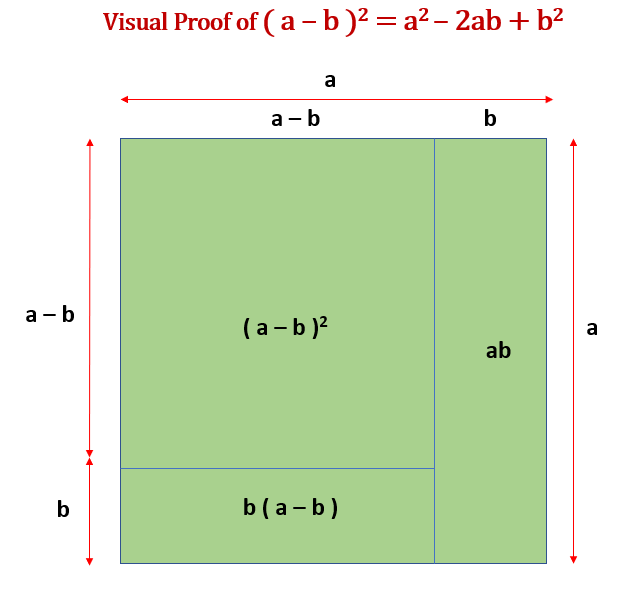
Proof: ( a + b ) ( a – b ) = a2 – b2
LHS = ( a + b ) ( a – b ) Starting with the left-hand side of the equation
LHS = a2 – ab + ab + b2 Multiplying each term
LHS = a2 – b2
LHS = RHS
Visual Proof of ( a + b ) ( a – b ) = a2 – b2
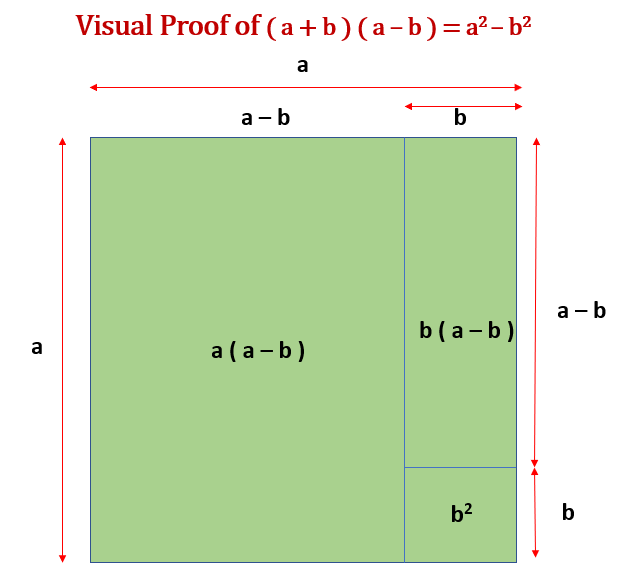
Proof: (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
LHS = (a + b + c)2 Starting with the left-hand side of the equation
LHS = ( a + b + c ) ( a + b + c )
LHS = a2 + ab + ac + ab + b2 + bc + ac + bc + c2 Multiplying each term
LHS = a2 + b2 + c2 + 2ab + 2bc + 2ac
LHS = RHS
Visual Proof of (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
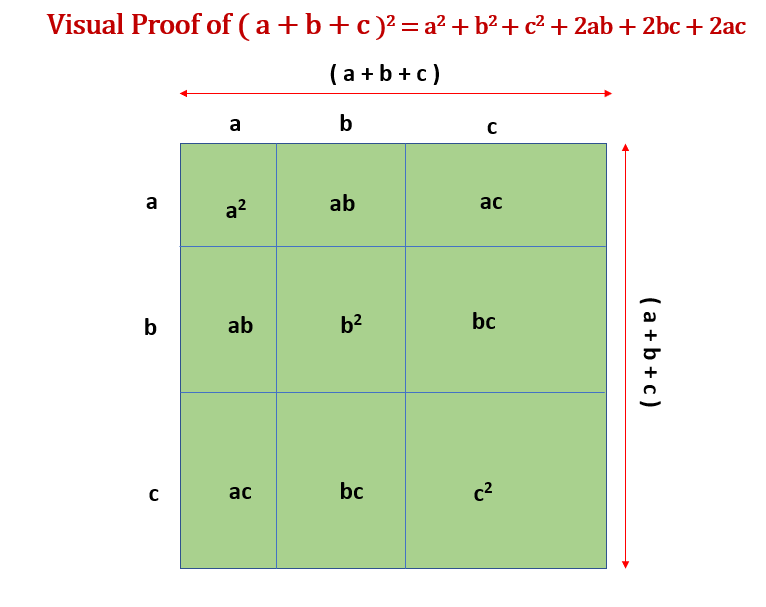
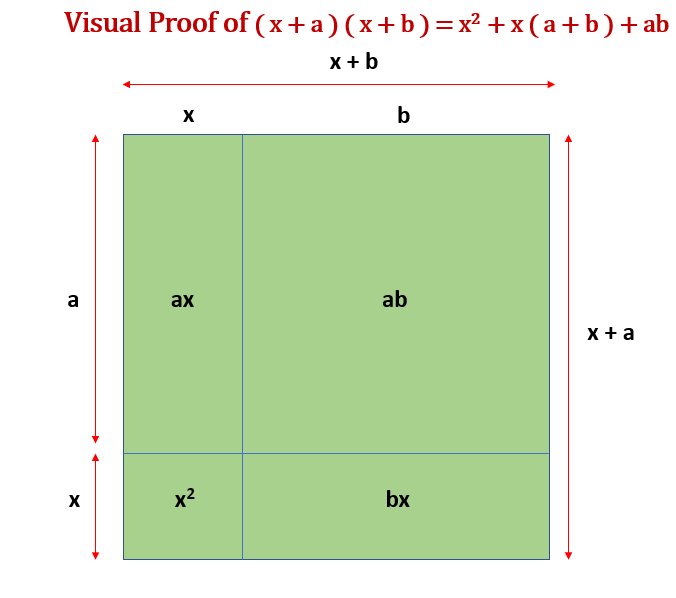
Proof: ( x + a ) ( x + b ) = x2 + x ( a + b ) + ab
LHS = ( x + a ) ( x + b ) Starting with the left-hand side of the equation
LHS = x2 + ax + bx + ab Multiplying each term
LHS = x2 + x ( a + b ) + ab Common Factor
LHS = RHS
Visual Proof of ( x + a ) ( x + b ) = x2 + x ( a + b ) + ab
Algebraic Identities for Two Variables a and b
The identities in algebra with two variables are as follows. These identities can be quickly confirmed by multiplying polynomials and extending the square or cube.
A. ( a + b )2 = a2 + 2ab + b2
B. ( a – b )2 = a2 – 2ab + b2
C. ( a + b ) ( a – b ) = a2 – b2
D. ( a + b )3 = a3 + 3a2 b + 3ab2 + b3
E. ( a – b )3 = a3 – 3a2 b + 3ab2 – b3
Examples
Example 1: Expand ( x + 7 )2.
Solution
Let us substitute a = x and b = 7 into the formula ( a + b )2 = a2 + 2ab + b2.
( x + 7 )2 = x2 + 2 ( x ) ( 7 ) + 72
( x + 7 )2 = x2 + 14x + 49
Example 2: Expand ( 3x + 2y )2.
Solution
Substituting a = 3x and b = 2y into the formula ( a + b )2 = a2 + 2ab + b2, we have,
( 3x + 2y )2 = ( 3x )2 + 2 ( 3x ) ( 2y ) + ( 2y )2
( 3x + 2y )2 = 9x2 + 12xy + 4y2
Example 3: Expand ( x – 3y )2.
Solution
Let us substitute a = x and b = 3y into the formula ( a – b )2 = a2 – 2ab + b2.
( x – 3y )2 = ( x )2 – 2 ( x ) ( 3y ) + ( 3y )2
( x – 3y )2 = x2 – 6xy + 9y2
Example 4: Expand ( 2x + 2y )3.
Solution
Substituting a = 2x and b = 2y into the formula ( a + b )3 = a3 + 3a2 b + 3ab2 + b3, we have,
( 2x + 2y )3 = ( 2x )3 + 3 ( 2x )2 ( 2y ) + 3 ( 2x ) ( 2y )2 +( 2y )3
( 2x + 2y )3 = 8x3 + 3 ( 4x2) ( 2y ) + 3 ( 2x ) ( 4y2) + 8y3
( 2x + 2y )3 = 8x3 + 24x2y + 24xy2 + 8y3
Example 5: Expand ( 3x – 4y )3.
Solution
Let us substitute a = 3x and b = 4y into the formula ( a – b )3 = a3 – 3a2 b + 3ab2 – b3, we have,
( 3x – 4y )3= ( 3x )3 – 3 ( 3x )2 ( 4y ) + 3 ( 3x ) ( 4y )2 – ( 4y )3
( 3x – 4y )3= 27x3 – 3 ( 9x2 ) ( 4y ) + 3 ( 3x ) ( 16y2) – ( 64y3 )
( 3x – 4y )3= 27x3 – 108x2y + 144xy2 – 64y3
Algebraic Identities for Three Variables a, b, and c
Just as the identities for the two variables, the identities for three variables in algebra have also been determined. Furthermore, using the fewest possible steps, these identities make it simple to work with algebraic expressions.
A. ( a + b + c )2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
B. a2 + b2 + c2 = ( a + b + c )2 – 2 ( ab + bc + ac )
C. a3 + b3 + c3 – 3abc = ( a + b + c ) ( a2 + b2 + c2 – ab – ac – bc )
D. ( a + b ) ( b + c ) ( c + a ) = ( a + b + c) ( ab + ac + bc ) – 2abc
Examples
Example 1: Expand ( x + 2y + 3z )2.
Solution
Let us substitute a = x, b = 2y, and c = 3z into the formula ( a + b + c )2 = a2 + b2 + c2 + 2ab + 2bc + 2ac.
( x + 2y + 3z )2 = ( x )2 + ( 2y )2 + ( 3z )2 + 2 ( x ) ( 2y ) + 2 ( 2y ) ( 3z ) + 2 ( x ) ( 3z )
( x + 2y + 3z )2 = x2 + 4y2 + 9z2 + 4xy + 12yz + 6xz
Example 2: Expand ( 3x + 4y + 2z )2.
Solution
Let us substitute a = 3x, b = 4y, and c = 2z into the formula ( a + b + c )2 = a2 + b2 + c2 + 2ab + 2bc + 2ac.
( 3x + 4y + 2z )2 = ( 3x )2 + ( 4y )2 + ( 2z )2 + 2 ( 3 x ) ( 4y ) + 2 ( 4y ) ( 2z ) + 2 ( 3x ) ( 2z )
( 3x + 4y + 2z )2 = 9x2 + 16y2 + 4z2 + 24xy + 16yz + 12xz
Factoring Identities
For quickly factoring algebraic expressions, algebraic identities are quite helpful. Some more complex algebraic expressions can easily be factored in using basic identities.
A. a2 – b2 = ( a – b ) (a + b )
B. a3 – b3 = ( a – b ) ( a2 + ab + b2 )
C. a3 + b3 = ( a + b ) ( a2 – ab + b2 )
D. x2 + x ( a + b ) + ab = ( x + a ) ( x + b )
Examples
Example 1: Factorize m4 – 81.
Solution
m4 – 81 = ( m2 )2 – ( 9 )2
m4 – 81 = ( m2 + 9 ) ( m2 – 9 )
m4 – 81 = ( m2 + 9 ) ( m – 3 ) ( m + 3 )
Example 2: Factorize p4 – ( q + r )4.
Solution
p4 – ( q + r )4 = ( p2 )2 – ( ( q + r )2 )2
p4 – ( q + r )4 = [ ( p2 + ( q + r )2 ] [ ( p2 – ( q + r )2 ]
p4 – ( q + r )4 = [ ( p2 + ( q + r )2 ] ( p + q + r ) ( p – q – r )
Example 3: Factorize n3 + 216.
Solution
Let us use the identity a3 + b3 = ( a + b ) ( a2 – ab + b2 ) where a = n and b = 6.
n3 + 216 = n3 + 63
n3 + 216 = ( n + 6 ) ( n2 – 6n + 36 )
Example 4: Factorize r3 – 64.
Solution
Let us use the identity a3 – b3 = ( a – b ) ( a2 + ab + b2 ) where a = r and b = 4.
r3 – 64 = r3 – 43
r3 – 64 = ( r – 4 ) ( r2 + 4r + 16 )
Summary
Algebraic identities are equations in which the right-hand side of the equation’s value is exactly equal to the left-hand side of the equation’s value. Any value for the variables satisfies them.
Algebraic Identities for Two Variables a and b
A. ( a + b )2 = a2 + 2ab + b2
B. ( a – b )2 = a2 – 2ab + b2
C. ( a + b ) ( a – b ) = a2 – b2
D. ( a + b )3 = a3 + 3a2 b + 3ab2 + b3
E. ( a – b )3 = a3 – 3a2 b + 3ab2 – b3
Algebraic Identities for Three Variables a, b and c
A. ( a + b + c )2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
B. a2 + b2 + c2 = ( a + b + c )2 – 2 ( ab + bc + ac )
C. a3 + b3 + c3 – 3abc = ( a + b + c ) ( a2 + b2 + c2 – ab – ac – bc )
D. ( a + b ) ( b + c ) ( c + a ) = ( a + b + c) ( ab + ac + bc ) – 2abc
Factoring Identities
A. a2 – b2 = ( a – b ) (a + b )
B. a3 – b3 = ( a – b ) ( a2 + ab + b2 )
C. a3 + b3 = ( a + b ) ( a2 – ab + b2 )
D. x2 + x ( a + b ) + ab = ( x + a ) ( x + b )
Frequently Asked Questions on Algebraic Identities ( FAQs )
What is meant by algebraic identities?
Algebraic identities are equations in which the right-hand side of the equation’s value is exactly equal to the left-hand side of the equation’s value. Any value for the variables satisfies them.
What are examples of standard algebraic identities?
The following are examples of some standard algebraic identities for variables a, b, and c.
| Algebraic Identities for Two Variables a and b |
| A. ( a + b )2 = a2 + 2ab + b2 B. ( a – b )2 = a2 – 2ab + b2 C. ( a + b ) ( a – b ) = a2 – b2 D. ( a + b )3 = a3 + 3a2 b + 3ab2 + b3 E. ( a – b )3 = a3 – 3a2 b + 3ab2 – b3 |
| Algebraic Identities for Three Variables a, b, and c |
| A. ( a + b + c )2 = a2 + b2 + c2 + 2ab + 2bc + 2ac B. a2 + b2 + c2 = ( a + b + c )2 – 2 ( ab + bc + ac ) C. a3 + b3 + c3 – 3abc = ( a + b + c ) ( a2 + b2 + c2 – ab – ac – bc ) D. ( a + b ) ( b + c ) ( c + a ) = ( a + b + c) ( ab + ac + bc ) – 2abc |
| Factoring Identities |
| A. a2 – b2 = ( a – b ) (a + b ) B. a3 – b3 = ( a – b ) ( a2 + ab + b2 ) C. a3 + b3 = ( a + b ) ( a2 – ab + b2 ) D. x2 + x ( a + b ) + ab = ( x + a ) ( x + b ) |
How do we verify algebraic identities?
The substitution approach is used to confirm the algebraic identities. Use the values in place of the variables in this method, then carry out the arithmetic operation.
How do we prove that an equation is an identity?
Applying known identities to show that one side of an equation may be converted into the other is necessary to establish an equation’s identity. To demonstrate that an equation is not an identity, we must identify one input where the values of the two sides of the equation disagree.
The following are examples of identity equations.
( x + 5 )2 = x2 + 10x + 25
( a – 4 )2 = a2 – 8a + 16
Notice that if we try to substitute values to the variables, the left-hand side is equal to the right-hand side of the equation.
On the other hand, these are examples of equations that are conditional.
4x = 32
x + 2 = 10
Notice that for both equations, only x = 8 will make the equations true. If we try to use other values, the left-hand side will not be equal to the right-hand side of the equation.
What is the importance of algebraic identities?
A fundamental group of mathematical formulas is algebraic identities. They assist you in carrying out calculations in quick, uncomplicated steps and are the building blocks of algebra. Many mathematical operations must be performed to solve certain algebraic problems.
What is meant by algebraic proofs?
The logical justifications for an algebraic solution are displayed in an algebraic proof. When a problem is presented, the task is to demonstrate that the solution is correct.
What are some examples of algebraic identity proofs?
The following are examples of standard algebraic proofs.
Proof: ( a + b )2 = a2 + 2ab + b2
LHS = ( a + b )2 Starting with the left-hand side of the equation
LHS = ( a + b ) ( a + b )
LHS = a2 + ab + ab + b2 Multiplying each term
LHS = a2 + 2ab + b2
LHS = RHS
Proof: ( a – b )2 = a2 – 2ab + b2
LHS = ( a – b )2 Starting with the left-hand side of the equation
LHS = ( a – b ) ( a – b )
LHS = a2 – ab – ab + b2 Multiplying each term
LHS = a2 – 2ab + b2
LHS = RHS
Proof: ( a + b ) ( a – b ) = a2 – b2
LHS = ( a + b ) ( a – b ) Starting with the left-hand side of the equation
LHS = a2 – ab + ab + b2 Multiplying each term
LHS = a2 – b2
LHS = RHS
Proof: (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ac
LHS = (a + b + c)2 Starting with the left-hand side of the equation
LHS = ( a + b + c ) ( a + b + c )
LHS = a2 + ab + ac + ab + b2 + bc + ac + bc + c2 Multiplying each term
LHS = a2 + b2 + c2 + 2ab + 2bc + 2ac
LHS = RHS
Recommended Worksheets
Algebraic Identities (World Environment Day Themed) Math Worksheets
Algebra (Rosh Hashanah Themed) Math Worksheets
Formulas (National Aviation Day Themed) Math Worksheets









