WHAT IS A PROPORTION?
A proportion is a mathematical statement that says two ratios are equal. It is an equality of two equivalent ratios denoted by the symbols “: : “ or “=”.
Mathematically, a proportion is defined as having four quantities a, b, c, and d such that the ratio a : b is equal to the ratio of c : d. Thus, we can express it as either a: b : : c : d, $\frac{a}{b}=\frac{c}{d}$ or a : b = a : c.
There are only terms you need to remember in proportions – the means and the extremes.
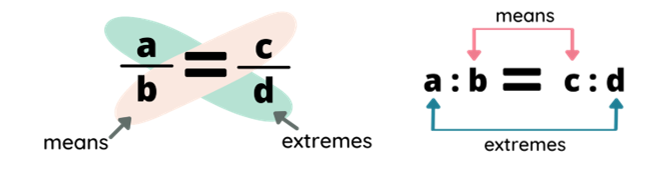
The means of the proportion are the terms close to each other when written in the form a: b : : c : d or a : b = a : c. When proportion is written in a fraction form $(\frac{a}{b}=\frac{c}{d})$, the means are the values hit by a diagonal drawn from the bottom left to the top right. Thus, the means are b and c.
The extremes of the proportions are the terms that is far from each other when written in the form a: b : : c : d or a : b = a : c. But when proportion is written in a fraction form, the extremes are the terms hit by a diagonal drawn from the top left to the bottom right. Thus, the extremes are a and d.
HOW DOES PROPORTION DIFFER FROM RATIO?
Ratio and proportion are closely related concepts. A ratio is a quotient of two quantities of the same kind denoted by $\frac{a}{b}$ or a : b where $b\neq 0$. Proportion is the relation between two equivalent ratios. In a ratio, we have the terms antecedent and consequent to denote the first and second terms, respectively.
The table below shows the difference between ratio and proportion.
| RATIO | PROPORTION |
| – used to compare the measure of two things with the same unit. | – used to represent the relation of two ratios. |
| – can be expressed using a colon (:), a slash (/), or a vinculum (-). | – can be expressed using the double colon (: 🙂 or the equal symbol (=) |
| – a mathematical expression | – a mathematical equation |
HOW TO USE THE CROSS-PRODUCT RULE OF PROPORTION?
The Cross-Product rule of proportion, also known as the means-extremes property, states that the product of the means is equal to the product of the extremes. To do this, simply cross-multiply the terms of the means and the extremes, respectively. Thus,

The product of the means is represented by ad and the product of the extremes is represented by bc.
EXAMPLE #1
Determine the value of x in the proportion $\frac{4}{7}=\frac{x}{35}$.
SOLUTION
Using the cross-product rule,
$4\times 35=7\times x$
$140=7x$
$\frac{7x}{7}=\frac{140}{7}$
$x=20$
Therefore, the value of x that will make the proportion true is 20.
EXAMPLE #2
What should be the value of x in the proportion $17:x=85:95$?
SOLUTION
Step 1: Change the form of the proportion into a fraction form. Hence,
$\frac{17}{x}=\frac{85}{95}$
Step 2: Use the cross-product rule. Thus,
$17\times 95=x\times 85$
$1615=85x$
$\frac{85x}{85}=\frac{1615}{85}$
$x=19$
Therefore, $x=19$.
EXAMPLE #3
Find the value of x in the proportion $\frac{3}{4}=\frac{15}{x}$.
SOLUTION
By cross-product rule,
$3\times x=4\times 15$
$3x=60$
$\frac{3x}{3}=\frac{60}{3}$
$x=20$
Therefore, the value of x is must be 20.
EXAMPLE #4
What must be the value of x in the proportion $x:8=40:50$?
SOLUTION
Step 1: Change the form of the proportion into a fraction form. Hence,
$\frac{x}{8}=\frac{40}{50}$
Step 2: Use the cross-product rule. Thus,
$x\times50=8\times40$
$50x=320$
$\frac{50x}{50}=\frac{320}{50}$
$x=6.4$
Therefore, $x=6.4$.
HOW TO SOLVE WORD PROBLEMS INVOLVING PROPORTIONS?
To solve word problems involving proportions, consider the following steps to find the unknown quantity:
- Analyze the problem.
- Jot down all the given information.
- Write an equation using equivalent ratios.
- Substitute the given value to the equation.
- Use the cross-product rule to find the value of the unknown.
EXAMPLE #1
Eleonor is planning to make a cupcake. According to her, for every 2 eggs, there must be 1 cup of milk for better consistency of the batter. If she plans on using 6 eggs, how many cups of milk does she need?
SOLUTION
Step 1: As stated in the problem, for every 2 eggs, there must be 1 cup of milk. Translating it to ratio will result to 2:1
Step 2: Create a mathematical equation that describes the problem. Thus, we will have the proportion $2:1=6:x$ where x denotes the unknown value of milk for every 6 eggs.
Step 3: Use the cross-product rule. Since we have an equation that is in the colon form, change the form to fraction form first. Hence,
$\frac{2}{1}=\frac{6}{x}$
$2\times x=1\times 6$
$2x=6$
$x=3$
Therefore, Eleanor needs 3 cups of milk for every 6 eggs.
EXAMPLE #2
A tree that is 10 feet tall casts a shadow on the ground that is 4 feet long. If the shadow of an electric post is 10 feet long, what is the height of the electric post?

SOLUTION
Step 1: Translating the sentence “10 feet tall casts a shadow on the ground that is 4 feet long” will give us the ratio $10:4$. That is the height of a tree with respect to the length of the shadow created.
Step 2: Create a mathematical equation that describes the situation. Hence, we will have the proportion $10:4=x:10$ where x is the height of an electric post.
Step 3: Change the form of the proportion to fraction form. Thus,
$\frac{10}{4}=\frac{x}{15}$
Step 4: Use the cross-product rule.
$10\times 10=4\times x$
$100=4x$
$\frac{4x}{4}=\frac{100}{4}$
$x=25$
Therefore, the height of the electric post is 25 ft.
WHAT IS A CONTINUED PROPORTION?
Three quantities a, b, and c are said to be in a continued proportion if the ratio of the first and second term is equal to the ratio of the second and third term. Thus, if a, b, and c are in a continued proportion, then,
$a:b∷b:c$
By getting the product of the means and the extremes, it follows that
$b\times b=a\times c$
$b^{2}=ac$
Continued proportion is also known as mean proportional.
If b is mean proportional with a and c, then $b^{2}=ac$.
EXAMPLE #1
Find the mean proportion between 13 and 15.
SOLUTION
Use the formula $b^{2}=ac$ to determine the mean proportion. Thus, by substitution,
$b^{2}=13\times15$
$b^{2}=195$
$b=\sqrt{195}$
$b=13.96$
Therefore, the mean proportion between 13 and 15 is approximately 13.96.
EXAMPLE #2
If 12 is the mean proportion between 16 and a number y. What must be the value of y to make this statement true?
SOLUTION
Step 1: Since the value of the mean proportion is 12, derive a formula that represents the given situation. Thus,
$b^{2}=ac$
$b=\sqrt{ac}$
Step 2: Substitute the given information to the formula, $b=\sqrt{ac}$. Thus,
$b=\sqrt{ac}$
$12=\sqrt{16\times y}$
$(12)^{2}=(\sqrt{16 y})^{2}$
$144=16y$
$\frac{16y}{16}=\frac{144}{16}$
$y=9$
Therefore, the value of y must be 9.
WHAT ARE THE PROPERTIES OF PROPORTION?
The properties of proportion and its example is listed below:
- INVERTENDO
For four values a, b, c, and d that is non-zero,
If $a:b=c:d$, then $b:a=d:c$.
The invertendo property of proportion simply states that if two ratios are equal, their inverse ratios are also equal.
For example,
If $7:8=14:16$, then by invertendo, $8:7=16:14$.
- ALTERNENDO
For four terms a, b, c, and d that is non-zero,
If $a:b=c:d$, then $a:c=b:d$.
The alternendo property states that if the second and third terms interchange places, then the four terms are still in proportion.
For example,
If $4:9=12:27$, then by alternendo, $4:12=9:27$.
- COMPONENDO
For four terms a, b, c, and d that is non-zero,
If $a:b=c:d$, then $a+b:b=c+d:d$.
For example,
If $$, then by componendo,
$6+10:10=12+20:20$
$16:10=32:20$
- DIVIDENDO
For four terms a, b, c, and d that is non-zero,
If $a:b=c:d$, then $a-b:b=c-d:d$.
For example,
If $7:5=21:15$, then by dividendo,
$7-5:5=21-15:15$
$2:5=6:15$
- CONVERTENDO
For four terms a, b, c, and d that is non-zero,
If $a:b=c:d$, then $a:a-b=c:c-d$.
For example,
If $13:11=39:33$, then by convertendo,
$13:13-11=39:39-33$
$13:2=39:6$
- COMPONENDO-DIVIDENDO
For four terms a, b, c, and d that is non-zero,
If $a:b=c:d$, then $a+b:a-b=c+d:c-d$.
For example,
If $2:3=10:15$, then by componendo-dividendo,
$2+3:2-3=10+15:10-15$
$5:-1=25:-5$
WHAT ARE THE TYPES OF PROPORTION?
Proportions can be classified into two different types – direct and inverse proportion. The figure below visually describes the relation of the two quantities in a direct and inverse proportion.

DIRECT PROPORTION
Direct proportion or direct variation is a mathematical comparison of two quantities where their ratio equals a constant value. Direct proportion states that when one of the quantity increase, the other will also increase. Similarly, if one of the quantities decreases, the other quantity will also decrease. The relation between two quantities is often denoted using the symbol ∝ or ~. Thus, we can express the direct proportions as y∝x or y~x.
The formula for direct proportion states that if two variables x and y, where y is directly proportional x,
y = kx
where,
k is the constant of proportionality.
Some examples of direct proportion are:
- The distance traveled with respect to time, where speed is the constant of proportionality;
- The circumference of a circle is directly proportional to the diameter where π is the constant of proportionality; and
- The work done to the number of workers, where the rate is the constant of proportionality.
EXAMPLE #1
If 4 candies cost USD6, how many candies can you buy with $30?
SOLUTION
Step 1: Let x be the number of candies
Step 2: Write the proportional relationship between the number of candies and their cost. Thus,
$\frac{4}{6}=\frac{x}{30}$
$4\times 30=6x$
$120=6x$
$\frac{6x}{6}=\frac{120}{6}$
$x=20$
Therefore, you can buy 20 candies if you have $30.
EXAMPLE #2
Tahani is making lemonade juice for a party. She mixed 4 liters of water for every ten pieces of lemonade. How many liters of water does she need if she has 28 lemonades?
SOLUTION
Step 1: Let x be the number of liters of water needed.
Step 2: Write a proportional relationship between the number of liters of water to the number of lemonade. Hence,
$\frac{4}{10}=\frac{x}{28}$
$4\times28=10x$
$112=10x$
$\frac{10x}{10}=\frac{112}{10}$
$x=11.2$
Therefore, Tahani needs 11.2 liters of water.
EXAMPLE #3
y is directly proportional to x. If y = 30 and x = 40, what is the value of the constant of proportionality?
SOLUTION
Step 1: Derive a formula for k from the formula of direct proportion $y=kx$. Thus,
$y=kx$
$k=\frac{y}{x}$
Step 2: Substitute values of x and y. Hence,
$k=\frac{30}{40}$
$k=0.75$
Therefore, the constant of proportionality is 0.75.
EXAMPLE #4
A car needs 45 liters of gasoline to cover a distance of 220 kilometers. How many liters of gasoline does a car need to cover a distance of 1080 kilometers?
SOLUTION
Step 1: Let x be the number of liters of gasoline, and y be the distance
Step 2: Use the given information and substitute it to the formula of direct proportion. Thus,
$y=kx$
$220=k(45)$
$220=45k$
$\frac{45k}{45}=\frac{220}{45}$
$k=\frac{44}{9}$
Step 3: Find the value of x if y is 1080 kilometers. Thus,
$y=kx$
$1080=(\frac{44}{9})x$
$1080=\frac{44x}{9}$
$9720=44x$
$\frac{44x}{44}=\frac{9720}{44}$
$x=\frac{2430}{11}$
$x=220.90$
Therefore, the car needs at least 221 liters of gasoline to cover the distance of 1080 kilometers.
INVERSE PROPORTION
Two quantities are said to be inversely proportional if the value of one quantity increases, the other decreases. Similarly, if one value decreases, the other value increases. Inverse proportion also uses the symbol ∝ or ~ to show proportionality. Thus, the statement “y is inversely proportional to x” is mathematically written as y ∝ $\frac{1}{x}$ or y ~ $\frac{1}{x}$.
The formula for inverse proportion states that if two variables x and y, where y is directly proportional x,
$y=\frac{k}{x}$
where,
k is the constant of proportionality.
One example of inverse proportion is speed with respect to time, where distance is the constant of proportionality.
EXAMPLE #1
Jason drove a certain distance in 45 minutes with an average of 50 kilometers per hour. Meanwhile, Michael drove the same distance in 30 minutes. What was Michael’s average speed of driving?
SOLUTION
Step 1: Knowing that speed is inversely proportional with time, write a mathematical proportion that describes the situation. Then, find the constant of proportionality.
$s=\frac{d}{t}$
$50=\frac{d}{45}$
$d=50\times 45$
$d=2250$
Step 2: Since we are looking for the average speed Michael drove and we already know the constant of proportionality, then,
$s=\frac{d}{t}$
$s=\frac{2250}{30}$
$s=75$
Therefore, Michael is driving at an average speed of 75 kilometers per hour.
EXAMPLE #2
Thirty persons in a quarantine facility are provided with food supplies that will last them six days. If five people were transferred to a different quarantine facility, how long would the food supplies last them now?
SOLUTION
Step 1: Let y be the number of people in a quarantine facility and x be the number of days the food supply will last. Then, using the formula of inverse proportion,
$y=\frac{k}{x}$
$30=\frac{k}{6}$
Step 2: Compute for the constant of proportionality. Hence,
$k=30\times6$
$k=180$
Step 3: Since five people were transferred to a different quarantine facility, simply subtract 5 from 30. Thus, we only have 25 people in the quarantine facility.
Step 4: Solve for the number of days the food provision will last if only 25 people are in the quarantine facility. Using the same formula for inverse proportion where $k=180$, then:
$y=\frac{k}{x}$
$25=\frac{180}{x}$
$25x=180$
$\frac{25x}{25}=\frac{180}{25}$
$x=7.2$
Therefore, the food supply will last 7 days if there are 25 people in the quarantine facility.
EXAMPLE #3
y is inversely proportional to x. If $y=63$ and $x=7$, what is the constant of proportionality? Additionally, what will be the value of y if $x=3$?
SOLUTION
Step 1: Use the formula of inverse proportion to find the value of the constant of proportionality. Thus,
$y=\frac{k}{x}$
$63=\frac{k}{7}$
$k=63\times7$
$k=441$
Step 2: Solve for the y if $x=3$. Hence,
$y=\frac{441}{3}$
$y=147$
Therefore, the constant of proportionality is $k=441$ and the value of y when $x=3$ is 147.
WHAT IS A CONSTANT OF PROPORTIONALITY?
When two quantities are directly or inversely proportional to each other, their relation can be described as either $y=kx$ or $y=\frac{k}{x}$, where k determines how they are related. The value of k is known as the constant of proportionality.
The constant of proportionality is the constant value of the ratio between two proportional quantities. The value of the constant of proportionality depends if it is a direct or inverse proportion.
- If two quantities are directly proportional to each other such that, $y=kx$, then the value of the constant of proportionality is denoted by $y=\frac{k}{x}$.
- If two quantities are inversely proportional to each other such that, $y=\frac{k}{x}$, then the value of the constant of proportionality is denoted by $k=xy$.
Knowing the constant of proportionality helps us determine the rate of change and, at the same time, the type of proportion we are dealing with.
WHAT IS THE IMPORTANCE OF PROPORTION?
The concept of proportion can be applied to different fields such as geography, physics, architecture, dietetics, cooking and baking, etc. It allows us to adjust certain recipes based on the ratio of ingredients, determine the percent increase and percent decrease for price mark-ups, scale diagrams, etc.
Recommended Worksheets
Ratio and Proportion Worksheets
Using Ratios and Proportion
Solving Proportional Relationships Between Two Quantities 7th Grade Math Worksheets









