Introduction
Multiplying by 11 is an essential skill in the field of mathematics. It is a technique that students begin learning in elementary school and continue to use throughout their mathematical journey. This article will comprehensively explain multiplying by 11, including grade appropriateness, the math domain it belongs to, applicable Common Core standards, definition of the topic, key concepts, illustrative examples and real-life applications, practice tests, and frequently asked questions.
Grade Appropriateness
Multiplying by 11 is typically introduced in 3rd grade and reinforced in subsequent grades as students become more comfortable with multiplication tables. However, it is a skill that can be taught earlier if a student is ready and shows an aptitude for understanding the concept.
Math Domain
The concept of multiplying by 11 falls under the Number and Operations in Base Ten or NBT in the Common Core State Standards. It is an essential component of arithmetic and number sense.
Applicable Common Core Standards
Some of the relevant Common Core Standards for this topic include:
3.NBT.A.3: Multiply one-digit whole numbers by multiples of 10 in the range 10-90 (e.g., 9 × 80, 5 × 60) using strategies based on place value and properties of operations.
4.NBT.B.5: Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers using strategies based on place value and the properties of operations.
Definition of the Topic
Multiplying by 11 is the process of finding the product of a given number and the number 11. It is an essential multiplication skill that helps understand and solve more complex mathematical problems.
Key Concepts
Doubling: When multiplying a single-digit number by 11, the product is obtained by writing the number twice. For example, 3 × 11 = 33.
Adding digits: When multiplying a two-digit number by 11, the product is obtained by adding the two digits and placing the sum between them. For example, 24 × 11 = 2 (2+4) 4 = 264.
Carrying: If the sum of the digits in the previous concept is greater than 9, you must carry the 1. For example, 59 × 11 = 5 (5+9) 9 = 5(14)9 = 649.
Discussion with Illustrative Examples
Single-digit numbers
When multiplying single-digit numbers by 11, write the number twice.
Examples
7 × 11 = 77
8 × 11 = 88
Two-digit Numbers
When multiplying two-digit numbers by 11, add the given digits and place the sum between them.
Examples
13 × 11 = 1 (1+3) 3 = 143
25 × 11 = 2 (2+5) 5 = 275
36 × 11 = 3 (3+6) 6 = 396
Two-digit Numbers with Carrying
When the sum of the digits is greater than 9, carry the 1.
Examples
68 × 11 = 6 (6+8) 8 = 6 (14) 8 = 748
46 × 11 = 4 (4+6) 6 = 5 (0) 6 = 506
79 × 11 = 7 (7+9) 9 = 8 (6) 9 = 869
Examples with Solution
a. 3 × 11 = 33
b. 12 × 11 = 132

c. 57 × 11 = 627
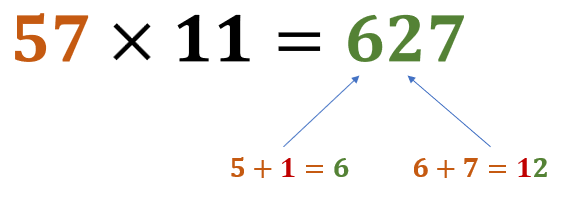
d. 75 × 11 = 825
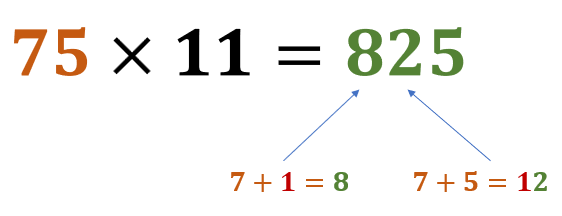
e. 89 × 11 = 979
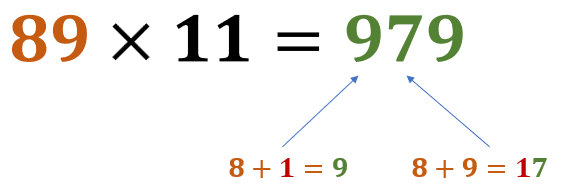
Real-life Application with Solution
Problem 1
Auntie sells sweet banana desserts. She bought 14 bunches of bananas. If there are 11 bananas in each bunch, how many did she buy?
Solution
Since we multiply two-digit numbers by 11, we must add the two digits and place the sum between them. So, we have,
14 × 11 = 1 (1+4) 4 = 154
Therefore, Auntie bought 154 bananas.
Problem 2
Suppose a store is having a sale with 11 items for $18. How much would it cost for 46 items?
Solution
First, find out how many sets of 11 items can be formed from 46 items.
46 ÷ 11 = 4 sets with a remainder of 2 items.
Now, multiply the cost of one set by the number of sets:
4 × $18 = $72
Since there are 2 items left, we need to find the cost per item. Divide the cost of one set by 11:
$18 ÷ 11 = $1.64 (approximately)
Now, multiply the cost per item by the remaining 2 items:
2 × $1.64 ≈ $3.28
Finally, add the costs together:
$72 + $3.28 ≈ $75.28
The cost for 46 items would be approximately $75.28.
Practice Test
1. 4 × 11 = ____
2. 23 × 11 = ____
3. 17 × 11 = ____
4. 91 × 11 = ____
5. 35 × 11 = ____
6. 62 × 11 = ____
7. 49 × 11 = ____
8. Mother bought six packs of chips at 11 dollars per pack. How much did Mother pay for these packs of chips?
Answers:
1. 4 × 11 = 44
2. 23 × 11 = 253
3. 17 × 11 = 187
4. 91 × 11 = 1001
5. 35 × 11 = 385
6. 62 × 11 =682
7. 49 × 11 = 539
8. 66 dollars
Frequently Asked Questions (FAQs)
Why is multiplying by 11 considered easy?
Multiplying by 11 involves simple techniques like doubling single-digit numbers or adding two digits together for two-digit numbers. These methods make it easier to find the product without memorizing the entire multiplication table.
Can these techniques be applied to larger numbers?
The techniques mentioned in this article can be applied to larger numbers but may require additional steps and adjustments.
What if the number has decimals?
If the number has decimals, you can still apply the techniques discussed in this article. However, remember to place the decimal in the correct position in the final product.
Are there any other techniques for multiplying by 11?
Yes, there are other techniques, like using the distributive property or the lattice method. However, the methods mentioned in this article are generally quicker and easier to apply.
Why is it important to learn to multiply by 11?
Multiplying by 11 is an essential math skill that helps understand and solve more complex mathematical problems. It also helps in improving mental math abilities and overall number sense.
Recommended Worksheets
Multiplying By 11 (Word Games Themed) Math Worksheets
Multiplying by 2 and 4 (Sherlock Holmes Themed) Math Worksheets
Multiplying By 5 & 25 (Budgeting Themed) Math Worksheets









