Count

Beginning at an early age, children begin to engage in the activity of counting different quantities. The main property of counting is so fundamental to our perception of quantity that it is rarely explicitly defined. Counting is the act of assigning a numerical value to a group of objects. So how can we count? By recognizing that such a value exists. Regardless of how we count, the result is always the same. Sometimes we count them twice to make sure we got the right number.

It cannot be overemphasized how important this is. We make a first step toward understanding mathematics by merely verbalizing it. From this fact alone, one can draw a number of conclusions.

• Rather than count two groups separately, we usually count one group first, followed by the other.
• There is only one thing that matters, and that is the quantity involved.
• Quantities are either described verbally or by number symbols (known as numerals), while variables are general terms used to describe unspecified quantities.

Although counting appears to be a simple concept, when you step back, there are actually a number of distinct counting principles that gradually help a child become capable of counting a group of objects. For children to be able to count well, they must learn five long-established counting principles. These principles include:

• Stable Order: Knowing and understanding the verbal sequence of counting; being able to say the number names sequentially
• One-to-One Correspondence: Understand that when the names of the numbers are sounded in sequence, no more than one count will be given for each object
• Cardinality: The idea that the last number spoken in a counting sequence represents the quantity for that set
• Abstraction: Recognizing that no matter what you count, how we count remains the same. As an example, any group of objects can be considered a set, regardless of whether they are the same color, shape, size, etc. It can also include non-physical things such as sounds and imaginary objects.
• Order Irrelevance: The order in which items are counted is irrelevant – from left to right, from right to left, or in a random order – as long as every object in the set is given one count and only one count   

What is Count?

We live with numbers and it is used in our everyday life. We use numbers to do many things, like counting socks to ensure you have matched pairs, counting the shoes in the shoe rack, counting the number of days in a week, counting the runs the India team made during the cricket match, counting the number of birds sitting on the building, etc.

Mathematics is heavily reliant on numbers. They are the building blocks of mathematics. Numbers are used for measuring and counting. They are fundamental to everyday life and mathematics. Everything we can count is a number.

Mathematically speaking, to count is to determine the quantity or the total number of objects in a group.

In other words, to count means to give value to items in a group based on one-to-one correspondence by saying numbers in order.

Counting numbers are used for counting objects.

As an example, the table also shows how we can count objects to ten using our fingers.

Reference: https://image.shutterstock.com/image-vector/illustration-set-number-1-10-600w-223671001.jpg

How to count?

Counting On – We can count by saying the numbers as we touch each object once. This is done by counting from a given number. This method is convenient when one of the addends is a small number like 1, 2, or 3.

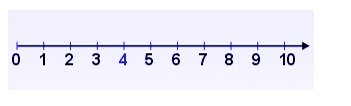
Reference: http://www.mathematicsdictionary.com/english/vmd/mirror/c/counton.gif

Counting Back – We can count backward by saying numbers in reverse order while touching each object once.

Beginning with a particular number, count backward the number of the previous number. It is the simplest way to find the difference when subtracting small numbers such as 1, 2, and 3.

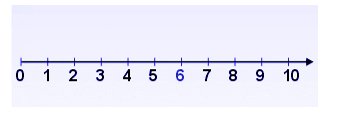
Reference: http://www.mathematicsdictionary.com/english/vmd/mirror/c/countback.gif

The Need for Simple Counting

In the course of human evolution, simply being able to recognize more or less, even or odd, etc., would be insufficient to meet the daily demands of living. As tribes and groups formed, it became critical to know how many members were in the group as well as how many were in the enemy’s camp. For them, knowing if the flock of sheep or other possessed animals was increasing or decreasing was very important.

It is often conjectured that one of the first methods of counting items would have been using tally sticks. These are objects that were used to count items. Using this method, each “stick” (or pebble, or whatever counting device is being used) represents one animal or object. The idea is that each item corresponds to one animal or object. The items that are being counted are uniquely linked to some counting tool in a one-to-one correspondence.

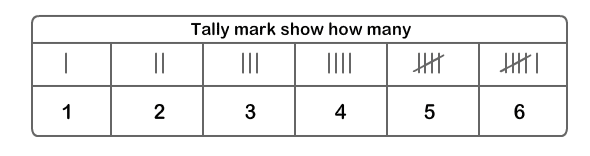
Reference: https://cdn.turtlediary.com/worksheets/question/count-animals-and-make-tally-chart.png

From the picture, one can imagine the usefulness of such a system, at least for smaller numbers of items to keep track of.

Our modern system has replaced sticks with more abstract objects. We replace the first stick with our symbol “1,” the second stick with a “2,” and the third stick with the symbol “3,”.

Introduction to Counting Numbers

Mathematics is a subject that is fundamentally concerned with counting. It all began with the necessity of counting. In the beginning, our ancestors counted with their fingers, and then they used beans, sticks, buttons, and beads. However, they realized later on that these methods of counting cannot be used in cases where we are forced to count large amounts of numbers. With the help of the fundamental counting principle, our mathematicians were able to find an efficient and accurate way to figure out large counts. The fundamental counting principle is one of the most important rules in Mathematics, especially when dealing with probability problems, as it is used to find the number of ways in which a combination of several events can occur.

Fun Facts about the Fundamental Principle of Counting:

• The Fundamental Principle of Counting can be extended to examples where there are more than two choices. It is possible for one event to happen in ‘x’ ways, another in ‘y’ ways, and another in ‘z’ ways, so all three can happen in x * y * z ways.
• The fundamental counting principle is also called the Counting Rule.
• When the same number of choices appear in several slots of a given fundamental counting principle example, then the exponent concept can be used to determine the answer.

Kinds of numbers

There are a lot of uses for numbers, including counting things and expressing magnitude. Mathematicians distinguish between two kinds of numbers: counting numbers and scalars.

Counting numbers: Natural numbers are all counting numbers. These numbers are always positive integers excluding 0. Numbers that can be counted between 1 and infinity form a very important part of the mathematical number system. Learning numbers begins in kindergarten. Everyday life relies on them as well.

Counting numbers written in a symbol from 1,2,3,….. are also called numerals. Numbers can also be written in words and are called number names.

Scalars: These are numbers that can be used to measure a quantity to any degree of accuracy. As an example, the height of a building is 10.422 meters, and the speed of an aircraft is 710.51 km/h. These numbers may have decimal parts or fractional parts. The types of numbers in this category include:

• Real numbers
• Imaginary or Complex Numbers
• Rational and Irrational numbers
• Integers
• Positive and negative numbers
• Prime and Composite numbers

Define Counting Numbers

As already discussed, mathematics defines counting as the act of determining the number or volume of objects contained in a group or set.

Counting numbers include even and odd numbers.

Example:

7 is an odd number and 8 is an even number. They are both counting numbers.

Different ways can be used to count the numbers, for example,

• Counting numbers by 2: 2,4,6,8,…
• Counting numbers by 3: 3,6,9,12,…
• Counting numbers by 4: 4,8,12,16,…
• Counting numbers by 5: 5,10,15,20,…
• Counting numbers by 6 and so on…

Facts About Counting Numbers

Any number can be used for counting things, i.e. 1,2,3,4,5,…..

Facts About Counting Numbers

• It does not include zero.
• It does not include fractions (such as 3/4,1/3….)
• It does not include negative numbers.
• It does not include decimals (such as 0.913, 2.37,….)
• Some people use commas in words when writing numbers, but some do not.
• In the beginning, human beings used their fingers to count numbers.
• Following million, billion, and trillion, a quadrillion, quintillion, sextillion, octillion, nonillion, decillion, and undecillion come.

Some Numbers That Are Not Considered Numbers

There are times when numbers are used as identifiers. Rather than quantifying something or counting it, they are used to label things in everyday life. An ID number, for example, is not used to measure anything. The ID is merely a string of digits that uniquely identifies a student. There is no point in trying to do arithmetic with them. In a similar fashion, a phone number’s square root has no meaning.

Progression of Count

It’s easy to take counting for granted, but there’s lots of fascinating research about how we learn to count – and there’s more to it than you may think.

Counting with toddlers

Researchers have found that toddlers – even as young as 12 months – understand how many objects are in a set – usually up to three. This is due to their innate ability to count.

The toddler learns how to count when he or she is able to connect the innate sense of “how many there are” to the language we use to describe things such as “one, two, buckle my shoe”. This is the start of learning math and it is the foundation for many early concepts.

Parents should use a variety of real objects to introduce their toddlers to the number system. Reading to your toddlers plays a crucial role in helping your child learn counting and language.

Counting – early learning milestones

From ages 3 to 5, you may notice your child going through the following stages of learning to count:

• Counting how many objects are in a small set without counting them. In other words, if you show your child four apples, they won’t have to count them to tell you there are four.

• Knowing the order of the “number words” from one to ten.

• Know the sequence regardless of which number they start on. By saying “start counting from four,” they will count “four, five . . .” instead of starting at 1.

• Children learn the principle of quantity conservation when they realize that if nothing is added or removed, the number of objects in a set stays the same. When you arrange six cans of beans in a straight line, and then rearrange them, say, into two stacks of three, they will realize there has to be six without counting them.

• You will soon discover that your child can count things that are not even visible to their eyes – such as sounds, members of another person’s family, or even ideas.

• Cardinality, not to be confused with carnality – The idea that the last number counted is equal to the quantity of the set. If your child counts 6 apples from 1,2,3,4,5,6 and then you ask “how many apples are there”? and they have to count again then they may not have grasped “cardinality”.

Counting on – as a step towards adding

Learning to add is an extension of learning to count. The following stages help a child connect these two concepts:

• Counting all – For 3 + 5, children will count, three fingers on one hand and five fingers on the other. The child will then count all the items “one, two, three, four, five, six, seven, eight”

• Counting on from the first number – Many children come to realize that it is unnecessary to count the first number when adding. They can start with three and then add another five to get the solution. The child will no longer count out the first set, but rather begin with the word ‘Three’, then use a hand to count out the second: ‘Four, five, six, seven, eight’.

• Counting on from the larger number – When the smaller of the two numbers is counted, it is more efficient. The child now selects the largest number, which is “five”, and counts “six, seven, eight”.

• The final stage is not really counting – When learners know their number facts, they can skip the time-consuming counting altogether.

The number line is an excellent visual aid that shows the connection between “counting on” and addition and subtraction.

Beyond basic counting

The first mathematical pattern learners encounter is counting. From here, they soon begin counting backward, which is the precursor to subtraction. They will also count in twos, fives, and tens, which prepares them for multiplication.

The next step is to introduce place value and count to base 10. This leap is often taken simply because it is an obvious and efficient method of counting large numbers.

It is easy to forget that counting is a major concept in math with many stages before it is mastered. There is certainly more to it than one, two, three!

Examples of Counting Numbers

Q.1. Is −5 a counting number?

Answer: No, −5 is not a counting number since counting numbers do not include negative numbers.

Q.2. Write all the odd counting numbers between 20 and 30.

Answer: The odd numbers between 20 and 30 are 21, 23, 25, 27, and 29.

Q.3. Is 0 a counting number?

Answer: No, 0 is not a counting number.

Q.4. Write the number name of 1,000,000 in the International system of numeration.

Ans: In the International System of Numeracy, 1,000,000 is called one million.

Q.5. What is the set of counting numbers?

Answer: Counting numbers are composed of a set of natural numbers.

Therefore, the set of counting numbers is {1,2,3,4,5,….}.

Q 6: Consider a scenario where a fair die is rolled and a card is drawn from a deck. How many outcomes are possible in this situation?

Answer: The total number of outcomes can be calculated by considering this example as one of the fundamental counting principle examples.

One can calculate the total number of outcomes from a die roll and a card drawing by multiplying the two numbers.

Assuming that a rolled die produces a number of outcomes of p and that a card from the deck produces a number of q, then the sum of the outcomes will be p x q.

A fair die has six faces. The total number of outcomes in the case of a die is p = 6.

A deck of cards has 52 cards. Therefore, there are 52 possible outcomes when a card is drawn.

Thus, when both events occur at the same time, the outcome is the product of p and q is 6 x 52 = 312.

Conclusion

Students who master the verbal counting sequence demonstrate an understanding of the stable order of numbers. Students can then use the counting sequence to count a set of objects using the various counting principles. Counting skills are considered a gateway to other mathematics skills, such as simple arithmetic to advanced mathematical concepts. Young students should be provided with multiple practice opportunities to show that they have an understanding and can apply skills to novel situations in the present and future.

References

1. https://shelleygrayteaching.com/counting-on/
2. https://byjus.com/maths/counting-numbers/
3. https://www.basic-math-explained.com/counting-numbers.html#.YVDPxrgzZPY
4. https://www.britannica.com/science/counting

Recommended Worksheets

Counting and Number Problems (National Poetry Day Themed) Math Worksheets
Counting Numbers (Basic) (Easter Themed) Math Worksheets
Understanding Fundamental Counting Principle and Probability of Events 7th Grade Math Worksheets
Counting Numbers 1-100 (by ones) Kindergarten Math Worksheets