Introduction
When we think of mathematics, the first thing that comes to our mind is numbers. We are aware of different kinds of numbers that have been defined such as natural numbers, whole numbers, decimal numbers, fractions and so on. But, how do we compose these numbers? Let us find out.
What are Numbers?
We use numbers in our day to day life. They are often called numerals. Without these numbers, it would be impossible to even count things. Different arithmetic operations can be performed using these numbers. But we don’t have just one set of numbers. There are a different sets of numbers such as whole numbers, natural numbers and so on. So, how do we define a number? A number is an arithmetic value used for representing the quantity and used in making calculations. For example, we have the number “ Four “ which in numeric form is written as “ 4 “. There are 10 digits, a combination of which is used to compose different numbers. These digits are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. These digits, other than 0 are called counting numbers. The system that is used to represent and compose these numbers is called the number system.
Decomposing Numbers from 1 to 5
Let us learn about decomposing numbers from 1 to 5.
How many balls can you see in the figure below?

It is 1 ball. 1 in words is written as One.
Now, how many balls can you see?
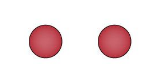
We have 2 = 1 + 1 . This is the next counting number after 1.
Again, how many balls are there?

We have 3 = 1 + 1 + 1 . This is the next counting number after 2.
From the above, we can see that 1 is the first counting number.
To decompose 2 from 1 we have to add 1 to itself, i.e. 2 is decomposed by 1 + 1.
Similarly, to decompose 3, we can add 1 to itself twice, i.e. 3 can be decomposed by 1 + 1 + 1
Another way to decompose 3 is by adding 1 to 2, i.e. 3 = 1 + 2
Now, let us decompose the number 4. There are three ways to compose the number 4.
How many balls do you see?
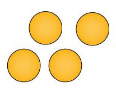
We have 4 = 1 + 1 + 1 + 1 = 1 + 2 + 1 = 1 + 3
Similarly, 5 = 1 + 1 + 1 + 1 + 1 = 1 + 3 + 1 = 2 + 3 = 1 + 4
Based on above, we can thus learn how to decompose numbers from 1 to 100.
Decomposing Numbers from 1 to 100
Starting from 1 and by incrementing each number by 1, we can form the numbers from 1 10 100 as below –
| 1 | 11 = 10 + 1 | 21 = 20 + 1 | 31 = 30 + 1 | 41 = 40 + 1 | 51 = 50 + 1 | 61 = 60 + 1 | 71 = 70 + 1 | 81 = 80 + 1 | 91 = 9 + 1 |
| 2 = 1 + 1 | 12 = 11 + 1 | 22 = 21 + 1 | 32 = 31 + 1 | 42 = 41 + 1 | 52 = 51 + 1 | 62 = 61 + 1 | 72 = 71 + 1 | 82 = 81 + 1 | 92 = 91 + 1 |
| 3 = 2 + 1 | 13 = 12 + 1 | 23 = 22 + 1 | 33 = 32 + 1 | 43 = 42 + 1 | 53 = 52 + 1 | 63 = 62 + 1 | 73 = 72 + 1 | 83 = 82 + 1 | 93 = 92 + 1 |
| 4 = 3 + 1 | 14 = 13 + 1 | 24 = 23 + 1 | 34 = 33 + 1 | 44 = 43 + 1 | 54 = 53 + 1 | 64 = 63 + 1 | 74 = 73 + 1 | 84 = 83 + 1 | 94 = 93 + 1 |
| 5 = 4 + 1 | 15 = 14 + 1 | 25 = 24 + 1 | 35 = 34 + 1 | 45 = 44 + 1 | 55 = 54 + 1 | 65 = 64 + 1 | 75 = 74 + 1 | 85 = 84 + 1 | 95 = 94 + 1 |
| 6 = 5 + 1 | 16 = 15 + 1 | 26 = 25 + 1 | 36 = 35 + 1 | 46 = 45 + 1 | 56 = 55 + 1 | 66 = 65 + 1 | 76 = 75 + 1 | 86 = 85 + 1 | 96 = 95 + 1 |
| 7 = 6 + 1 | 17 = 16 + 1 | 27 = 26 + 1 | 37 = 36 + 1 | 47 = 46 + 1 | 57 = 56 + 1 | 67 = 66 + 1 | 77 = 76 + 1 | 87 = 86 + 1 | 97 = 96 + 1 |
| 8 = 7 + 1 | 18 = 17 + 1 | 28 = 27 + 1 | 38 = 37 + 1 | 48 = 47 + 1 | 58 = 57 + 1 | 68 = 67 + 1 | 78 = 77 + 1 | 88 = 87 + 1 | 98 = 97 + 1 |
| 9 = 8 + 1 | 19 = 18 + 1 | 29 = 28 + 1 | 39 = 38 + 1 | 49 = 48 + 1 | 59 = 58 + 1 | 69 = 68 + 1 | 79 = 78 + 1 | 89 = 88 + 1 | 99 = 98 + 1 |
| 10 = 9 + 1 | 20 = 19 + 1 | 30 = 29 + 1 | 40 = 39 + 1 | 50 = 49 + 1 | 60 = 59 + 1 | 70 = 69 + 1 | 80 = 79 + 1 | 90 = 89 + 1 | 100 = 99 + 1 |
Now, that we have learnt how to decompose numbers from 1 to 100, we shall learn how to decompose larger numbers. But for that, it is important to understand the place value system.
What is Place Value System?
Place value is the basis of our entire number system. This is the system in which the position of a digit in a number determines its value. The place value of a digit in a number is the value it holds to be at the place in the number. Therefore, the number 65,471 is different from 17,645 because the digits are in different positions.
Importance of Place Value System in Composing Numbers
The usual way of writing numbers is a place value number system. Being familiar with place value allows us to put a number together given various place values of the number. Let us understand how this is done.
How are Numbers placed in the Place Value System?
Numbers, in a place value system, are placed according to their position in the place value chart. A place-value chart is a way to make sure digits are in the correct places. Let us understand how the place value chart is defined.
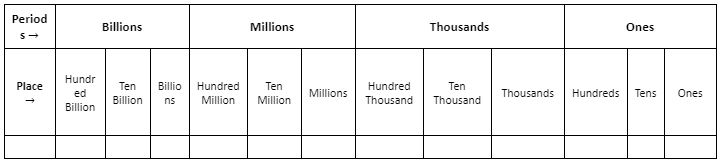
The place value chart of numbers is followed by most of the countries around the world. In this system, a number is split up into groups or periods. The following are the features of the International System of Numeration –
- We start from the extreme right digit of the number to form the groups.
- The groups are called ones, thousands, millions and billions.
- The ones, in turn, split up into hundreds, tens and units. The first three digits on the extreme right form a group of ones which in turn split into hundreds, tens and units.
- The second group of the next three digits on the left of the group of ones form the group of thousands which is further split into thousands, ten thousand and hundred thousand.
- The third group of the next three digits on the left of the group of thousands form the group of millions which is split into millions, ten million and hundred million.
- Three digits on the left of the group of millions form a group of billions which is split into billion, ten billion and hundred billion.
The place value chart of numbers is thus represented as –
From the place value system, we can say that
1 Million = 1000 thousand
1 Billion = 1000 Million
Let us understand this by an example.
Example
Write down the place of each digit in the number 845 and check the composition of the number.
Solution
We have been given the number 845. Let us obtain the place value of each digit of the given number.
The place value of 5 = 5 × 1 = 5
The place value of 4 = 4 × 10 = 40
The place value of 8 is 8 × 100 = 800.
This means that in order to compose the number 845, we will have
845 = 800 + 40 + 5
Let us see another example.
Suppose we want to check how the number 6847 has been composed. To understand this composition, we need to first understand the difference between place value and the face value of a number.
Place Value – The place value of a digit in a number is the value it holds to be at the place in the number.
Face Value – The face value of a digit in a number is the digit itself.
Now, we know that the place value of a digit depends on its position, whereas the face value does not depend on its position. For example, in the number six thousand eight hundred forty seven, i.e. 6847, the face value of 7 is 7. Similarly, the face values of 4, 8 and 6 are also, 4, 8 and 6 respectively. However, the digit –
7 has the place value 7 x 1 = 7, since it is in the units place
4 has the place value 4 x 10 = 40, since it is in the tens place
8 has the place value 8 x 100 = 800, since it is in the hundreds place
6 has the place value 6 x 1000 = 6000, since it is in the thousands place
In the expanded form, the number 6847 will be written as
6847 = 6 x 1000 + 8 x 100 + 4 x 10 + 7
It is evident from this that a number is the sum of the place values of all its digits.
Also, Place value of a Digit = Face Value x Position Value
However, it is important to note here that the place value of 0 is 0 itself, wherever it may be.
Now, that we have learnt how to decompose number, we should also learn how to decompose decimal numbers.
Decomposing Decimal Numbers
We know that decimal numbers are an extension of the natural numbers with values after the decimal point. To accommodate these values, the place value system of numbers has been extended as well for the decimal numbers.
Place Value System of Decimals
We know that each place in the place value table has a value ten times the value of the next place on its right. In other words, the value of a place is one-tenth of the value of the next place on its left. We observe that if one digit moves one place left to right its value becomes one-tenth ($\frac{1}{10}$ ) of its previous value and when it moves two places left to right its value comes one-hundredth ( $\frac{1}{100}$ ) of its previous term and so on. Therefore, if we wish to move beyond ones place which is the case of decimals, we will have to extend the place value table by introducing the places of tenths ($\frac{1}{10}$ ), hundredths ($\frac{1}{100}$ ), thousandths ( $\frac{1}{1000}$ ) and so on.
Therefore, the place value table in case of a decimal number will be of the form –
| Thousands( 1000 ) | Hundreds( 100 ) | Tens( 10 ) | Ones ( 1 ) | Tenths ($\frac{1}{10}$ ) | Hundredths ( $\frac{1}{100}$ ) | Thousandths ( $\frac{1}{1000}$ ) |
For example, the decimal number 257.32 in the place value system will be written as –
| Hundreds | Tens | Ones | Tenths | Hundredths |
| 2 | 5 | 7 | 3 | 2 |
Solved Examples
Example 1 Decompose the number as shown in the following figure –
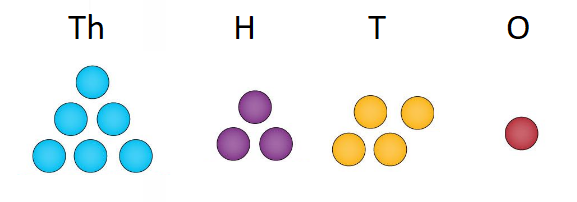
Solution Let us first write the face values of the corresponding digits in the given figure.
At the thousands place, we have 6, balls, which means that the face value of the number at the thousands place = 6
At the hundreds place, we have 3, balls, which means that the face value of the number at the hundreds place = 3
At the tens place, we have 4, balls, which means that the face value of the number at the tens place = 4
At the ones place, we have 1, balls, which means that the face value of the number at the ones place = 1.
Now, that we know that face values of each number, let us find the corresponding place values.
At the thousands place, since the face value is 6, therefore the place value will be 6 x 1000 = 6000
At the hundreds place, since the face value is 3, therefore the place value will be 3 x 100 = 300
At the tens place, since the face value is 4, therefore the place value will be 4 x 10 = 40
At the ones place, since the face value is 1, therefore the place value will be 1 x 1 = 1
Combining all the numbers we have,
6341 = 6000 + 300 + 40 + 1
Hence, the number represented in the given figure = 6341 = 6000 + 300 + 40 + 1
Example 2 Check whether we can decompose the number 110.235 to 70 + 40 + 0.2 + 0.03 + 0.005
Solution We have been given the expansion of number 110.235 and we need to check decompose it to see whether we can write it as 70 + 40 + 0.2 + 0.03 + 0.005
Referring to the place value system of decimals, first, we will add the two whole numbers given to us. We will have,
110.235 = 110 + 0.235 = 70 + 40 + 0.2 + 0.03 + 0.005
Hence, the decomposition of 110.235 can be 70 + 40 + 0.2 + 0.03 + 0.005
Key Facts and Summary
- A number is an arithmetic value used for representing the quantity and used in making calculations.
- The system that is used to represent and compose the numbers is called the number system.
- Place value is the basis of our entire number system. This is the system in which the position of a digit in a number determines its value.
- A place-value chart is a way to make sure digits are in the correct places. Let us understand how the place value chart is defined.
- The place value of a digit in a number is the value it holds to be at the place in the number.
- The face value of a digit in a number is the digit itself.
- Each place in the place value table has a value ten times the value of the next place on its right.
Recommended Worksheets
Decomposition of Numbers (Entomology Themed) Worksheets
Decomposing Fractions 4th Grade Math Worksheets
Decomposition of Numbers within 10 Kindergarten Math Worksheets









