Multiplying & Dividing Decimals by Powers of 10

What are Decimals?

The word decimal comes from the Latin word “Decem” which means 10. In algebra, a decimal number can be defined as a number whose complete part and the fractional part are separated by a decimal point. For example, 2.31, 4.07, 0.056 are all decimal numbers.

What do we mean by powers of 10?

Powers of 10 are used to show repeated multiplication or division by 10. They are used often to show very large or very small numbers. They can be written using exponents. For example, we can write 10 x 10 x 10 = 10³. Below we have a chart of powers of 10 that explains them further.

Number	10,000	1,000	100	10
Spoken	Ten thousand	One thousand	One hundred	Ten
Repeated Multiplication	10 x ( 10 x 10 x 10 )	( 10 x 10 x 10 )	10 x 10	10 x 1
Power	4	3	2	1
Exponential form	10 ⁴	10 ³	10 ²	10 ¹
Spoken	10 to the 4th power (Also referred to a 10 to the 4 or to the power 4 )	10 to the 3rd power	10 to the 2nd power	10 to the 1st power

Using Powers of 10 to represent large numbers

Powers of 10 can be similarly used to represent larger numbers. The below table demonstrates how large numbers can be expressed as powers of 10 –

Number	100,000,000,000	10,000,000	1,000,000	100,000
Spoken	One hundred million	Ten million	One million	One hundred thousand
Repeated Multiplication	10 x 10 x (10 x 10 x 10) x ( 10 x 10 x 10 )	10 x (10 x 10 x 10) x ( 10 x 10 x 10 )	( 10 x 10 x 10 ) x ( 10 x 10 x 10 )	( 10 x 10 ) x (10 x 10 x 10 )
Power	8	7	6	5
Exponential form	10 ⁸	10 ⁷	10 ⁶	10 ⁵
Spoken	10 to the 8th power	10 to the 7th power	10 to the 6th power	10 to the 5th power

Using Multiples of 10 to define Standard Form of Decimals

We know that a decimal consists of a whole number and a fractional part separated by a decimal. Before we understand how to write the decimals in their standard form, it is important to understand the decimal number system.

Decimal Place Value System

The decimal place value system is an extension of the number system of whole numbers that we have just learned. In this system, the digits of the fraction part have been defined according to their place values apart from the existing whole number writing system.

The Fractional part of the decimal is represented as –

Decimal (.)

Tenth

Hundredth

Thousandth

So, in a number 32.15 is the digit 1 is at the tenth place while the digit 5 is at the hundredth place. But, is this number in the standard form? Let us find out.

Standard Form of a decimal

By definition, any number that can be written as the decimal number, between the numbers 1.01.0 and 10.010.0, and then multiplied by the power of the number 10, is known to be in the standard form. For example, the number 5410000 in its standard form will be 5.4 x 10⁶.

How did we obtain this standard form?

It involves expressing a given decimal number by its first digit followed by a decimal point and its remaining digits, multiplied by a power of 10 such that it is equivalent to the original value.

Converting a decimal number into standard form

Converting a decimal number into standard form mostly just requires an understanding of the decimal place value system. We just need to multiply by the correct power of 10. We just need to use the following steps to rewrite a number in its standard form-

Power to the 10 shows the exact place of decimal to be moved.
To find the place of decimal you should first check whether the power is greater or less than 10.
If the power on 10 is greater than or equal to 10, the decimal point is moved to the left side. This case implies only if the power of 10 is positive. For example, 10².
If the power on 10 is lesser than 1, the decimal point is moved to the right side. This case implies only if the power of 10 is negative. For example, 10⁻².

Let us understand it with an example.

Example Write the number 650000 in its standard form.

Solution We have been given the number 650000. To convert this number in its standard form, we first count the number of digits after the first digit. We have 5 digits after the first digit, i.e. 6. Therefore, we will place a decimal after 6 and before 5 and multiply the given number by 10⁶. We will get 6.5 x 10⁶

Hence, the standard form of the number 650000 will be 6.5 x 10⁶.

Example Write the number 0.000568

Solution We have been given the number 0.000568. To convert this number in its standard form, we must first count the number of digits that lie between the decimal point and the first number from the left, i..e 5. The total number of digits is 4. We will, therefore, place a decimal between the first two numbers, other than 0, and multiply the number by 10^-4. We will get, 5.68 x 10^-4

Hence, the standard form of the number 0.000568 will be 5.68 x 10^-4

The standard form of decimal numbers is also known as scientific notation.

Multiplying Decimals by Powers of 10

It is important to understand that when multiplying by 10, the value of each digit increases 10 times and therefore moves one place to the immediate left. Multiplying by 100 increases the digits’ values by 100 times moving them two places to the left and multiplying by 1000 increases their value 1000 times and moves them three places to the left. Let us consider an example. Suppose we wish to multiply 7 by 10. We know that 7 x 10 = 70. Similarly 7 x 100 = 700 and 7 x 1000 = 7000. This can be represented using the place value system of numbers as –

Now let us consider a decimal number. There are similar patterns when multiplying both whole numbers and decimal numbers by powers of 10. Multiplying a decimal by 10 increases the value of each digit by 10. Multiplying a decimal by a power of 10 increases the value of each digit by a number of times that is equivalent to that power of 10. When a digit’s value is changed, that digit is moved to the appropriate place. This same effect can be realised by “moving the decimal point” but, as mentioned earlier, it is better to see the change in the value of the place in the digit is placed as representing the multiplication.

For instance, if we multiply the decimal number 2.43 by 10, we will have, 2.43 x 10 = 24.3. Similarly, 2.43 x 100 = 243 and 2.43 x 1000 = 2430. This can be represented using the place value system of numbers as –

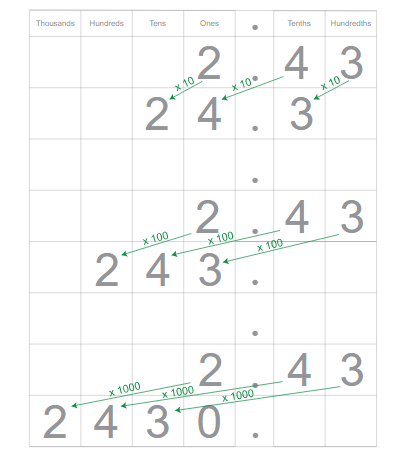
Let us now define the steps involved in multiplying decimal numbers as the power of 10.

Multiplication of decimal numbers by powers of 10 and representing them in scientific notation

The following steps are involved for the multiplication of numbers in scientific notations –

Obtain the decimal numbers in scientific notation.
Multiply the decimal numbers.
Multiply the powers of 10 by adding their exponents.
Convert your answer to scientific notation if necessary.

Let us understand the above steps using an example.

Example

Suppose we have two numbers ( 3 . 4 x 10 ^{– 2} ) and ( 6 . 2 x 10 ⁶ ) and we want to find their product.

Solution

We have been given two numbers ( 3 . 4 x 10 ^{– 2} ) and ( 6 . 2 x 10 ⁶ ) and we want to find their product. This means we need to find ( 3 . 4 x 10 ^{– 2} ) x ( 6 . 2 x 10 ⁶ ).

Going by the above defined steps, we need to first find the product of the decimal numbers in the scientific notation. We will have,

3 . 4 x 6 . 2 = 2 1 . 0 8 …………………………. ( 1 )

Next, we will multiply the powers of 10 for which we need to add the exponents of the two decimal numbers.

10 ^{– 2} x 10 ⁶ = 10 ^{– 2 + 6} = 10 ⁴ ………………………….. ( 2 )

Now, we will combine the results obtained in ( 1 ) and ( 2 ) to get,

( 3 . 4 x 10 ^{– 2} ) x ( 6 . 2 x 10 ⁶ ) = 2 1 . 0 8 x 10 ⁴

Finally, we will convert our result in scientific notation. We can see that we have 2 1 . 0 8 in our result which is greater than 1 and we know that for a number to be in scientific notation, its decimal number is at least 1 but less than 10. Therefore, we will move its decimal point one space to the left. Then, to keep the overall value the same, increase the exponent on the 10 by 1. We will then have,

2 1 . 0 8 x 10 ⁴ = 2 . 1 0 8 x 10 ⁵

Hence, ( 3 . 4 x 10 ^{– 2} ) x ( 6 . 2 x 10 ⁶ ) = 2 . 1 0 8 x 10 ⁵

Dividing Decimals by Powers of 10

Dividing whole numbers and decimal numbers by powers of 10 has the opposite effect to multiplying. The value of the digits decreases as opposed to increasing and the digits move to the right as opposed to the left on a place value chart. Let us, for example take the number 745 and divide it by 10. We will have 745 ÷ 10 = 74.5. Similarly, 745 ÷ 100 = 7.45 and 745 ÷ 1000 = 0.745

The above calculations can also be represented as –

745 ÷ 10¹ = 74.5	2,430 ÷ 10² = 2.43
745 ÷ 10² = 7.45	2,430 ÷ 10⁴ = 0.243
745 ÷ 10³ = 0.745	13,400 ÷ 10⁵ = 0.134
133 ÷ 10³ = 0.133	134,000 ÷ 10⁶ = 0.134
1,2300 ÷ 10⁵ = 0.123	1,340 ÷ 10⁴ = 0.134

Let us now define the steps involved in dividing decimal numbers as the power of 10.

Division of decimal numbers by powers of 10 and representing them in scientific notation

The following steps are involved for the division of numbers in scientific notations –

Obtain the decimal numbers in scientific notation.
Divide the decimal numbers.
Divide the powers of 10 by subtracting their exponents.
Convert your answer to scientific notation if necessary.

Let us understand the above steps using an example.

Example

Suppose we have two numbers ( 8 . 4 x 10 ⁵ ) and ( 1 . 4 x 10 ^{– 2} ) and we want to divide the first number by the second.

Solution

We have been given two numbers ( 8 . 4 x 10 ⁵ ) and ( 1 . 4 x 10 ^{– 2} ) and we want to divide the first number by the second. This means we need to find ( 3 . 4 x 10 ^{– 2} ) ÷ ( 6 . 2 x 10 ⁶ ).

Going by the above defined steps, we need to first divide the decimal numbers in the scientific notation. We will have,

8 . 4 ÷ 1 . 4 = 6 ………………….. ( 1 )

Next, we will divide the powers of 10 for which we need to subtract the exponents of the two decimal numbers. We will have,

( 10 ⁵ ) ÷ ( 10 ^{– 2} ) = 10 ^{( 5 – ( – 2 )} = 10 ^{5 + 2} = 10 ⁷ …………………………. ( 2 )

Now, we will combine the results obtained in ( 1 ) and ( 2 ) to get,

( 3 . 4 x 10 ^{– 2} ) ÷ ( 6 . 2 x 10 ⁶ ) = 6 x 10 ⁷

Finally, we will convert our result in scientific notation. We know that for a number to be in scientific notation, its decimal number is at least 1 but less than 10 and in our result, we have 6 in our result which is greater than 1 and less than 10. Therefore, our result is in scientific notation. Hence,

( 3 . 4 x 10 ^{– 2} ) ÷ ( 6 . 2 x 10 ⁶ ) = 6 x 10 ⁷

Rules for multiplying and dividing decimals by powers of 10

The rules pertaining to the operation of numbers in scientific notation can be summarised as

If the given number is multiples of 10 then the decimal point has to move to the left, and the power of 10 will be positive. For example 7000 can be written as 7 × 10 ³ is in scientific notation.
If the given number is smaller than 1, then the decimal point has to move to the right, so the power of 10 will be negative. For example the decimal number 0.0009 can be written as 9 × 0.0001 = 9 × 10 ^-4 is in scientific notation.

Key Facts and Summary

The word decimal comes from the Latin word “Decem” which means 10.
Powers of 10 are used to show repeated multiplication or division by 10. They are used often to show very large or very small numbers. They can be written using exponents.
If the given number is multiples of 10 then the decimal point has to move to the left, and the power of 10 will be positive.
If the given number is smaller than 1, then the decimal point has to move to the right, so the power of 10 will be negative.
When the scientific notation of any large numbers is expressed, then we use positive exponents for base 10.
When the scientific notation of any small numbers is expressed, then we use negative exponents for base 10.
When multiplying by 10, the value of each digit increases 10 times and therefore moves one place to the immediate left. Multiplying by 100 increases the digits’ values by 100 times moving them two places to the left and multiplying by 1000 increases their value 1000 times and moves them three places to the left.
Dividing whole numbers and decimal numbers by powers of 10 has the opposite effect to multiplying. The value of the digits decreases as opposed to increasing and the digits move to the right as opposed to the left on a place value chart.