Download Writing and Evaluating Algebraic Expressions Worksheets
Click the button below to get instant access to these premium worksheets for use in the classroom or at a home.

This worksheet can be edited by Premium members using the free Google Slides online software. Click the Edit button above to get started.
Download free sample
Not ready to purchase a subscription yet? Click here to download a FREE sample of this worksheet pack.
Definition:
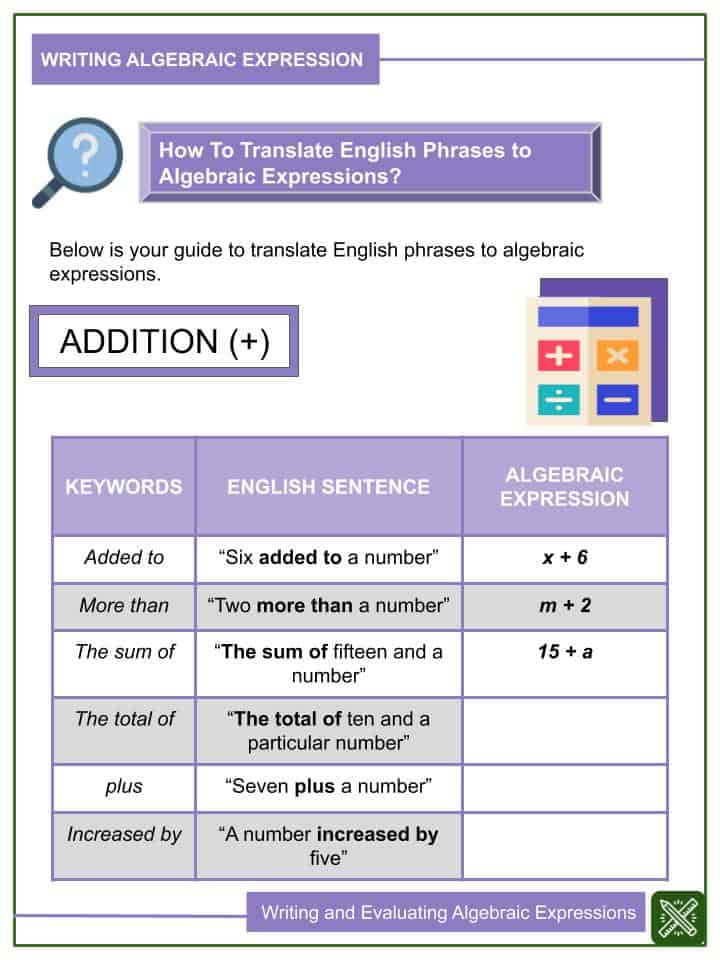
In mathematics, there are instances that the value of a certain number may be unknown. A variable is a symbol, usually a letter, used to represent an unknown number. A variable, a number, or a number and variable combined by multiplication or division is called a term. Meanwhile, a single term or a sum of two or more terms is called an algebraic expression.
Summary:
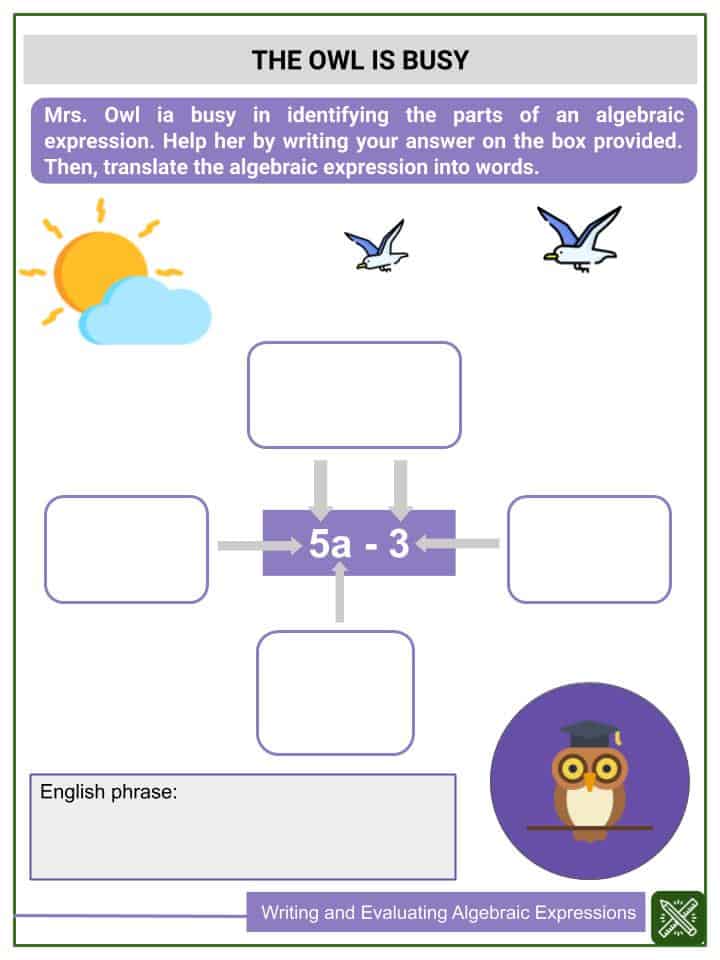
ENGLISH PHRASE: A number decreased by two.
ALGEBRAIC EXPRESSION: x – 2
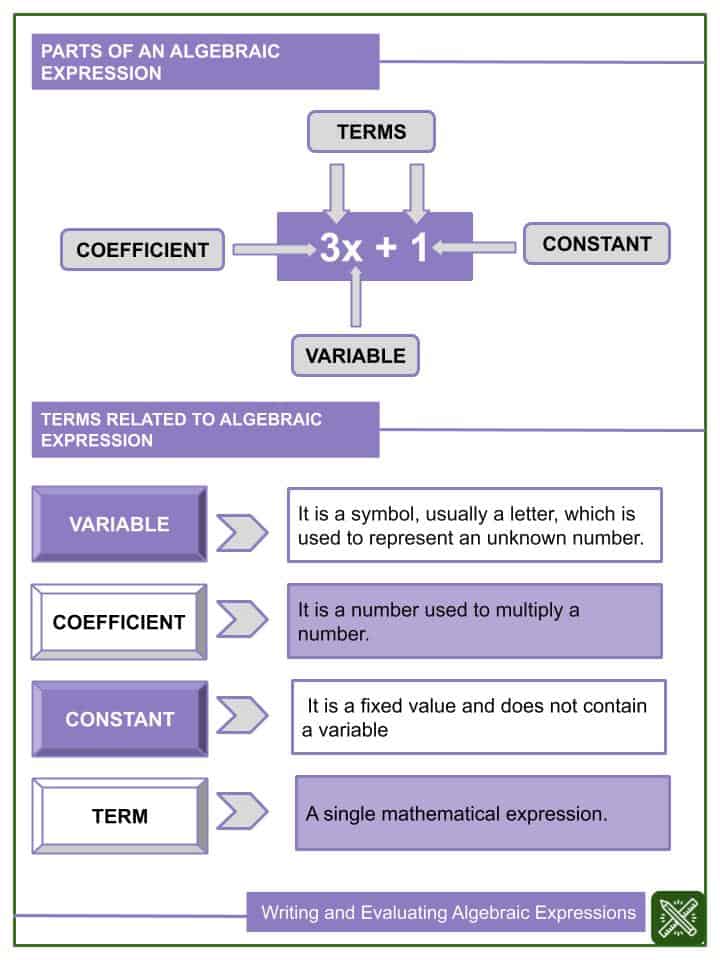
TERMS RELATED TO ALGEBRAIC EXPRESSION
- VARIABLE – It is a symbol, usually a letter, which is used to represent an unknown number.
- COEFFICIENT – It is a number used to multiply a number.
- CONSTANT – It is a fixed value and does not contain a variable.
- TERM – A single mathematical expression.
Writing and Evaluating Algebraic Expressions Worksheets
This is a fantastic bundle which includes everything you need to know about Writing and Evaluating Algebraic Expressions across 15+ in-depth pages. These are ready-to-use Common core aligned Grade 6 Math worksheets.
Each ready to use worksheet collection includes 10 activities and an answer guide. Not teaching common core standards? Don’t worry! All our worksheets are completely editable so can be tailored for your curriculum and target audience.
Resource Examples
Click any of the example images below to view a larger version.