The Volume of a Hollow Cylinder | Definition, Examples, Properties

Introduction

We frequently encounter solid shapes in our daily lives. We utilize, touch, and sense them. Objects with two dimensions: length and breadth are called 2D objects. A shape with three dimensions of length, breadth, and height is referred to as a three-dimensional shape or a solid shape. Solid shapes are also known as 3D shapes. By looking at them from various locations and angles, they appear to be distinct. The hollow cylinder is a 3-dimensional shape. The volume of the hollow cylinder is an important formula to be learned.

In this article first, we will learn what is a cylinder. Then we will understand what a hollow cylinder is. Next, we will study what volume is. Then, find formulas for the volume of a cylinder. Finally, we comprehensively discuss different formulas to calculate the volume of a hollow cylinder using examples.

What is a cylinder?

The cylinder is a three-dimensional shape with two parallel, round surfaces. These congruent circular surfaces could be either circles or ellipses. A curved side is also present. The axis of it is the separation between the centers of the bases. The circumference of the base makes up the width of the cylinder’s side, while the height of the cylinder makes up its length.

A cylinder has 2 bases, 3 faces (2 flat faces and 1 curved face), 2 edges and 0 vertices.

What are the typical examples of cylinder shapes?

Candle, Beaker, Water Tanks, Fire Extinguisher, Cold Drink Cans, Gas Cylinder, Battery, Pencil Holder, Cell, Oil Tank, Pencil, Dustbin, Log of Wood, Perfume/ Deodorant Bottle, Industrial Chimney, Drum, Cake

Properties of Cylinder

Equally parallel and congruent are the bases (flat faces).
Two of its edges are bent.
It has one face that curves.
It lacks verticals (specific corners).
Axis refers to the separation between the centers of the two bases.
The cylinder’s total surface area is made up of its bases and sides.
Space inside a cylinder makes up its volume.

Cylinder components

Base and Sides

A solid cylinder, like a straw, is a typical occurrence in daily life. A hollow cylinder can be broken down to reveal two bases, which are rather spherical closures. The bases all follow the same path and are identical. If you could ‘unroll’ the cylinder, you would notice that the side is a rectangular shape when it is straightened out.

Height

Height h is the distance between the two bases perpendicularly. It is essential to use the perpendicular height (sometimes known as “altitude”) when figuring out how much of a cylinder is inclined.

Radius

The radius r of a cylinder is the same as the base’s radius. Half of the diameter can be used to compute the radius.

Example:

Complete the below table.

Solution:

Now we will learn what is a hollow cylinder.

What is a hollow cylinder?

A cylinder can be visualized as a collection of stacked round disks. The distinction between a hollow cylinder and a cylinder, the cylinder is a solid surface created by a line travelling perpendicular to a fixed-line, with the end of the line describing a closed figure in a plane. A cylinder is considered to be hollow from the inside if there is some difference between the internal radius and external radius. A cylinder that has some discrepancy between the internal and external radius is called a hollow cylinder. In other words, a hollow cylinder is characterized as having a discrepancy between the internal and external radius and being empty on the inside. The hollow cylinder’s base is like an annular ring. So, the hollow cylinder’s bottom resembles an area encompassed by two concentric circles. In other words, two parallel cylindrical surfaces and two parallel circular bases, which are carved out of two parallel planes by these two cylindrical surfaces, are what make up a hollow cylinder. To put it another way, it is a cylinder that is hollow within and has some thickness at the edges.

What are the typical examples of hollow cylinder shapes?

Toilet paper roll, Water well, circular stadium, straws, bearing pushes

What is volume?

Understanding object volume is increasingly crucial for packing, storing, and transporting. Volume is a general term for the amount of space an object takes up which is a crucial parameter. Finding an object’s volume can help us calculate the quantity needed to fill it, such as the volume of water needed to fill a bottle, aquarium, or water tank. Cubic units are used to quantify an object’s volume.

Cubic centimetres – cm³

Cubic inches – in³

Cubic feet – ft³

Cubic meters – m³

What is the volume of a cylinder?

The density of a cylinder is determined by its volume, which represents how much material may be immersed in it or carried inside of it. The base area of a cylinder is the area of a cylinder’s round base. The cylinder’s base area can be used to calculate the volume of the cylinder. The volume of a cylinder is calculated by multiplying the base area of the cylinder by its height.

The volume of a cylinder=Base area of the cylinder × Height of the cylinder

Example:

Find the volume of the following cylinders.

Cylinder A with a base area of 14 cm² and a height of 10 cm
Cylinder B with a base area of 7 m² and a height of 10 m
Cylinder C with a base area of 21 ft² and a height of 10 ft

Solution:

The volume of cylinder A = Base area of cylinder A x Height of cylinder A=14 cm²×10 cm=140 cm³
The volume of cylinder B=Base area of cylinder B x Height of cylinder B=7 m²×10 m=70 m³
The volume of cylinder C=Base area of cylinder C x Height of cylinder C=21 ft²×10 ft=2100 ft³

If the base area of a cylinder is not given, we have to first calculate the base area of the cylinder to find the volume of the cylinder.

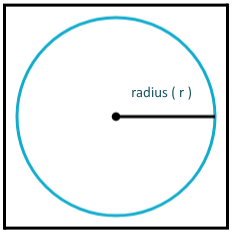
The base area of the cylinder could be calculated using the below formula.

The base area of the cylinder=π×radius²

The base area of the cylinder=π×r²

Steps to calculate the above formula.

The radius of the base of the cylinder should be calculated.
Find the radius’s square.
Multiply the radius’s square from π.
The answer is given in square units of the length radius.
- The result for the area is in cm² if the radius is specified in cm.
- The result for the area is in m² if the radius is specified in m.
- The result for the area is in ft² if the radius is specified in ft.

Example:

Find the base area of the following cylinders.

Cylinder A with a radius of 14 cm
Cylinder B with a radius of 7 m
Cylinder C with a radius of 21 ft

Solution:

The base area of cylinder A=π×(the radius of cylinder A)²=π×14 cm²=$\frac{22}{7}$ x (14 cm×14 cm=616 cm²
The base area of cylinder B=π×(the radius of cylinder B)²=π×7 m²=$\frac{22}{7}$ x (7 m×7 m=154 m²
The base area of cylinder C=π×(the radius of cylinder C)²=π×21 ft²=$\frac{22}{7}$ x 21 ft×21 ft=1,386 ft²

Now we know that,

The base area of the cylinder=π×radius²

Now, we can expand the formula of the volume of a cylinder.

The volume of a cylinder=Base area of the cylinder × Height of the cylinder=(π×radius²) x Height of the cylinder=π×r² x Height of the cylinder

Example:

Find the volume of the following cylinders.

Cylinder A with a radius of 14 cm and a height of 10 cm
Cylinder B with a radius of 7 m and a height of 10 m
Cylinder C with a radius of 21 ft and a height of 10 ft

Solution:

The volume of cylinder A = Base area of cylinder A × Height of cylinder A=π×The radius of cylinder A²×Height of cylinder A=π×14 cm²×10 cm = $\frac{22}{7}$ x 14 cm×14 cm×10 cm=6,160 cm³
The volume of cylinder B = Base area of cylinder B × Height of cylinder B=π×The radius of cylinder B²×Height of cylinder B=π×7 m²×10 m = $\frac{22}{7}$ x 7 m×7 m×10 m=1,540 m³
The volume of cylinder C=Base area of cylinder C×Height of cylinder C=π×The radius of cylinder C²×Height of cylinder C=π×21 ft²×10 ft = $\frac{22}{7}$ x 21 ft×21 ft×10 ft=13,860 m³

What is the volume of a hollow cylinder?

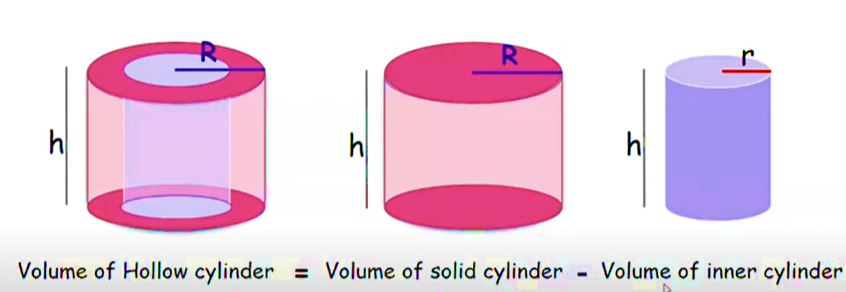
The volume of a hollow cylinder could be derived by using the formula for the volume of a cylinder. The volume of a hollow cylinder equals the difference between the volume of the external cylinder and the volume of the internal cylinder.

Formula 1 – The volume of a hollow cylinder

The volume of a hollow cylinder=The volume of the external cylinder-The volume of the internal cylinder

In other words, the volume of a hollow cylinder equals the difference between the volume of a solid cylinder and the volume of the inner cylinder.

The volume of a hollow cylinder=The volume of a solid cylinder-The volume of an inner cylinder

The above formula could be graphically presented as follows.

Example:

Find the volume of the following hollow cylinders.

Hollow cylinder A

The volume of the solid cylinder is 675 cm³ and the volume of the inner cylinder is 475 cm³

Hollow cylinder B

The volume of the solid cylinder is 50 m³ and the volume of the inner cylinder is 35 m³

Hollow cylinder C

The volume of the solid cylinder is 100 ft³ and the volume of the inner cylinder is 80 ft³

Solution:

The volume of hollow cylinder A=Solid cylinder’s volume of hollow cylinder A-Inner cylinder’s volume of hollow cylinder A=675 cm³-475 cm³=200 cm³
The volume of hollow cylinder B=Solid cylinder’s volume of hollow cylinder B-Inner cylinder’s volume of hollow cylinder B=50 m³-35 m³=15 m³
The volume of hollow cylinder C=Solid cylinder’s volume of hollow cylinder C-Inner cylinder’s volume of hollow cylinder C=100 ft³-80 ft³=20 ft³

We can determine the volume of the hollow cylinder if we know the base areas of the external (Solid) and interior (Inner) cylinders. We have to find the difference between the area of the external (Solid) cylinder and the internal (Inner) cylinder, and then multiply it by the height of the cylinders.

It can be demonstrated using the formula below.

Formula 2 – The volume of a hollow cylinder

The volume of a hollow cylinder=The base area of the external cylinder-The base area of the internal cylinder×Cylinder’s height

Example:

Find the volume of the following hollow cylinders.

Hollow cylinder A

The base area of the solid cylinder is 675 cm², the base area of the inner cylinder is 475 cm², and the height of the cylinder is 10 cm

Hollow cylinder B

The base area of the solid cylinder is 50 m², the base area of the inner cylinder is 25 m², and the height of the cylinder is 10 m

Hollow cylinder C

The base area of the solid cylinder is 100 ft², the base area of the inner cylinder is 80 ft², and the height of the cylinder is 10 ft

Solution:

The volume of hollow cylinder A=Solid cylinder’s base area of hollow cylinder A-Inner cylinder’s base area of hollow cylinder A×height of hollow cylinder A=675 cm²-475 cm²×10 cm=2,000 cm³
The volume of hollow cylinder B=Solid cylinder’s base area of hollow cylinder B-Inner cylinder’s base area of hollow cylinder B×height of hollow cylinder B=50 m²-25 m²×10 m=250 m³
The volume of hollow cylinder C=Solid cylinder’s base area of hollow cylinder C-Inner cylinder’s base area of hollow cylinder C×height of hollow cylinder C=100 ft²-80 ft²×10 ft=200 ft³

If the volume or base area of the external cylinder (Solid cylinder) and internal cylinder (inner cylinder) is not given, we have to find the volume of the external cylinder (Solid cylinder) and internal cylinder (inner cylinder) separately to find the volume of a hollow cylinder.

Let’s consider the radius of the external cylinder as “R”, the radius of the internal cylinder as “r” and the height of the hollow cylinder as “h”.

The volume of a hollow cylinder=The volume of the external cylinder-The volume of the internal cylinder

The volume of the external cylinder=The base area of the external cylinder x Height of the cylinder=π×(the radius of the external cylinder)² x Height of the cylinder=π×R²h

The volume of the internal cylinder=The base area of the internal cylinder x Height of the cylinder=π×(the radius of the internal cylinder)² x Height of the cylinder=π×r²h

Therefore,

Formula 3 – The volume of a hollow cylinder

The volume of a hollow cylinder=π×R²h-π×r²h

Example:

Find the volume of the following hollow cylinders.

Hollow cylinder A

The radius of the external cylinder is 14 cm, the radius of the internal cylinder is 7 cm, and the height of the cylinder is 10 cm

Hollow cylinder B

The radius of the external cylinder is 7 m, the radius of the internal cylinder is 3.5 m, and the height of the cylinder is 10 m

Hollow cylinder C

The radius of the external cylinder is 21 ft, the radius of the internal cylinder is 7 ft, and the height of the cylinder is 10 ft

Solution:

The volume of a hollow cylinder A=π×R²h-π×r²h=$\frac{22}{7}$ x 14 cm²×10 cm-$\frac{22}{7}$ x 7 cm²×10 cm=6,160 cm³-1,540 cm³=4,620 cm³
The volume of a hollow cylinder B=π×R²h-π×r²h=$\frac{22}{7}$ x 7 m²×10 m-$\frac{22}{7}$ x 3.5 m²×10 m=1,540 m³-385 m³=1,155 m³
The volume of a hollow cylinder C=π×R²h-π×r²h=$\frac{22}{7}$ x 21 ft²×10 ft-$\frac{22}{7}$ x 7 ft²×10 ft=13,860 ft³-1,540 ft³=12,320 ft³

Now, we will try to simplify the below formula and derive another formula to find the volume of a hollow cylinder.

The volume of a hollow cylinder=π×R²h-π×r²h

In the above formula, there are some common terms.

or$\frac{22}{7}$ is a common term for the volume calculation of the external cylinder of a hollow cylinder and the volume calculation of the internal cylinder of a hollow cylinder
h or height is also a common term for the volume calculation of the external cylinder of a hollow cylinder and the volume calculation of the internal cylinder of a hollow cylinder

Let’s consider π and height as common terms and rearrange the formula of the volume of a hollow cylinder.

Formula 4 – The volume of a hollow cylinder

The volume of a hollow cylinder=π×R²h – π×r²h=π×h×(R²-r²)

Example:

Find the volume of the following hollow cylinders using the below formula.

The volume of a hollow cylinder=π×h×(R²-r²)

Hollow cylinder A

The radius of the external cylinder is 14 cm, the radius of the internal cylinder is 7 cm, and the height of the cylinder is 10 cm

Hollow cylinder B

The radius of the external cylinder is 7 m, the radius of the internal cylinder is 3.5 m, and the height of the cylinder is 10 m

Hollow cylinder C

The radius of the external cylinder is 21 ft, the radius of the internal cylinder is 7 ft, and the height of the cylinder is 10 ft

Solution:

The volume of a hollow cylinder A=π×h×(R²-r²)=$\frac{22}{7}$×10 cm×(14 cm²-7 cm²)=$\frac{22}{7}$×10 cm x 147 cm²=4,620 cm³
The volume of a hollow cylinder B=π×h×(R²-r²)=$\frac{22}{7}$×10 m×(7 m²-3.5 m²)=$\frac{22}{7}$×10 m x 36.75 m²=1,155 m³
The volume of a hollow cylinder C=π×h×(R²-r²)=$\frac{22}{7}$×10 ft(21 ft²-7 ft²)=$\frac{22}{7}$×10 ft x 392 ft²=12,320 ft³

Let’s try to find the volume of a hollow cylinder when the thickness of the hollow cylinder is given. Let’s consider the radius of the external cylinder as “R”, the radius of the internal cylinder as “r”, the thickness of the hollow cylinder as “t” and the height of the hollow cylinder as “h”.

The thickness of a hollow cylinder=The radius of the external cylinder-The radius of the internal cylinder t=R-r

We can rearrange above the formula as follows.

The radius of the internal cylinder=The radius of the external cylinder-Thickness of a hollow cylinder r=R-t

Now, we can modify the formula for the volume of the hollow cylinder using the above formula.

Formula 5 – The volume of a hollow cylinder

The volume of a hollow cylinder=π×h×(R²-r²)=π×h×(R²-(R-t)²)

Example:

Find the volume of the following hollow cylinders.

Hollow cylinder A

The radius of the external cylinder is 14 cm, the thickness of the hollow cylinder is 7 cm, and the height of the cylinder is 10 cm

Hollow cylinder B

The radius of the external cylinder is 7 m, the thickness of the hollow cylinder is 3.5 m, and the height of the cylinder is 10 m

Hollow cylinder C

The radius of the external cylinder is 21 ft, the thickness of the hollow cylinder is 14 ft, and the height of the cylinder is 10 ft

Solution:

The volume of a hollow cylinder A=π×h×(R²-(R-t)²)=$\frac{22}{7}$×10 cm×(14 cm²-14 cm-7 cm²)=$\frac{22}{7}$×10 cm x 147 cm²=4,620 cm³
The volume of a hollow cylinder B=π×h×(R²-(R-t)²)=$\frac{22}{7}$×10 m×(7 m²-7 m-3.5 m²)=$\frac{22}{7}$×10 m x 36.75 m²=1,155 m³
The volume of a hollow cylinder C=π×h×(R²-(R-t)²)=$\frac{22}{7}$×10 ft(21 ft²-21 ft-14 ft²)=$\frac{22}{7}$×10 ft x 392 ft²=12,320 ft³

Summary

The cylinder is a three-dimensional shape with two parallel, round surfaces. A cylinder that has some discrepancy between the internal and external radius is called a hollow cylinder. The volume of cylinder calculation method is important in calculating the volume of a hollow cylinder. The volume of a cylinder is calculated by multiplying the base area of the cylinder by its height. The volume of a hollow cylinder equals the difference between the volume of the external cylinder and the volume of the internal cylinder. Multiple formulas can be formed by extending and rearranging the fundamental formula for the volume of a hollow cylinder.
The volume of a hollow cylinder=The volume of the external cylinder-The volume of the internal cylinder
The volume of a hollow cylinder=The base area of the external cylinder-The base area of the internal cylinder×Cylinder’s height
The volume of a hollow cylinder=π×R²h-π×r²h
The volume of a hollow cylinder=π×h×(R²-r²)
The volume of a hollow cylinder=π×h×R²-(R-t)²

Recommended Worksheets

Volume of Cylinders, Cones, and Spheres (Sports Themed) Math Worksheets
Solid Shapes (Christmas Day Theme) Math Worksheets
Solving Word Problems Involving Volume of Cylinders, Cones, and Spheres 8th Grade Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!