Introduction
The lattice multiplication method is typically used when solving problems, including multiplying 2-digit by 2-digit numbers. However, it can also be applied when handling bigger multi-digit numbers.
The lattice multiplication method is also a helpful way to multiply since it gives students a model to use to check that the numbers are correctly aligned.
The lattice multiplication method will be explained in this article, along with examples to determine the product of two numbers.
What is Lattice Multiplication Method?
Definition
Lattice multiplication is used as an alternative method to long multiplication or the grid method. Lattice multiplication is frequently used in multiplying larger numbers.
The lattice multiplication method makes it easier to reduce big numbers to basic mathematical concepts. This method can assist students in visualizing the many procedures and improving their comprehension of how to multiply numbers.
When using the lattice method of multiplication, we multiply each number’s digits and enter the result in the corresponding box. To create the digits of our answer, add the diagonals together.
For an easy example, let us look at the examples below of multiplying one-digit numbers.
3 × 6 = 18
4 × 7 = 28
2 × 3 = 6
Drawing a square is the first step in the lattice multiplication method. Next, a diagonal line is drawn from the top right corner of the square to the bottom left corner on the opposite side.
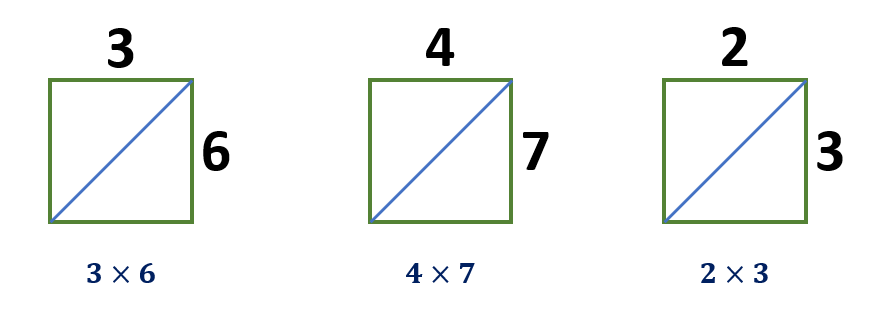
At the bottom right of the diagonal, we always write the ones or units of the answer. Any tens of the answers are always written in the upper left corner of the diagonal. If the answer does not contain any tens, zero is written to the left of the diagonal.

How do you solve using the lattice multiplication method?
For example, let us multiply 74 by 35 using the lattice multiplication method.
Step 1: Draw the lattice grid that matches the number of digits.
In this example, the factors 74 and 35 are 2-digit numbers; hence we will need a two × 2 lattice grid.
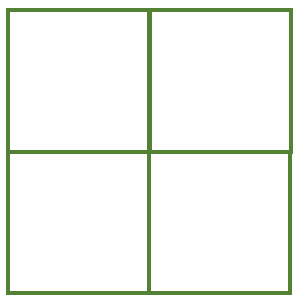
Step 2: Label the lattice grid by taking the first number on top and the second number on the right of the lattice.
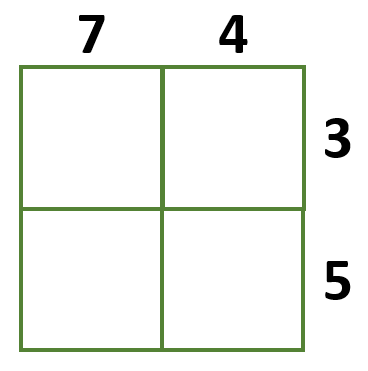
Step 3: Draw diagonal lines in each box. The lines must run from the bottom left corner of the boxes to the top right corner.
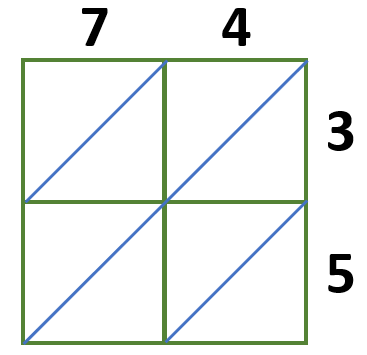
Step 4: Multiply each digit of the two numbers and write these answers in the corresponding boxes. The units are placed to the bottom right of the diagonal, while the tens are to the top left.
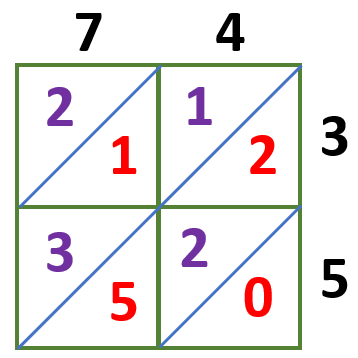
The product of the digits are as follows:
7 × 3 = 21
7 × 5 = 35
4 × 3 = 12
4 × 5 = 20
Step 5: Add up the numbers in each diagonal by starting at the right-hand side of the lattice grid. If the sum exceeds 9, carry over the tens digit to the next diagonal.
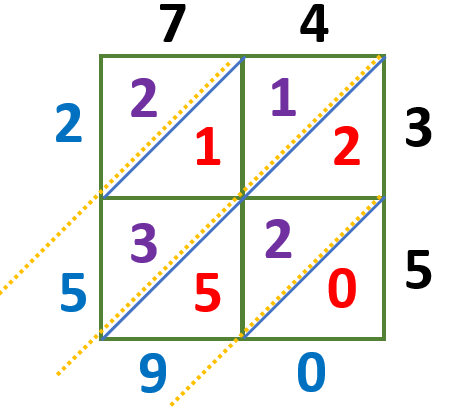
The sums of the numbers in each diagonal are as follows:
0 = 0
5 + 2 + 2 = 9
3 + 1 + 1 = 5
2 = 2
Step 6: Write the product starting from the number at the top left and ending with the bottom right number.
Therefore, when we multiply 74 by 35, the product is 2509.
74 × 35 = 2590
Lattice Multiplication Method Examples
2-digit by 2-digit Lattice Multiplication
Example 1
Using the lattice multiplication method, multiply 48 by 29.
Solution
In this example, we will need a 2 × 2 lattice grid since each factor has 2 digits.
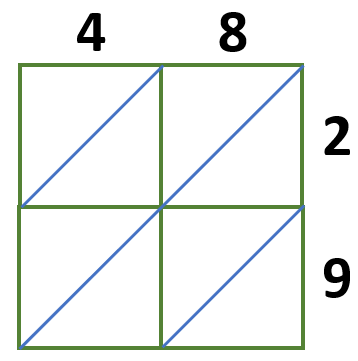
Multiply each digit of the two numbers and write these answers in the corresponding boxes we have,
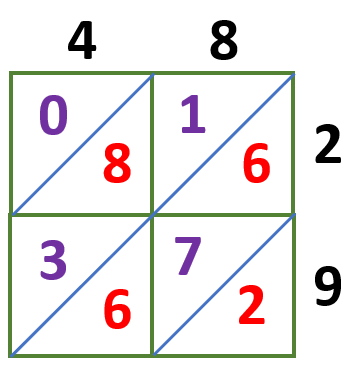
4 × 2 = 08
8 × 2 = 16
4 × 9 = 36
8 × 2 = 72
The units are placed to the bottom right of the diagonal, while the tens are to the top left.
Adding the numbers in each diagonal we have,
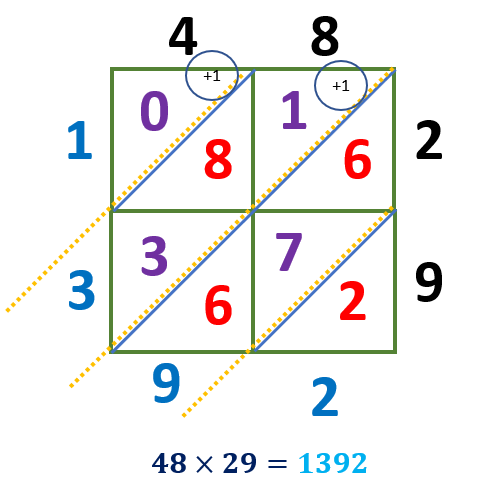
2 = 2
6 + 7 + 6 = 19
3 + 8 + 1 = 12
1 = 1
Since we have the sums 19 and 12, the tens digits are carried over to the next diagonal.
Write the product starting from the number at the top left and ending with the bottom right number. Hence, 48 × 92 = 1392.
Example 2
Multiply 87 by 24 using the lattice multiplication method.
Solution
In this example, we will need a 2 × 2 lattice grid since each factor has 2 digits.
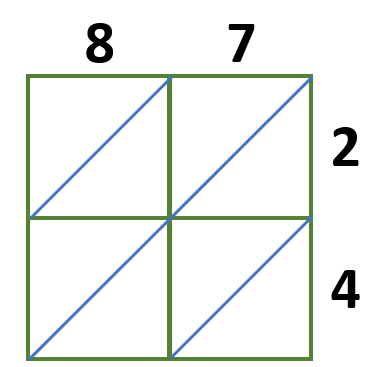
Multiply each digit of the two numbers and write these answers in the corresponding boxes we have,
8 × 2 = 16
7 × 2 = 14
8 × 4 = 32
7 × 4 = 28
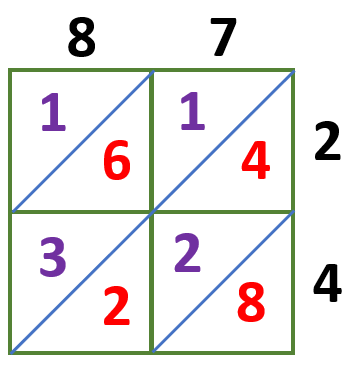
The units are placed to the bottom right of the diagonal, while the tens are to the top left.
As shown in the illustration below, adding the numbers in each diagonal we have,
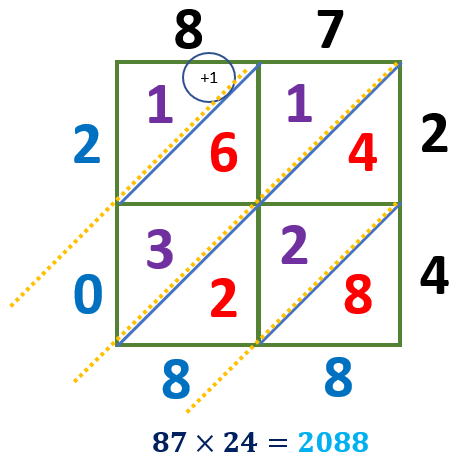
Since we have a diagonal with 10 as its total, the tens digit must be carried over to the next diagonal.
8 = 8
2 + 2 + 4 = 8
3 + 6 + 1 = 10
1+1 = 2
Write the product starting from the number at the top left and ending with the bottom right number. Thus, 87 × 24 = 2088.
Example 3
Find the product of 96 and 34 using the lattice multiplication method.
Solution
In this example, we will use a 2 × 2 lattice grid since each factor has 2 digits.
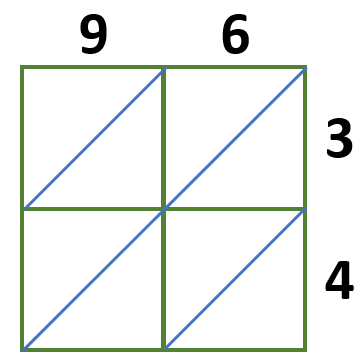
Multiply each digit of the two numbers and write these answers in the corresponding boxes we have,
9 × 3 = 27
6 × 3 = 18
9 × 4 = 36
6 × 4 = 24
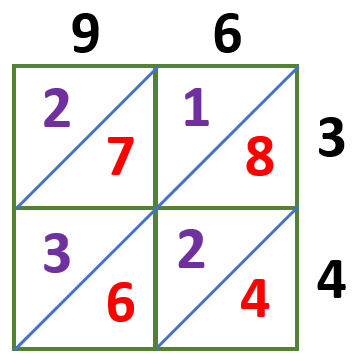
The units are placed to the bottom right of the diagonal, while the tens are to the top left.
The illustration below shows the adding the numbers in each diagonal.
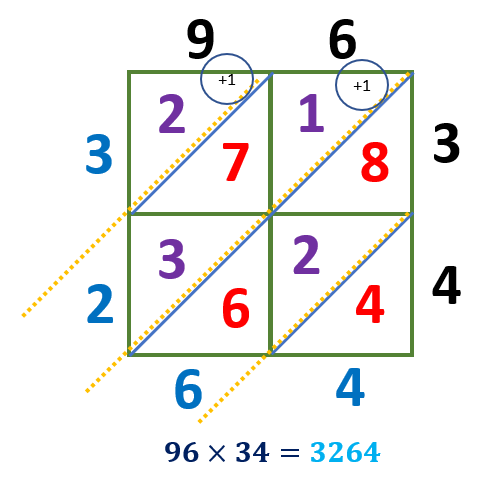
4 = 4
6 + 2 + 8 = 16
3 + 7 + 1 = 12
2 + 1 = 3
Since we have the sum 16 and 12, the tens digit must be carried over to the next diagonal.
Write the product starting from the number at the top left and ending with the bottom right number. Therefore, the product of 96 and 34 is 3264.
3-digit by 2-digit Lattice Multiplication
Example 1
Multiply 325 by 28 using the lattice multiplication method.
Solution
Since we are multiplying a 3-digit number by a 2-digit number, we will use a 3 × 2 lattice grid.
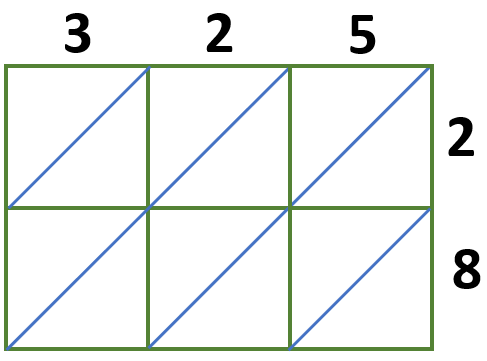
Multiply each digit and write these answers in the corresponding boxes we have,
3 × 2 = 06
2 × 2 = 04
5 × 2 = 10
3 × 8 = 24
2 × 8 = 16
5 × 8 = 40
The tens digits are written at the top left of the diagonal, while the ones digits are written at the bottom right, as shown below.
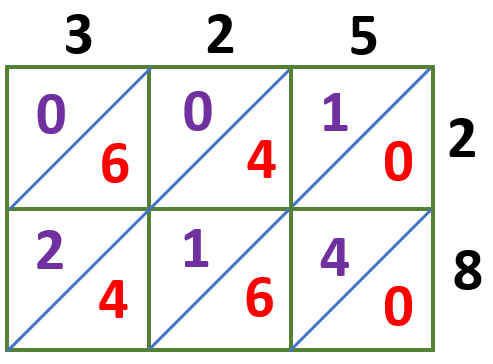
Let us now get the sum of the number in each diagonal starting from the lower right corner of the lattice grid.
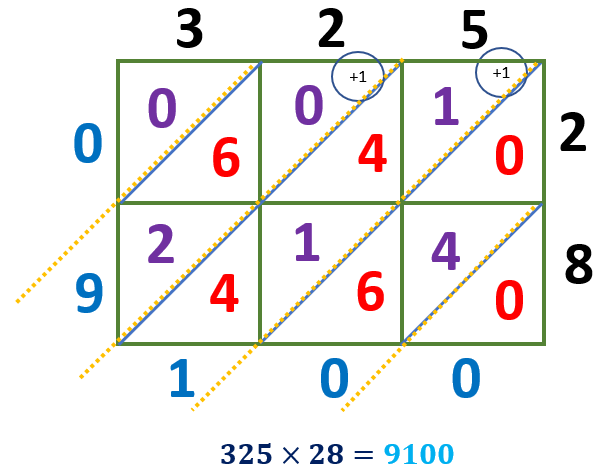
Since we have the sum 10 and 11, the tens digit must be carried over to the next diagonal.
0 = 0
6 + 4 + 0 = 10
4 + 1 + 4 + 1= 11
2 + 6 + 1 = 9
0 = 0
Write the answer starting from the number at the top left and ending with the bottom right number. Thus, the product of 325 and 28 is 9100.
Example 2
Using the lattice multiplication method, find 856 × 47.
Solution
We will use a 3 × 2 lattice grid since we multiply a 3-digit number by a 2-digit number.
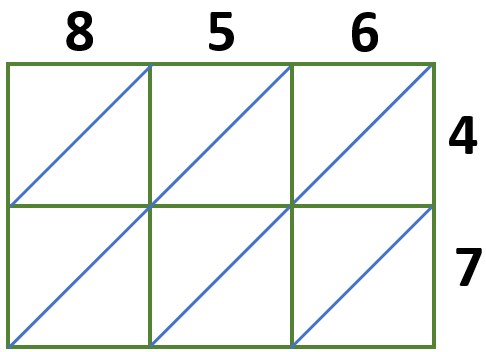
Multiply each digit and write these answers in the corresponding boxes we have,
8 × 4 = 32
5 × 4 = 20
6 × 4 = 24
8 × 7 = 56
5 × 7 = 35
6 × 7 = 42
The tens digits are written at the top left of the diagonal, while the ones digits are written at the bottom right, as shown below.
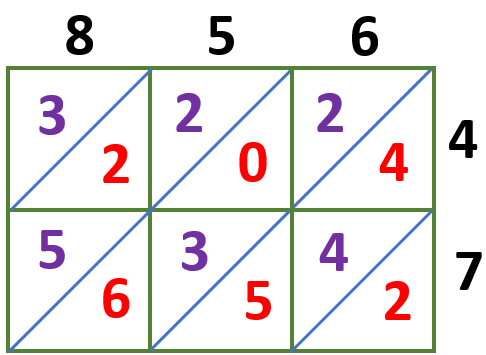
Let us now get the sum of the number in each diagonal starting from the lower right corner of the lattice grid.
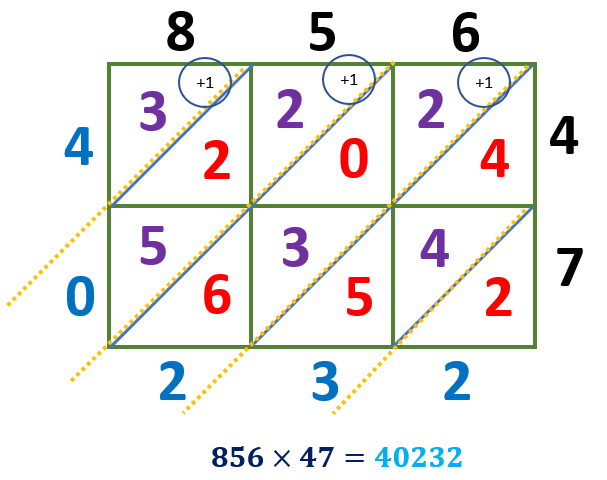
Since we have the sums 13, 12, and 10, the tens digit must be carried over to the next diagonal.
2 = 2
5 + 4 + 4 = 13
6 + 3 + 0 + 2 + 1 = 12
5 + 2 + 2 + 1 = 10
3 + 1 = 4
Write the product starting from the number at the top left and ending with the bottom right number. Thus, the product of 856 and 47 is 40232.
Example 3
Using the lattice multiplication method, show the product when 315 is multiplied by 83.
Solution
We will use a 3 × 2 lattice grid since we multiply a 3-digit number by a 2-digit number.
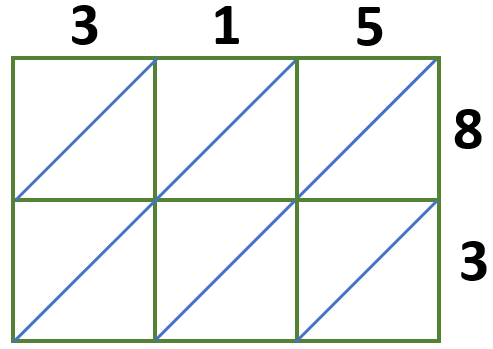
Multiply each digit and write these answers in the corresponding boxes we have,
3 × 8 = 24
1 × 8 = 08
5 × 8 = 40
3 × 3 = 09
1 × 3 = 03
5 × 3 = 15
The tens digits are written at the top left of the diagonal, while the ones digits are written at the bottom right, as shown below.
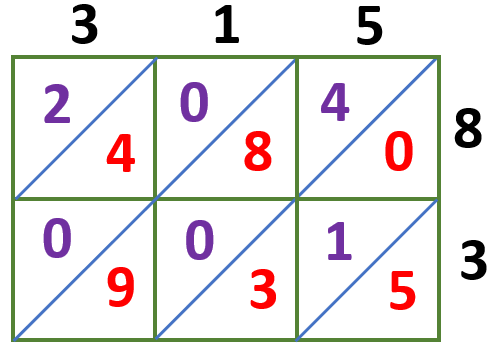
Let us now get the sum of the number in each diagonal starting from the lower right corner of the lattice grid.

Since we have the 21, the tens digit, 2, must be carried over to the next diagonal.
5 = 5
3 + 1 + 0 = 4
9 + 0 + 8 + 4 = 21
0 + 4 + 0 + 2 = 6
2 = 2
Write the product starting from the number at the top left and ending with the bottom right number. Thus, the product of 315 and 83 is equal to 26145.
3-digit by 3-digit Lattice Multiplication
Example 1
Using the lattice multiplication method, find 845 × 735.
Solution
We will use a 3 × 3 lattice grid since we multiply a 3-digit number by a 3-digit number.
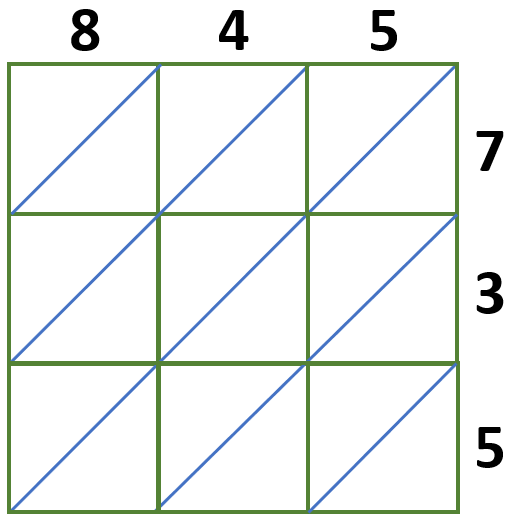
Multiply each digit and write these answers in the corresponding boxes we have,
8 × 7 = 56
4 × 7 = 28
5 × 7 = 35
8 × 3 = 24
4 × 3 = 12
5 × 3 = 15
8 × 5 = 40
4 × 5 = 20
5 × 5 = 25
The tens digits are written at the top left of the diagonal, while the ones digits are written at the bottom right of each box, as shown below.
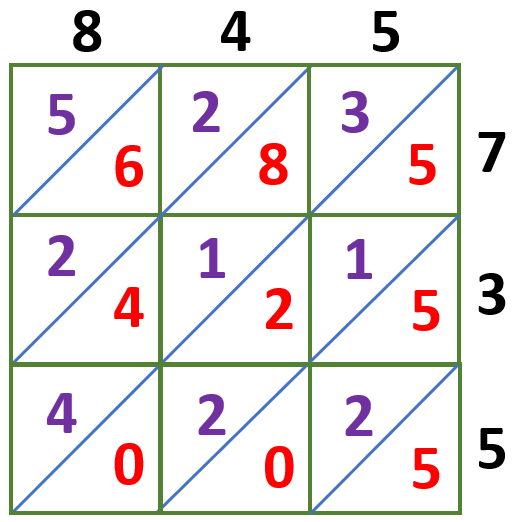
Let us now get the sum of the number in each diagonal starting from the lower right corner of the lattice grid.
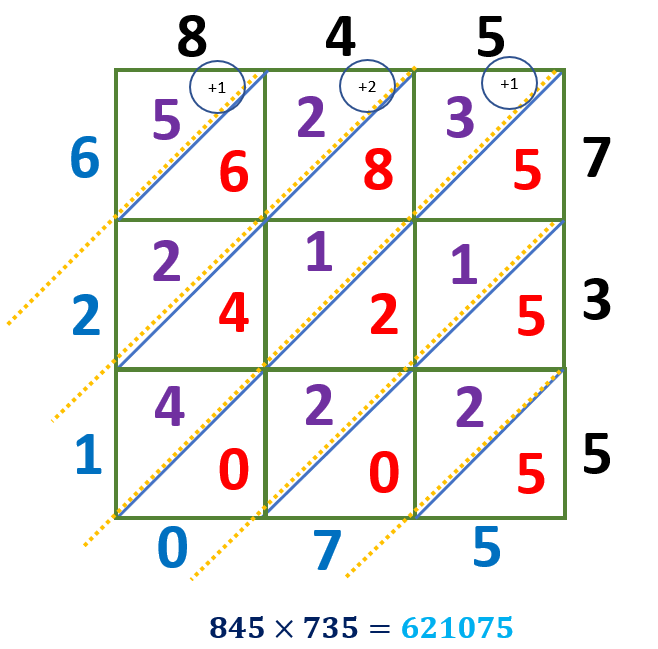
Since we have the 21, the tens digit, 2, must be carried over to the next diagonal.
5 = 5
0 + 2 + 5 = 7
0 + 2 + 2 + 1 + 5 = 10
4 + 4 + 1 + 8 + 3 = 21
2 + 6 + 2 + 2 = 12
5 + 1 = 6
Write the product starting from the number at the top left and ending with the bottom right number. Thus, the product of 845 and 735 is equal to 621075.
Example 2
Solve 986 × 279 using the lattice multiplication method.
Solution
We will use a 3 × 3 lattice grid since we multiply a 3-digit number by a 3-digit number.

Multiply each digit and write these answers in the corresponding boxes we have,
9 × 2 = 18
8 × 2 = 16
6 × 2 = 12
9 × 7 = 63
8 × 7 = 56
6 × 7 = 42
9 × 9 = 81
8 × 9 = 72
6 × 9 = 54
The tens digits are written at the top left of the diagonal, while the ones digits are written at the bottom right of each box, as shown below.
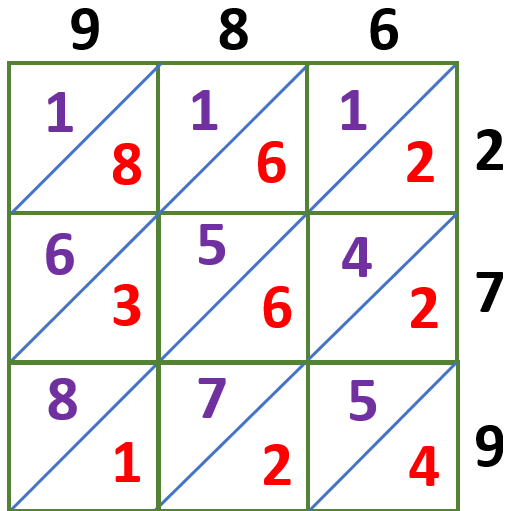
Let us now get the sum of the number in each diagonal starting from the lower right corner of the lattice grid.
As shown below, we have the sums 20, 25, and 17, the tens digits, which must be carried over to the next diagonal.

4 = 4
2 + 5 + 2 = 9
1 + 7 + 6 + 4 + 2 = 20
8 + 3 + 5 + 6 + 1 + 2 = 25
6 + 8 + 1 + 2 = 17
1 + 1 = 2
Write the product starting from the number at the top left and ending with the bottom right number. Thus, the product of 986 and 279 is equal to 275094.
Example 3
Multiply 795 × 531. Use the lattice multiplication method to show the answer.
Solution
Since we are multiplying a 3-digit number by a 3-digit number, we will use a 3 × 3 lattice grid.
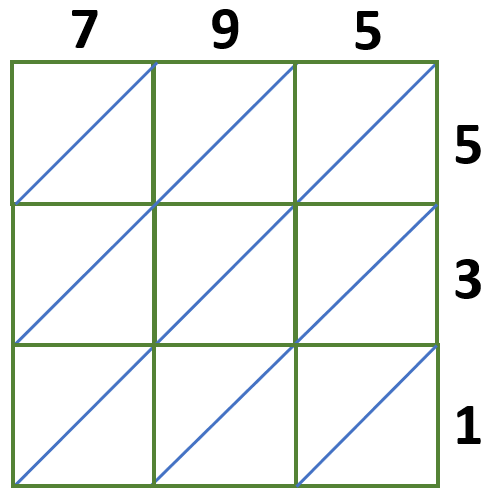
Multiply each digit and write these answers in the corresponding boxes we have,
7 × 5 = 35
9 × 5 = 45
5 × 5 = 25
7 × 3 = 21
9 × 3 = 27
5 × 3 = 15
7 × 1 = 07
9 × 1 = 09
5 × 1 = 05
The tens digits are written at the top left of the diagonal, while the ones digits are written at the bottom right of each box, as shown below.

Let us now get the sum of the number in each diagonal starting from the lower right corner of the lattice grid.
As shown below, we have the sums 14, 21, 12, and 12, the tens digits, which must be carried over to the next diagonal.
5 = 5
9 + 0 + 5 = 14
7 + 0 + 7 + 1 + 5 + 1 = 21
0 + 1 + 2 + 5 + 2 + 2 = 12
2 + 5 + 4 + 1 = 12
3 + 1 = 4
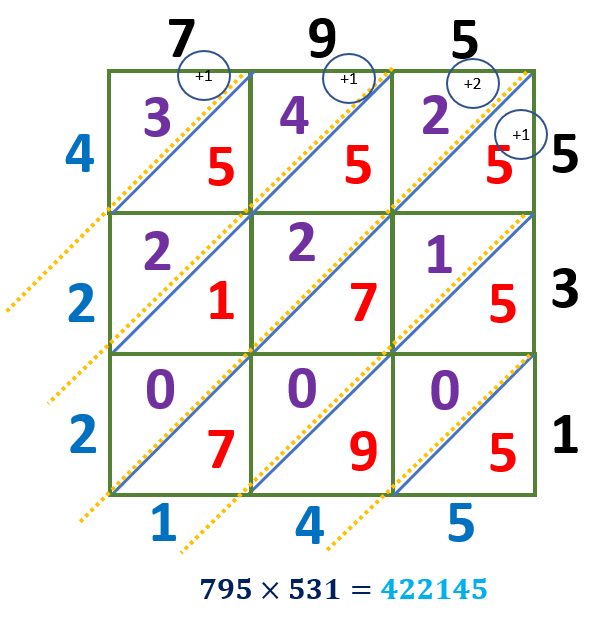
Write the product starting from the number at the top left and ending with the bottom right number. Thus, the product of 795 and 531 is equal to 422145.
Summary
Lattice multiplication is used as an alternative method to long multiplication or the grid method.
When using the lattice method of multiplication, we multiply each number’s digits and enter the result in the corresponding box. To create the digits of our answer, add the diagonals together.
Steps to the Lattice Multiplication Method
The lattice multiplication method involves the following steps:
Step 1: Draw the lattice grid that matches the number of digits.
Step 2: Label the lattice grid by taking the first number on top and the second number on the right of the lattice.
Step 3: Draw diagonal lines in each box. The lines must run from the bottom left corner of the boxes to the top right corner.
Step 4: Multiply each digit of the two numbers and write these answers in the corresponding boxes. The units are placed to the bottom right of the diagonal, while the tens are to the top left.
Step 5: Add up the numbers in each diagonal by starting at the right-hand side of the lattice grid. If the sum exceeds 9, carry over the tens digit to the next diagonal.
Step 6: Write the product starting from the number at the top left and ending with the bottom right number.
Frequently Asked Questions on Lattice Multiplication Method ( FAQs )
What is meant by the lattice multiplication method?
Lattice multiplication is used as an alternative method to long multiplication or the grid method. Lattice multiplication is frequently used in multiplying larger numbers.
When using the lattice method of multiplication, we multiply each number’s digits and enter the result in the corresponding box. To create the digits of our answer, add the diagonals together.
How do you draw a lattice multiplication grid?
The lattice multiplication grid is drawn using vertical and horizontal lines, forming a grid of squares. The number of squares will depend on the digits of the numbers involved in the multiplication. If we are multiplying 2-digit by a 2-digit number, we must use a 2 × 2 lattice grid, but if we are multiplying 3-digit by a 3-digit number, we must use a 3 × 3 lattice grid.
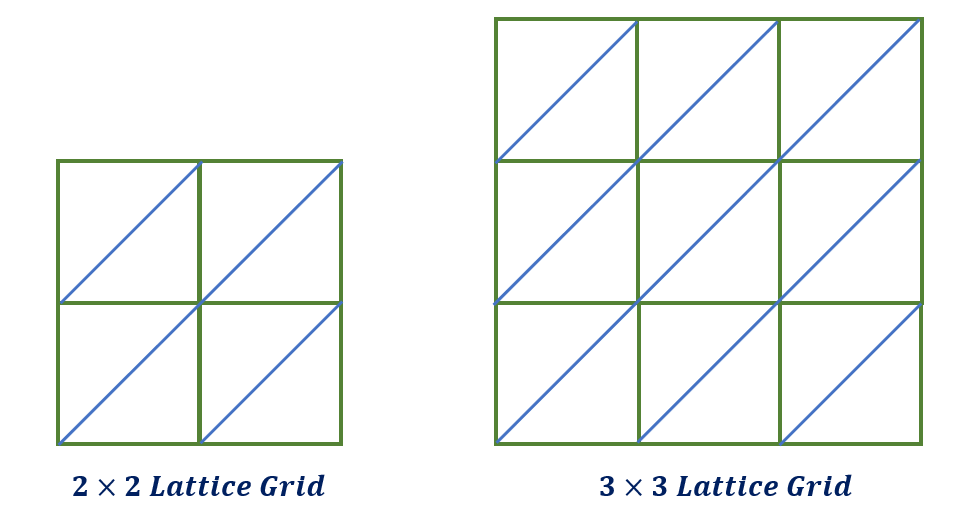
Diagonal lines are used to cut each square in half where the product of the digits is written. The units are placed to the bottom right of the diagonal, while the tens are to the top left.
Where is the lattice multiplication method used?
A method for multiplying numbers is called lattice multiplication, also referred to as Chinese multiplication. It is typically utilized when solving problems, including multiplying 2-digit by 2-digit numbers. However, it can also be applied when handling bigger multi-digit values.
Students learn how to multiply two larger numbers using this method, but they can also practice organizing their ideas and determining the place value of a given number. The lattice multiplication method is also a helpful way to multiply since it gives students a model to use to check that the numbers are correctly aligned.
Recommended Worksheets
Multiplication Tables (St. Patrick’s Day Themed) Math Worksheets
Multiplication Property (Valentine’s Day Themed) Math Worksheets
Multiplication Tables (St. Patrick’s Day Themed) Math Worksheets









