Area Method For Multiplication

Definition – Area method of multiplication

The area method, also sometimes called the box method, is an alternative to the standard algorithmic method for long multiplication. Both these methods use the distributive law for multiplication but they differ in how the partial products are calculated and written. It is important to note here that –

The area model is also known as the box model.
The area model of solving multiplication problems is derived from the concept of finding the area of a rectangle. Area of a rectangle = Length × Width.

What is multiplication?

The process of finding out the product between two or more numbers is called multiplication. The result thus obtained is called the product. Suppose, you bought 6 pens on one day and 6 pens on the next day. Total pens you bought are now 2 times 6 or 6 + 6 = 12.

This can also be written as 2 x 6 = 12

Note the symbol used for multiplication. The symbol (x) is generally used to represent multiplication. Other common symbols that are used for multiplication are the asterisk (*) and dot (.)

Some important terms used in multiplication are –

Multiplicand – The number to be multiplied is called the multiplicand.

Multiplier – The number with which we multiply is called the multiplier.

Product – The result obtained after multiplying the multiplier and the multiplicand is called the product.

The relation between the multiplier, multiplicand and the product can be expressed as –

Multiplier × Multiplicand = Product

Let us understand this using an example.

Suppose we have two numbers 9 and 5. We wish to multiply 9 by 5.

So, we express it as 9 x 5 which gives us 45.

Therefore, 9 x 5 = 45

Here, 9 is the multiplicand, 5 is the multiplier and 45 is the product.

How to multiply numbers using area method?

The following steps are following performing multiplication of numbers using area method –

Write the multiplicands in expanded form as hundreds, tens and ones etc.
Draw a 2 × 2 or 3 x 3 grid, that is, a box with the same number of rows and columns.
Write the terms of one of the multiplicands on the top of the grid (box), one on the top of each cell.
On the left of the grid, write the terms of the other multiplicand, one on the side of each cell.
Write the product of the number on the tens in the first cell. Then write the product of the tens and ones in the second and third cells. Write the product of the ones in the fourth cell.
In the last step, add all the partial products to get the final product.

Let us understand it using an example.

Suppose we wish to multiply 27 by 35. Let us perform this multiplication using the above stated steps.

The first step would be to write the multiplicands in expanded form as hundreds, tens and ones etc. we will have,

27 x 35 = ( 20 + 7 ) + ( 30 + 5 )

Now, we will place thee values in a 2 x 2 grid as shown below –

Now, we will write the product of the number on the tens in the first cell. Then we will write the product of the tens and ones in the second and third cells. Last, we will write the product of the ones in the fourth cell.

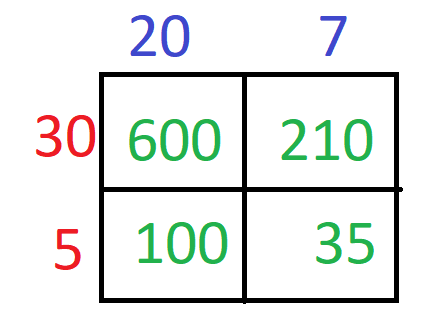
The last step is to add all the partial products to get the final product. So, we will have, 600 + 210 + 100 + 35 = 945

Hence, 27 x 35 = 945

How to multiply numbers using the standard method?

The following are the steps involved when multiplying numbers using the standard method.

First, we write the multiplicand and the multiplier in columns.
First, multiply the number at the one’s place of the multiplier with all the numbers of the multiplicand and write them horizontally.
Make sure you write numbers from right to left and each number below the corresponding place value of the multiplicand.
Now, move to the next line.
Place a 0 at the one’s place of this line.
Now, look for the digit at the ten’s place of the multiplier. Multiply the number at the ten’s place of the multiplier with all the numbers of the multiplicand and write them horizontally in the line where you had marked 0.
Again move to the next line.
Place a 0 at the one’s as well as ten’s place of this line.
Now, look for the digit at the hundred’s place of the multiplier. Multiply the number at the hundred’s place of the multiplier with all the numbers of the multiplicand and write them horizontally in the line where you had marked the two zeros.
Continue in this manner by adding an extra zero in each line until you have reached the end of the multiplier
Add the numbers vertically according to their place values.
The number so obtained is your result.

Let us understand it using an example.

For example, Multiply 341 by 120

Solution

We will use the following steps to obtain our result.

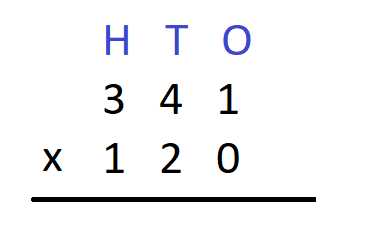
Step 1 – First we write the multiplicand and the multiplier in columns. Here we have 341 as the multiplicand and 120 as the multiplier.

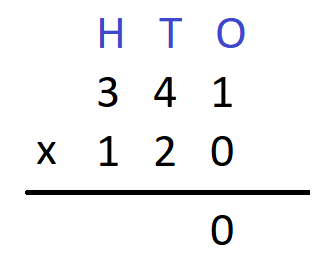
Step 2 – Now, we multiply the number at the one’s place of the multiplicand, i.e. 1 by the number at the one’s place of the multiplier, which in this case is 0. We get

Step 3 – Similarly, we multiply the number at the hundred’s place and the ten’s place of the multiplicand by 0. We get

Step 4 – Now, we need to place 0 at the ones’ place in the next line as a placeholder. We will get

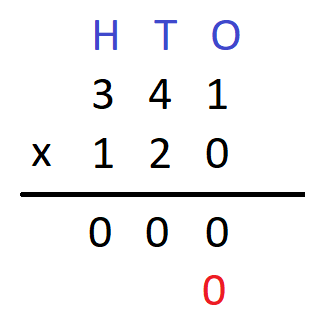
Step 5 Since, we are complete with the multiplication of the multiplicand with the first digit of the multiplier, we perform the same steps as above for the multiplication of the multiplicand with the next number of the multiplier and then write the result in the line against the 0 that we placed as a placeholder in the previous step. We will get –

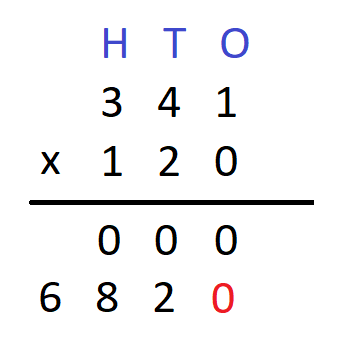
Step 6 – We will now repeat the steps 4 and 5 above to multiply the digit at the hundred’s place of the multiplicand with the corresponding digit of the multiplier. We will get –

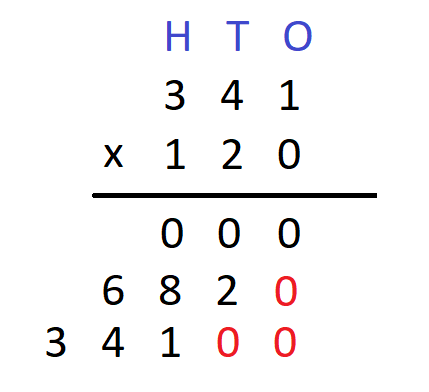
Step 7 Now that we have multiplied all the digits of the multiplier with the multiplicand, we will add the digits obtained in a vertical manner. We will get

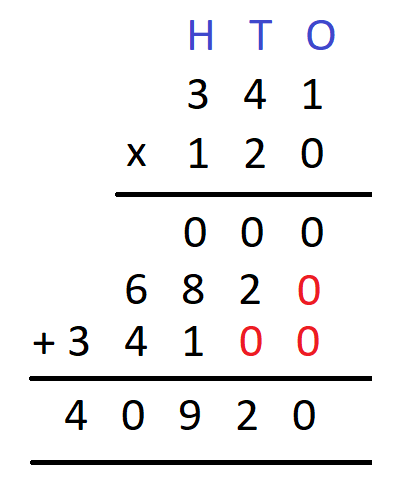
Hence, 341 x 120 = 40920

Comparison between standard method and area method of multiplication

The standard algorithm is generally a faster method but, unlike the area method, it does not promote understanding or encourage the development of mathematical thinking. It may be best to introduce your children to long multiplication with the area method before using the standard algorithm. The area method also supports the important ability to estimate answers. Let us compare both the methods with some examples.

Multiplication of a one digit number with a two digit number

Let us take an example where we want to multiply 5 by 24. How would we perform this multiplication by the standard method?

Multiplication by standard method

The following steps will be involved in multiplying 5 by 24 –

First, we write the multiplicand and the multiplier in columns. Recall that The number to be multiplied is called the multiplicand. The number with which we multiply is called the multiplier. The result obtained after multiplying the multiplier and the multiplicand is called the product. The relation between the multiplier, multiplicand and the product can be expressed as Multiplier × Multiplicand = Product. We will have,

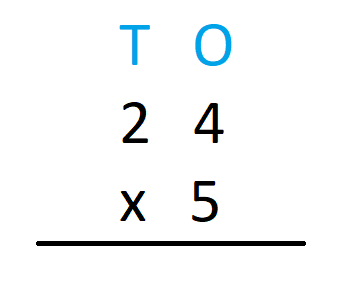
Multiply the one’s digit of the multiplicand by 5. We have 4 x 5 = 20. Write 0 in the one’s column and carry over 2 to the ten’s column.

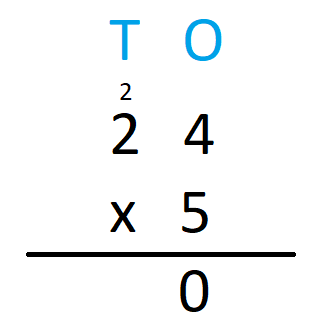
Multiply ten’s digit of the multiplicand by 5. We get 2 x 5 = 10. Add 2 that was carried over to it to get 10 + 2 = 12 Now, write 2 in the ten’s column and 1 in the hundred’s column. We will have,

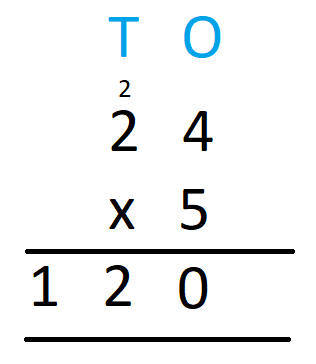
Hence, we have 24 x 5 = 120

Now, let us perform the same multiplication using the area method.

Multiplication by area method

The following steps will be involved in multiplying 5 by 24 –

The first step would be to write the multiplicands in expanded form as hundreds, tens and ones etc. we will have,

24 x 5 = ( 20 + 4 ) x 5

Now, we will place thee values in a 1 x 2 grid as shown below –

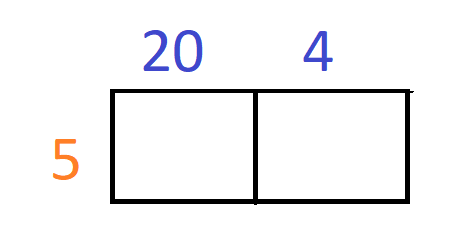
Now, we will write the product of the number on the tens in the first cell. Then we will write the product of ones in the second cell.

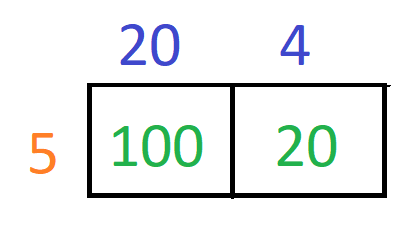
The last step is to add all the partial products to get the final product. So, we will have, 100 + 20 = 120

Hence, 24 x 5 = 120

We can see that irrespective of the method used, we shall get the same result.

Multiplication of a two digit number with a two digit number

Let us take an example where we want to multiply 25 by 34. How would we perform this multiplication by the standard method?

Multiplication by standard method

The following steps will be involved in multiplying 25 by 34 –
We will use the following steps to obtain our result.

Step 1 – First we write the multiplicand and the multiplier in columns.

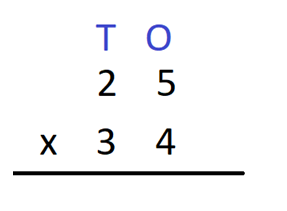
Step 2- Multiply the one’s digit of the multiplicand by 4. We have 4 x 5 = 20. Write 0 in the one’s column and carry over 2 to the ten’s column.

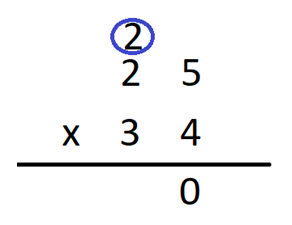
Step 3 – Multiply ten’s digit of the multiplicand by 4. We get 2 x 4 = 8. Add 2 that was carried over to it to get 8 + 2 = 10 Now, write 0 in the ten’s column and carry over 1 to the hundred’s column.

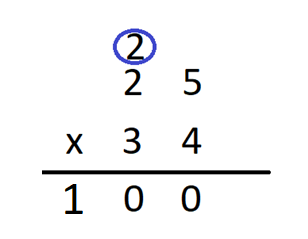
Step 4 Now, we need to place 0 at the ones’ place in the next line as a placeholder. We will get

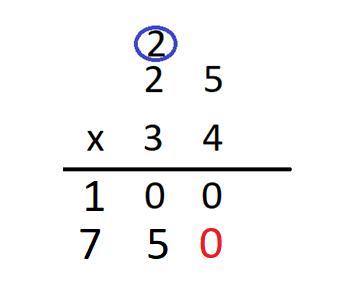
Step 6 Now that we have multiplied all the digits of the multiplier with the multiplicand, we will add the digits obtained in a vertical manner. We will get

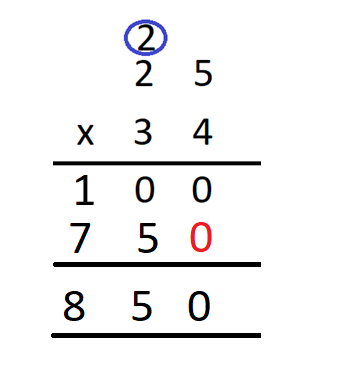
The result thus obtained is our answer. Hence 25 x 34 = 850

Multiplication by area method

The following steps will be involved in multiplying 25 by 34 –

The first step would be to write the multiplicands in expanded form as hundreds, tens and ones etc. we will have,

25 x 34 = ( 20 + 5 ) x ( 30 + 4 )

Now, we will place thee values in a 2 x 2 grid as shown below –

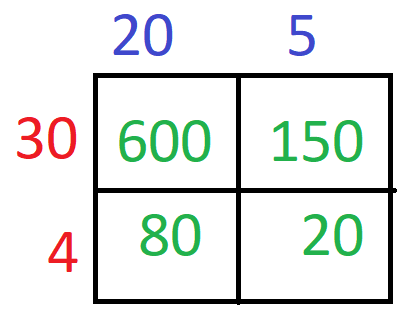
The last step is to add all the partial products to get the final product. So, we will have, 600 + 150 + 80 + 20 = 850

Hence, 25 x 34 = 850

We can see that irrespective of the method used, we shall get the same result.

Multiplication of a three digit number with a three digit number

Let us take an example where we want to multiply 304 by 125. How would we perform this multiplication by the standard method?

Multiplication by standard method

The following steps will be involved in multiplying 304 by 125 –
We will use the following steps to obtain our result.

We will use the following steps to obtain our result.

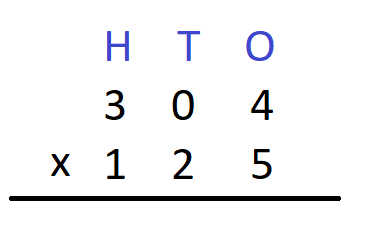
Step 1 – First we write the multiplicand and the multiplier in columns. Here, the multiplicand is 304 and the multipliers is 125

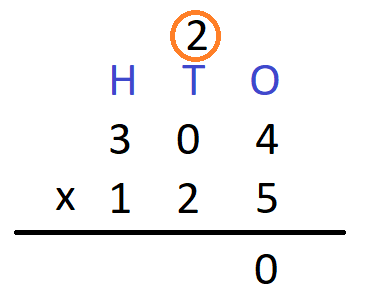
Step 2- Multiply the one’s digit of the multiplicand by 5. We have 4 x 5 = 20. Write 0 in the one’s column and carry over 2 to the ten’s column.

Step 3 – Multiply ten’s digit of the multiplicand by 5. We get 5 x 0 = 0. Add 2 that was carried over to it to get 0 + 2 = 2 Now, write 2 in the ten’s column to get

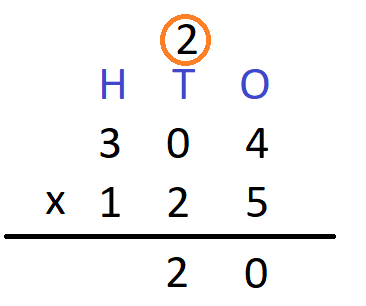
Step 4 – Multiply the hundred’s digit of the multiplicand by 5. We get 3 x 5 = 15. Now, write 5 in the hundred’s column and 1 in the ten thousand’s column.

Step 5 Now, we need to place 0 at the ones’ place in the next line as a placeholder. We will get

Step 6 – Next, we repeat the above steps to multiply all digits of the multiplicand by the digit at the ten’s place of the multiplier. We will get

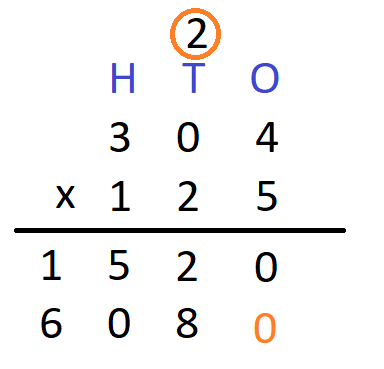
Step 7 Now, we need to place 0 at the ones’ and the ten’s place in the next line as a placeholder. We will get

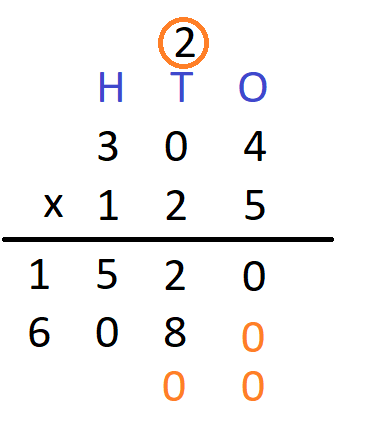
Step 8 – Again, we repeat the above steps to multiply all digits of the multiplicand by the digit at the hundred’s place of the multiplier. We will get

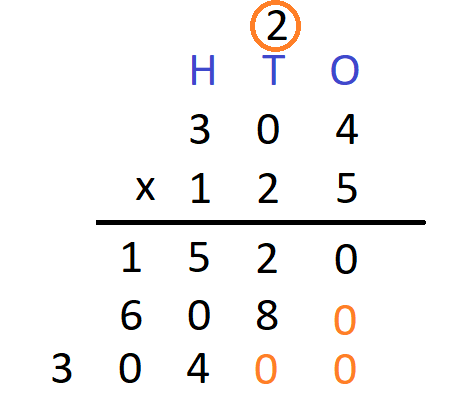
Step 9 Now that we have multiplied all the digits of the multiplier with the multiplicand, we will add the digits obtained in a vertical manner. We will get

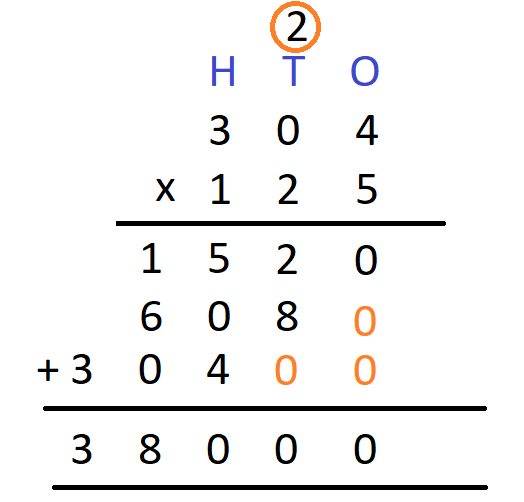
Hence, 304 x 125 = 38000

Multiplication by area method

The following steps will be involved in multiplying 304 by 125 –

The first step would be to write the multiplicands in expanded form as hundreds, tens and ones etc. we will have,

304 x 125 = ( 300 + 0 + 4 ) x ( 100 + 20 + 5 )

Now, we will place thee values in a 3 x 3 grid as shown below –

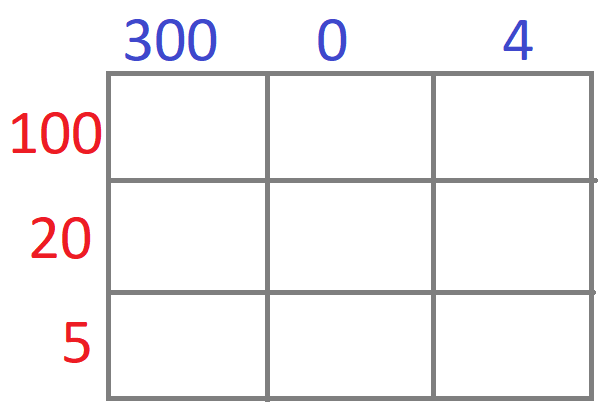
Now, we will write the product of the number on the hundreds in the first cell. Then we will write the product of the tens and ones in the second and third cells. Similarly, we will multiply and write the values in the remaining cells. We will have,

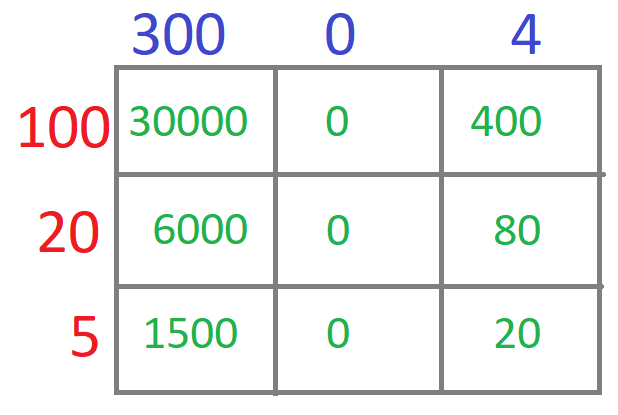
The last step is to add all the partial products to get the final product. So, we will have, 30000 + 0 + 400 + 6000 + 0 + 80 + 1500 + 0 + 20 = 38000

Hence, 304 x 125 = 38000

We can see that irrespective of the method used, we shall get the same result.

Key Facts and Summary

The area method, is an alternative to the standard algorithmic method for long multiplication.
The number with which we multiply is called the multiplier. The result obtained after multiplying the multiplier and the multiplicand is called the product. The relation between the multiplier, multiplicand and the product can be expressed as Multiplier × Multiplicand = Product.
The area model is also known as the box model.
The area model of solving multiplication problems is derived from the concept of finding the area of a rectangle.
Area of a rectangle = Length × Width.

Recommended Worksheets

Multiplication Property (Valentine’s Day Themed) Math Worksheets
Multiplication Tables (St. Patrick’s Day Themed) Math Worksheets
Fact Families for Multiplication and Division (Summer Themed) Math Worksheets

Browse All Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We appreciate your support!