What is addition?
Addition, in mathematics, can be defined as the process of combining two or more numbers together to make a new total or sum. The numbers to be added together are called addends and the result thus obtained is called the sum.
What is subtraction?
The process of finding the difference between two numbers is known as subtraction. In other words, it is the process of taking away a number from another. The number that is subtracted is called the subtrahend while the number from which the subtrahend is subtracted is called minuend. The result of this subtraction is called the difference.
Importance of place value in addition and subtraction
Place value has an important role to play in defining the algorithm for addition as well as subtraction. We know that the place value is the basis of our entire number system. This is the system in which the position of a digit in a number determines its value. The place value of a digit in a number is the value it holds to be at the place in the number. Therefore, the number 65,471 is different from 17,645 because the digits are in different positions.
In the place value system, the numbers are written by using the digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 with each symbol getting a value depending on the place it occupies in the place value chart. For example, three million two hundred seventy eight thousand nine hundred forty-seven represents a collection of 3 million, 278 thousand, 9 hundred, 4 tens and 7 units. Therefore, it is written by putting 3 in the millions place, 2 in hundreds thousand’s place, seven in ten thousand places, 8 in the thousands place, 9 in the hundreds place, 4 in ten’s place and 7 in the units place. We use the base ten number system to write numbers with each place having a value; ones, tens, hundreds, thousands, and so on.
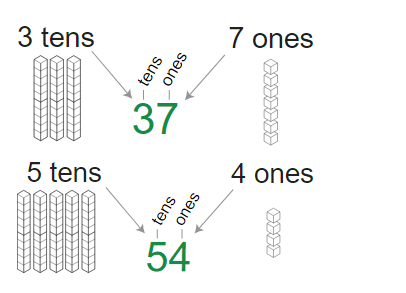
Algorithms for the addition of two numbers
For the addition of numbers, each number I arranged according to its place value. There may be different conditions, whether we need to carry forward a digit to the next place value or not. Let us discuss these conditions.
Addition with No Carrying Forward
For adding a Single Digit with a Two-Digit Number, the digit at the one’s place value of the first number will be added to the digit at the one’s place of the second number.
Let us understand it using an example.
Suppose we want to add 5 and 13.
5 – 5 is at the unit’s place in the number.
13 – 1 is the ten’s place while 3 is the unit’s place.
So, we add the unit’s digit of both the number as shown below –
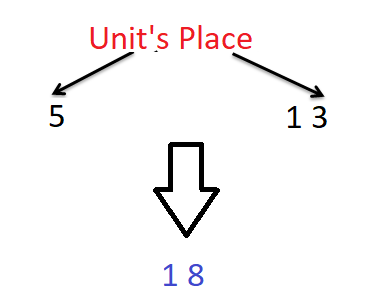
Here we can see that 5 + 3 = 8 < 10, so the result obtained was a single digit number at the unit’s place. But if we were to add the numbers 5 + 16, we would have got 5 + 6 = 11, then how would we have written 11 in the answer. This is where the concept of carrying forward comes into force.
Let us consider another example.
Example
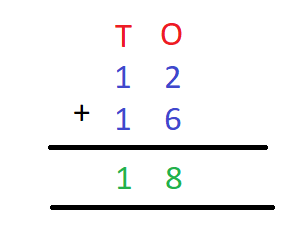
Consider two numbers 12 and 16. Suppose we want to add these two numbers. How will we find their sum? Let us find out.
Solution
Recall that,
12 = 1 tens + 2 ones
16 = 1 tens + 6 ones
Therefore,
The sum of 12 and 16 will be given by adding the respective one’s digits with each other and the ten’s digits with each other. We will have,
12 +16 = = 1 tens + 2 ones
+ 1 tens + 6 ones
2 tens + 8 ones
Hence, 12 + 16 = 28
Addition with Carrying forward
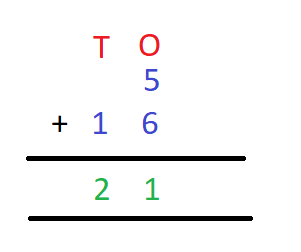
Let us consider two numbers 5 and 16. How will we add these two numbers? Let us find out.
5 = 0 tens + 5 ones
16 = 1 tens + 6 ones.
Therefore,
5 + 16 = 0 tens + 5 ones
+ 1 tens + 6 ones
1 tens + 11 ones
Now, 11 ones = 1 tens + 1 ones
Therefore, we have 5 + 16 = 1 tens +1 tens + 1 ones = 2 tens + 1 ones.
Hence, 5 + 16 = 21
Let us consider another example
Example
Let us consider two numbers 28 and 16. How will we add these two numbers? Let us find out.
Solution
We will follow the following steps to add these numbers.
- We know that 28 = 2 tens + 8 ones and 16 = 1 tens + 6 ones
- Now, 8 ones + 6 ones = 14 ones. As the sum of the digits at the one’s place exceeds 9, you must carry ones into tens.
- 14 ones = 10 ones + 4 ones = 1 tens + 4 ones
- Write 4 under ones column and carry
- Add the tens
- 1 ten ( that was carried over ) + 2 tens + 1 ten = 4 tens.
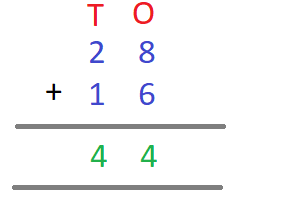
- Thus 28 + 16 = 44
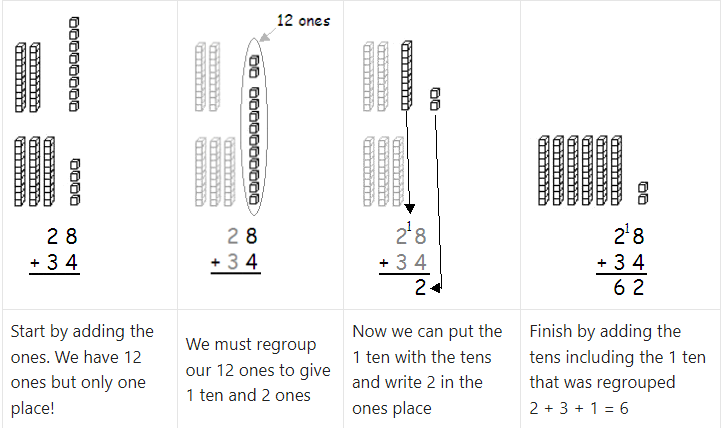
Graphical representation of addition with grouping
Let us understand the graphical representation of the addition of two numbers through an example.
Suppose we want to add 28 and 34. How will we represent this addition? Below is the graphical representation of this addition.
Algorithms for subtraction between two numbers
There may be different cases when we subtract one number from another. These are –
- Subtraction without borrowing
- Subtract with borrowing
Let us discuss these one by one.
Subtraction of Two-Digit Numbers (Without borrowing)
When we subtract one two-digit number from another, we may have the following conditions –
Case 1 – Both the subtrahend and the minuend are two-digit numbers
When we subtract a one-digit number from another one-digit number, we directly subtract the subtrahend from the minuend and get the result.
But, in two digits numbers, we have digits at two places, tens and ones. So, in order to subtract one two-digit number from another, we place the subtrahend below the minuend in the order of their place values and subtract accordingly.
The following are the steps involved in subtraction –
1. Place the values vertically in order of their place values.
2. Start subtracting the numbers, starting from the one’s place.
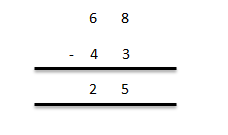
For example, let us subtract 43 from 68. Both are two-digit numbers, therefore placing one number below the other in order of their place values, we get –
Case 2 – The minuend is a two-digit number while the subtrahend is a one-digit number
If a minuend is a two-digit number and the subtrahend is a one-digit number, we place one number below the other in order of their place values.
For example, let us subtract 5 from 79. Here the minuend, 79 is a two-digit number while the subtrahend, 5 is a one-digit number. So, in order to subtract a one-digit number from a two-digit number, we place the subtrahend below the minuend in the order of their place values and subtract accordingly.
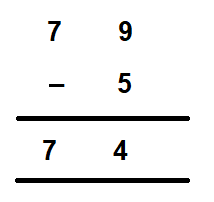
Subtraction of Three-Digit Numbers (Without borrowing)
When we subtract one three digit number from another, we may have the following conditions –
Case 1 – Both the subtrahend and the minuend are three-digit numbers
Subtraction of three-digit numbers is in a way similar to that of the two-digit numbers. In three digits numbers, we have digits at three places, hundreds, tens, and ones. So, in order to subtract one three-digit number from another, we place the subtrahend below the minuend in the order of their place values and subtract accordingly.
For example, let us subtract 123 from 658. Both are three-digit numbers, therefore placing one number below the other in order of their place values, we get –
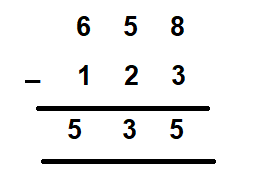
Case 2 – The Minuend is a three-digit number while the subtrahend is either a one-digit number or a two-digit number
If the minuend is a three-digit number and the subtrahend is either a one-digit number or a two-digit number, we place one number below the other in order of their place values.
For example, let us subtract 21 from 794. Here the minuend, 794 is a three-digit number while the subtrahend, 21 is a two-digit number. So, in order to subtract a two-digit number from a three-digit number, we place the subtrahend below the minuend in the order of their place values and subtract accordingly.
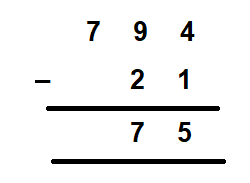
Let us now subtract 4 from 237. Here the minuend, 237 is a three-digit number while the subtrahend, 4 is a one-digit number. So, in order to subtract a one-digit number from a three-digit number, we place the subtrahend below the minuend in the order of their place values and subtract accordingly.
Subtraction of Numbers (With Borrowing)
Until now, we have discussed problems of subtractions where each digit of the subtrahend was less than the corresponding digit in the minuend. How would we subtract a subtrahend that is greater at a certain place value than the corresponding value of the minuend?
Let us understand this by an example. Suppose, we wish to subtract 2356 from 7814. Compare the corresponding digits of both the subtrahend and the minuend. You will notice that the value of subtrahend is larger than the value of the minuend at some places. So, how do we subtract 4 from 6? This is where borrowing comes into the picture. In such cases, we borrow 1 from the next number in the place value.
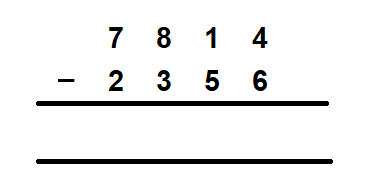
Let us solve this step by step.
- Subtract 6 from 4. We cannot larger numbers, so we borrow 1 from the digit that is at the ten’s place in the minuend. In this case, the number is 1. So we borrow 1 from 1, and the 1 at the ten’s place in the minuend becomes 0. But the number at the one’s place of the minuend, after borrowing 1 becomes 14. Now we can subtract 6 from 14 and we get 8 at the one’s place as the answer.
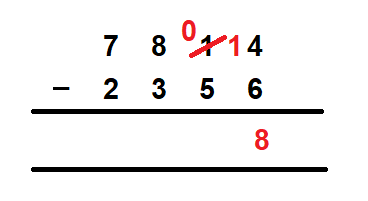
- Next, we move to subtract the digits at the ten’s place. Remember, the digit at the ten’s place is now 0, instead of the 1 that we had earlier. So, we need to subtract 5 from 0, which again is not possible. Therefore, we repeat the steps again that we did for subtracting the digits at the one’s place. We will borrow 1 from the digit at the hundred’s place, and give it to 0 at the ten’s place. So, 8 at the hundred’s place of the minuend becomes 7 and the 0 at the ten’s place of the minuend becomes 10. Now we can subtract 5 from 10 and we get 5 as the answer at the ten’s place.
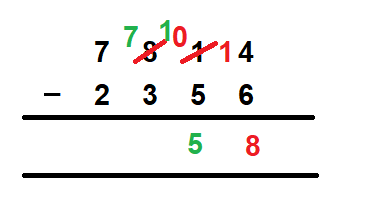
- Next, we look at the values at the hundred’s place. Here, we have 3 as the subtrahend and 7 as the minuend which can be easily subtracted. So, we get 4 as the answer at the hundred’s place.
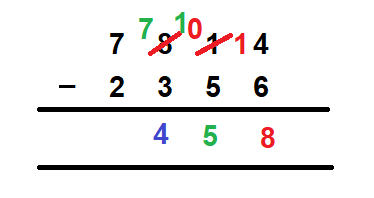
- Last, we check the values at the thousand’s place. We have 2 as the subtrahend and 7 as the minuend. Hence, we get 5 as the answer at the thousand’s place.
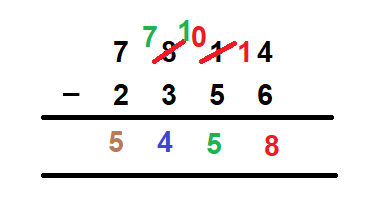
Hence, 7814 – 2356 = 5458
Addition and subtraction in Decimals
Can we use the same algorithms that we discussed above to add and subtract decimals? Let us find out.
Algorithm for the addition of decimals
Addition of decimals is as simple as the addition of whole numbers. The only difference is that we ensure the alignment of the decimal points of given numbers before their addition. The following steps are used to add numbers with decimals –
- Convert the given decimals to like decimals.
- Write the decimals in columns with the decimal points directly below each other so that tenths come under tenths, hundredths come under hundredths and so on.
- Add as we add whole numbers.
- Place the decimal point in the answer directly below the other decimal points.
Let us understand the above steps with an example.
Example
Suppose we want to add the decimal numbers 15.44, 7.524 and 25
Solution
We have been given the decimal numbers 15.44, 7.524 and 25
First of all, we will have to convert these decimals into like decimals. Therefore,
15.44 = 15.440
7.524 is already a like decimal so no conversion is required.
25 = 25.000
Now, that all the three decimals are like decimals, we will proceed ahead and write these decimals in column form, as shown below –
1 5 . 4 4 4
+ 7 . 5 2 4
+ 2 5 . 0 0 0
Next, we will add these fractions just as we add the whole numbers. We will get,
1 5 . 4 4 4
+ 7 . 5 2 4
+ 2 5 . 0 0 0
+ 4 7 . 9 6 4
Hence, the addition of 15.44, 7.524 and 25 is 47.964
Algorithm for subtraction in decimals
To subtract a decimal number from another decimal number, we follow the same procedure as we did in addition. The following steps for the subtraction of a decimal number from another decimal number –
- Convert the given decimals to like decimals.
- Write the decimals in columns with the decimal points directly below each other so that tenths come under tenths, hundredths come under hundredths and so on.
- Subtract as usual ignoring the decimal points.
- Place the decimal point in the answer directly below the other decimal points.
Let us understand the above steps with an example –
Example
Suppose we want to find the value of 11.6 – 9.847
Solution
We have been given the decimals, 11.6 and 9.847 and we are required to find their difference.
First of all, we will have to convert these decimals into like decimals. Therefore,
11.6 = 11.600
9.847 is already a like decimal so no conversion is required.
Next, we will subtract these fractions just as we add the whole numbers. We will get,
1 1 . 6 0 0
– 9 . 8 4 7
1. 7 5 3
Therefore, 11.6 – 9.847 = 1.753
Key Facts and Summary
- Addition, in mathematics, can be defined as the process of combining two or more numbers together to make a new total or sum.
- The numbers to be added together are called addends and the result thus obtained is called the sum.
- The process of finding the difference between two numbers is known as subtraction. In other words, it is the process of taking away a number from another.
- The number that is subtracted is called the subtrahend while the number from which the subtrahend is subtracted is called minuend. The result of this subtraction is called the difference.
- A single-digit has the place value of a unit in the place value system of the numbers.
- For adding a Single Digit with a Two-Digit Number, the digit at the one’s place value of the first number will be added to the digit at the one’s place of the second number.
- For adding two or more decimal numbers, write down the decimal numbers, one number under the other number and line up the decimal points. Convert the given decimals to like decimals. Arrange the addends in such a way that the digits of the same place are in the same column. Add the numbers from the right as we carry addition usually.
- For finding the difference between two or more decimal numbers, write down the decimal numbers, one number under the other number and line up the decimal points. Convert the given decimals to like decimals. Arrange the addends in such a way that the digits of the same place are in the same column. Subtract the numbers from the right as we carry addition usually.
Recommended Worksheets
Addition Property (Chinese New Year Themed) Math Worksheets
Place Value: Ten Thousand and Hundred Thousand (Chinese New Year Themed) Math Worksheets
Subtraction of 1- Digit Numbers (Family Fit Lifestyle Month Themed) Math Worksheets









