What are single-digit numbers?
Single-digit numbers are numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The smallest single-digit number is 0 and the largest single-digit number is 9. However, the smallest counting number is 1. The place value of a single-digit number is called the ones place or units digit.
Single-digit numbers can be expressed in different ways such as in numerical form, in words, by blocks, or by random objects.
| Numerical Form | Words | Blocks | Objects |
| 0 | zero | ||
| 1 | one |  | |
| 2 | two |   | |
| 3 | three |    | |
| 4 | four |     | |
| 5 | five |      | |
| 6 | six |       | |
| 7 | seven |        | |
| 8 | eight |         | |
| 9 | nine |          | |
| 10 | ten |           |
How to add single-digit numbers?
When adding single-digit numbers, we usually use the horizontal or vertical method and then add the terms. The addends are the numbers to which the addition process will be applied. The sum is the result of adding the addends. The plus sign is the symbol that denotes the addition process.
Horizontal Method
The horizontal method of adding single-digit numbers is the most common method in adding single-digit numbers without regrouping.
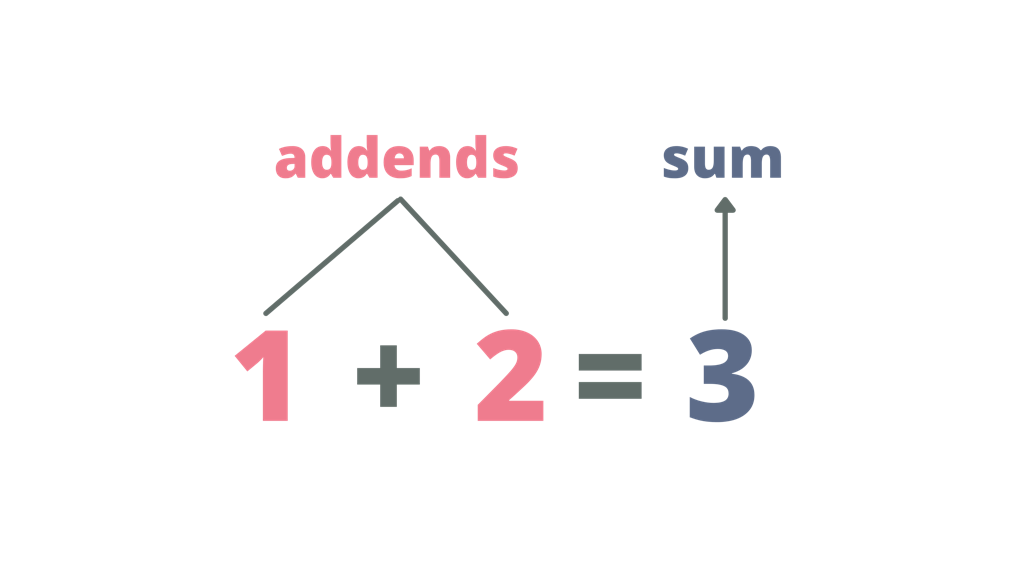
Vertical Method
The vertical method of addition is frequently used if it the addends are multi-digit numbers or if the addition process needs regrouping. Using the vertical approach is the easiest method of adding large numbers because we can align the place values accordingly.
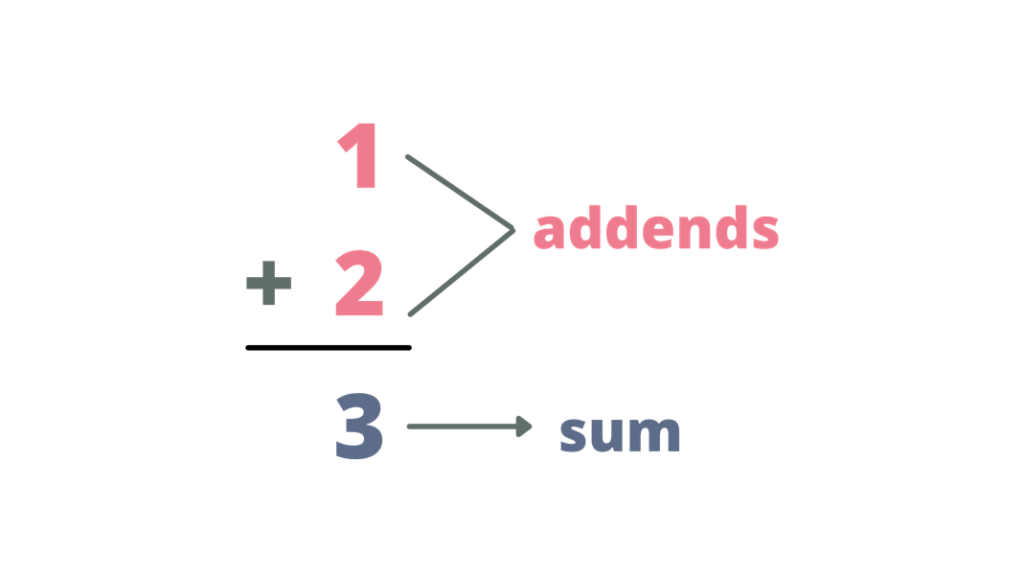
Adding single-digit numbers without regrouping
To add single-digit numbers, follow these steps:
- Write the numbers horizontally or vertically.
- Add the numbers in the units digit.
Example #1
What is the sum of 4 and 3?
Solution
| Addition Process | Step-by-Step Explanation |
| 4 + 3 = | Arrange the numbers horizontally and denote the addition process. |
| 4 + 3 = 7 | Adding 4 and 3 will result to 7. |
| Therefore, the sum of 4 and 3 is 7. |
Example #2
Find the sum of 5 and 4.
Solution
| Addition Process | Step-by-Step Explanation |
| 5 + 4 = | Denote the addition process by writing the numbers in a horizontal manner. |
| 5 + 4 = 9 | Adding 5 and 4 will result to 9. |
| Therefore, the sum of 5 and 4 is 9. |
Example #3
What is the result of 3 + 1?
Solution
| Addition Process | Step-by-Step Explanation |
| 3 + 1 = | Arrange the numbers horizontally and denote the addition process. |
| 3 + 1 = 4 | Adding 3 and 1 will result to 5. |
| Therefore, the result of adding 3 and 1 is 4. |
Example #4
What is the sum of 6 and 2?
Solution
| Addition Process | Step-by-Step Explanation |
| 6 + 2 = | Denote the addition process by writing the numbers in a horizontal manner. |
| 6 + 2 = 8 | Adding 6 and 2 will result to 8. |
| Therefore, the result of adding 6 and 2 is 8. |
Example #5
Determine the sum of 2 and 3.
Solution
| Addition Process | Step-by-Step Explanation |
| 2 + 3 = | Denote the addition process by writing the numbers in a horizontal manner. |
| 2 + 3 = 5 | Adding 2 and 3 will result to 5. |
| Therefore, the result of adding 2 and 3 is 5. |
Adding single-digit numbers with regrouping
To introduce the concept of adding single-digit numbers that need regrouping is to create a group of ten. Say, for example, we have 7 and 5 apples. How many apples do we have?
When represented in objects, we can easily count the number of apples that we have.

To make counting easier, we can transfer 3 apples from 5 apples to create a group of 10 apples. Thus,
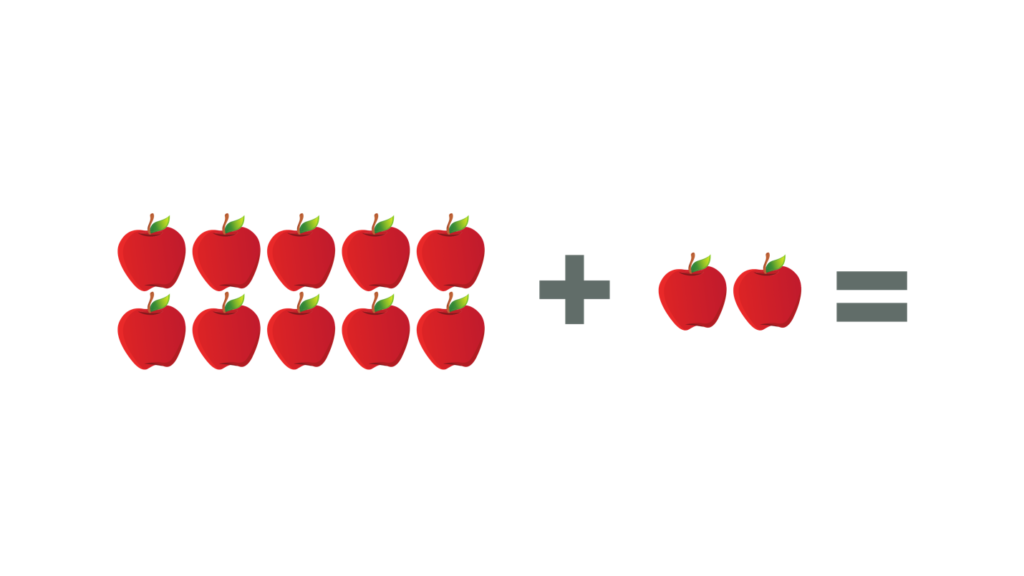
This way, just be looking, we can say that there are 12 apples.
When adding single-digit numbers with regrouping, we need to familiarize ourselves with the word carry over – or carry 1. A carry over is a single digit that is regrouped from one column of digits to the column of a higher place value – in this case, we will carry over 1 to the tens digit.
The figure below shows the placement of a carry over when adding single-digit numbers.
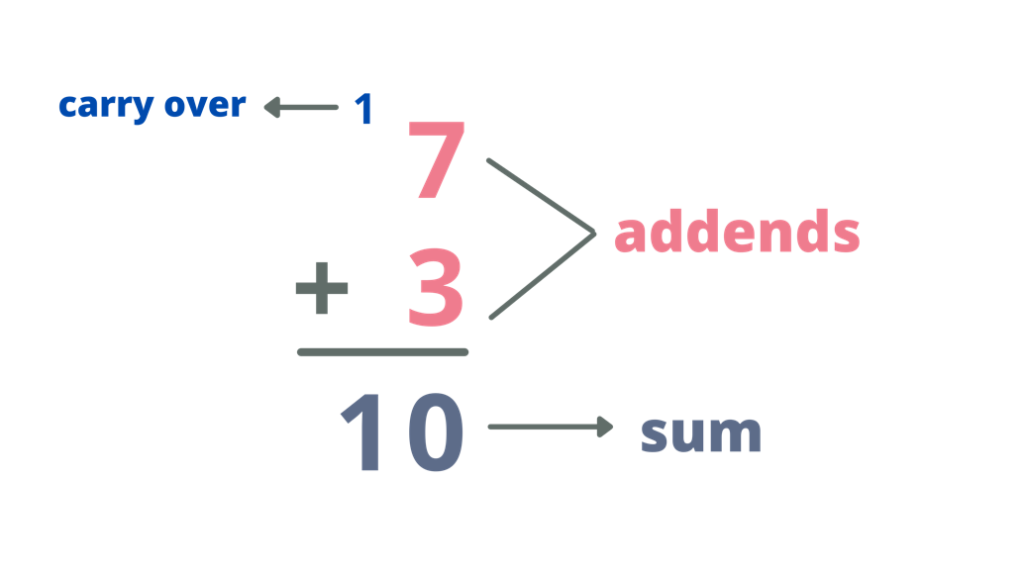
To add single-digit numbers that need regrouping, follow these steps:
- Write the numbers with the place values lines up.
- Add the digits in the ones place. If the sum exceeds 10, then carry over the digit to the tens place.
- Bring down the carry over on the column of the tens place.
Example #1
What is the sum of 6 and 8?
Solution
| Addition Process | Step-by-Step Explanation |
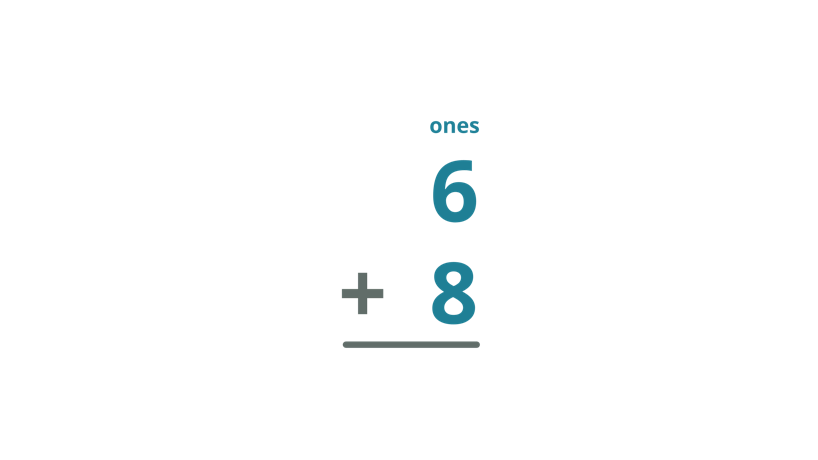 | Arrange the numbers in a column form with the place values lined up. |
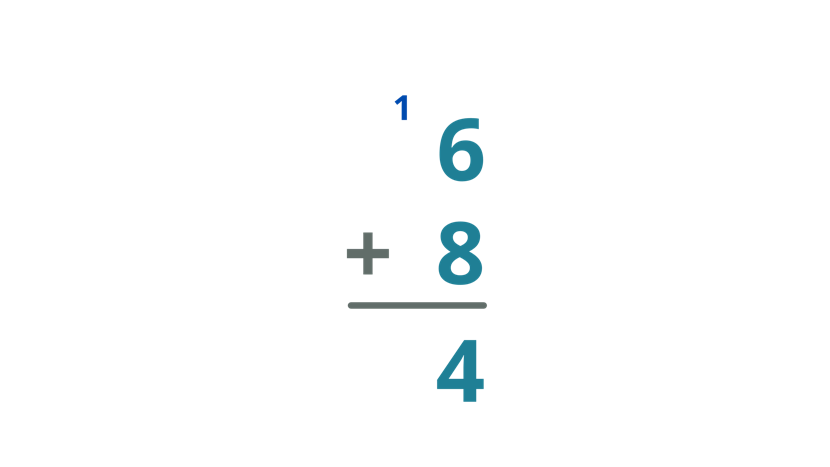 | Add the numbers in the column of the units digit. Thus,6 + 8 = 14 Since the sum of 6 and 8 is 14, write 4 below the bar and put the carry over on the tens column. |
 | Bring down the carry over and write it below the bar. |
| Therefore, the sum of 6 and 8 is 14. |
Example #2
Determine the sum of 3 and 9.
Solution
| Addition Process | Step-by-Step Explanation |
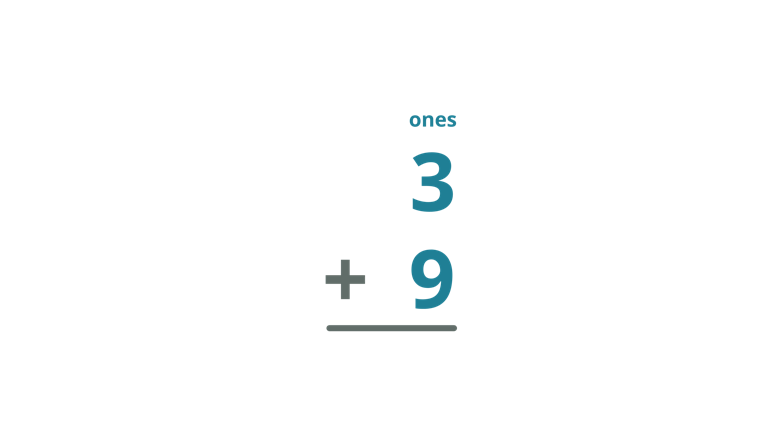 | Arrange the numbers in a column form with the place values lined up. |
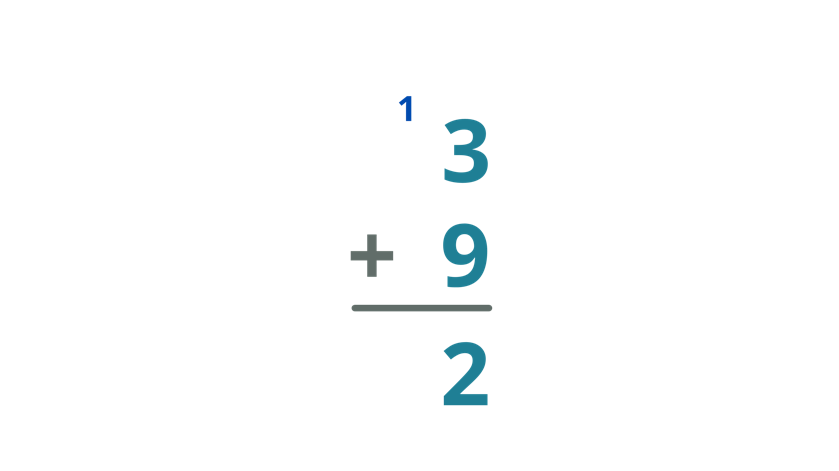 | Get the sum of 3 and 9. Thus,3 + 9 = 12 Since the sum of 3 and 9 is 12, write 2 below the bar and put the carry over on the tens column. |
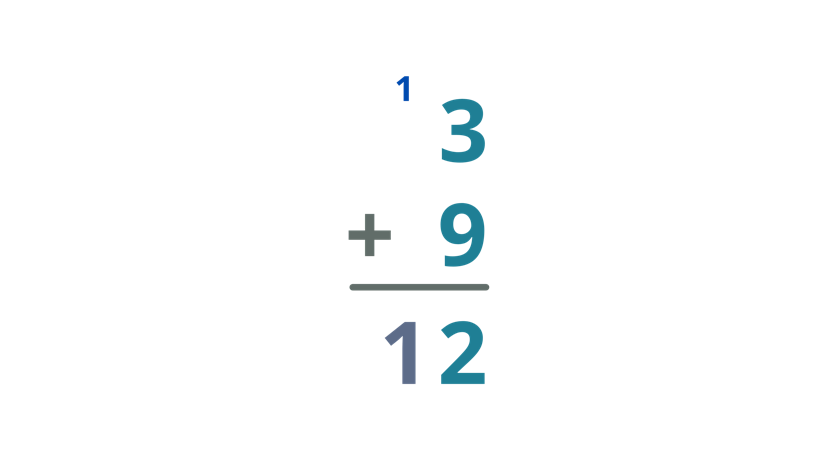 | Bring down the carry over and write it below the bar. |
| Therefore, the sum of 3 and 9 is 12. |
Example #3
Find the sum of 8 and 5.
Solution
| Addition Process | Step-by-Step Explanation |
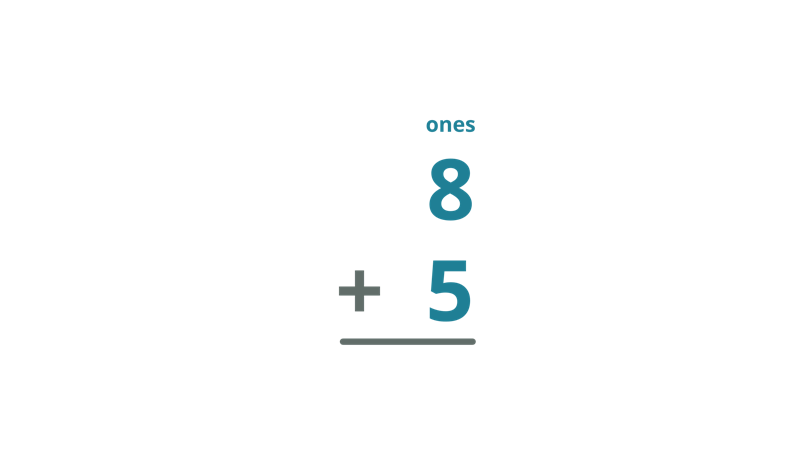 | Arrange the numbers in a column form with the place values lined up. |
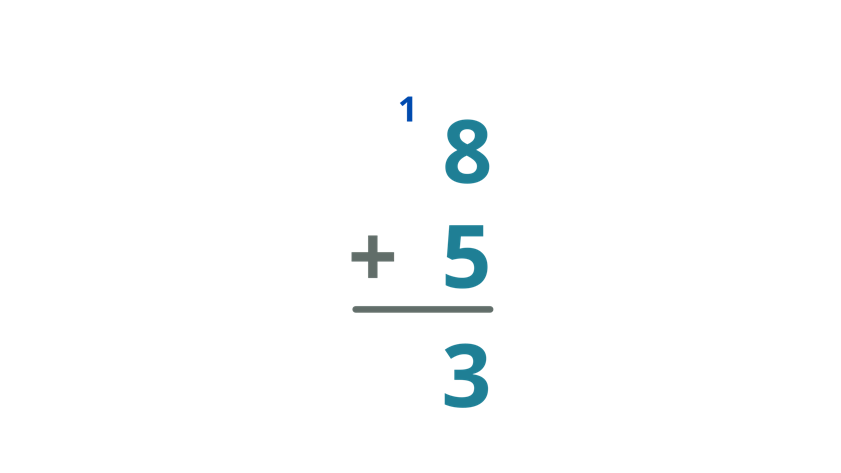 | Add the numbers in the column of the units digit. Thus,8 + 5 = 13 Since the sum of 8 and 5 is 13, write 3 below the bar and put the carry over on the tens column. |
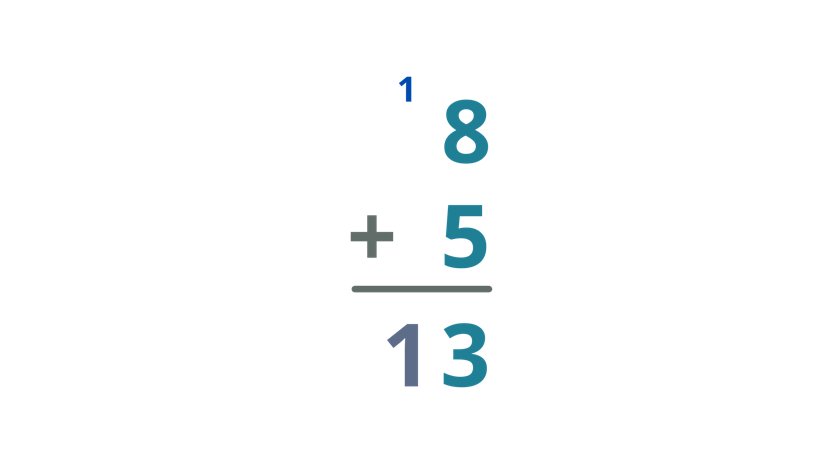 | Bring down the carry over and write it below the bar. |
| Therefore, the sum of 8 and 5 is 13. |
Example #4
What is the sum of 4 and 7?
Solution
| Addition Process | Step-by-Step Explanation |
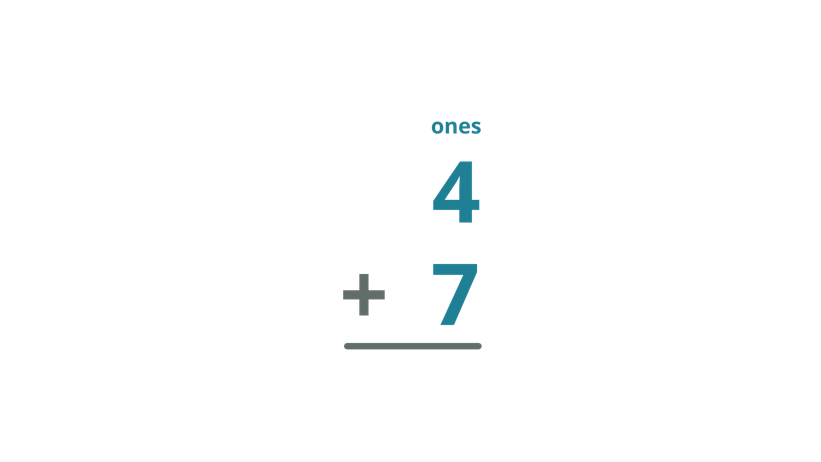 | Arrange the numbers in a column form with the place values lined up. |
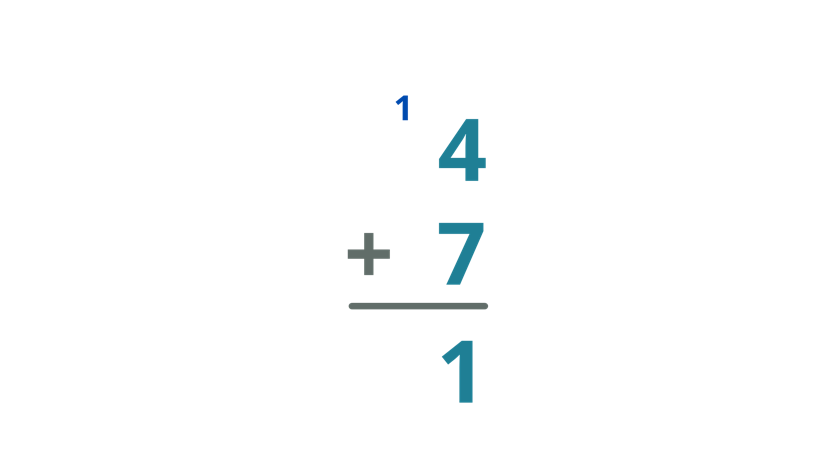 | Get the sum of 4 and 7. Thus,4+ 7 = 11 Since the sum of 4 and 7 is 11, write 1 below the bar and put the carry over on the tens column. |
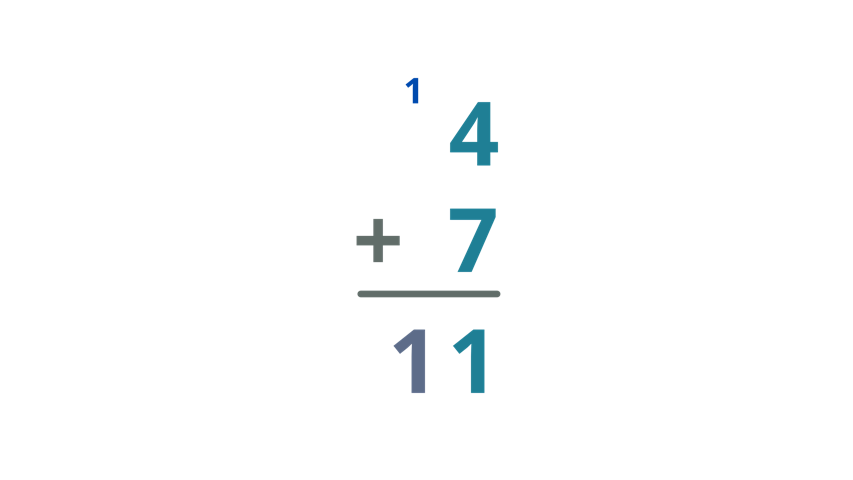 | Bring down the carry over and write it below the bar. |
| Therefore, the sum of 4 and 7 is 11. |
Example #5
What is the sum of 4 and 7?
Solution
| Addition Process | Step-by-Step Explanation |
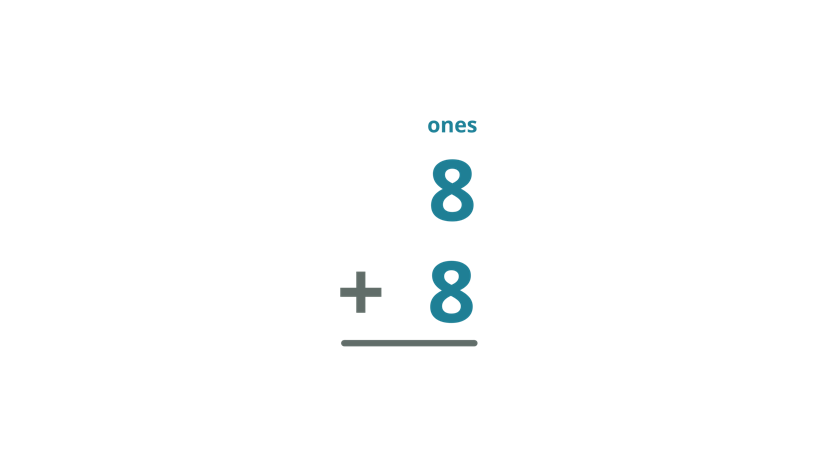 | Arrange the numbers in a column form with the place values lined up. |
 | Add the numbers in the column of the units digit. Thus, 8 + 8 = 18 Since the sum of 8 and 8 is 18, write 8 below the bar and put the carry over on the tens column. |
 | Bring down the carry over and write it below the bar. |
| Therefore, the sum of 8 and 8 is 16. |
How to subtract single-digit numbers?
To subtract is to take something away from a group or a collection of things. When we remove items from a certain group, the group’s total number decreases or becomes smaller. When we subtract two numbers, we use the terms minuend, subtrahend, minus sign, and difference. The minuend is the number that is subtracted from the other. The subtrahend is number from which the minuend is to be subtracted. The difference is he result obtained by subtracting the subtrahend from the minuend. The minus sign denotes the subtraction process. Basically, subtraction is the opposite process of addition.
Horizontal Method
Just like in single-digit addition, the horizontal method is the most frequently used method in showing the subtraction process. When the subtraction process is done horizontally, the minuend should be the first number in the equation followed by the minus sign and subtrahend.
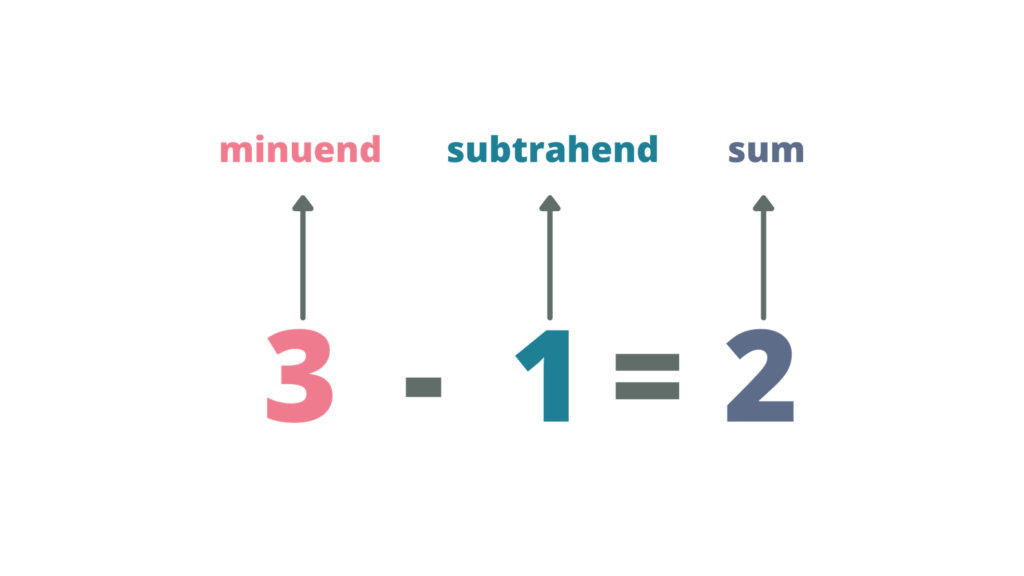
Vertical Method
When writing the subtraction process in a vertical way, the minuend should be the number on top and the subtrahend must be written below the minuend. The bar denotes the equal sign, thus it is placed below the subtrahend. Lastly, the difference should be written below the bar.
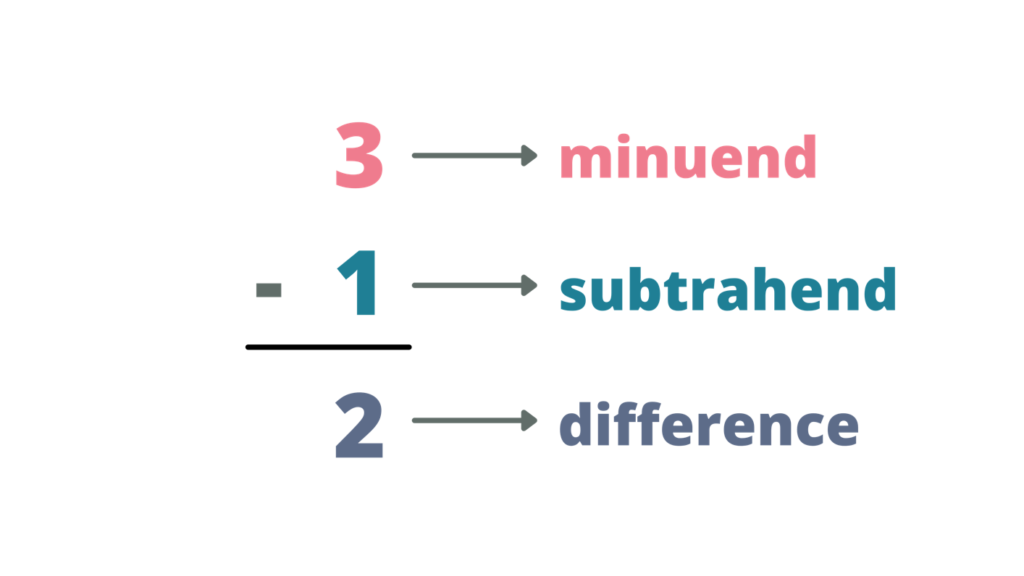
Subtracting single-digit numbers without regrouping
To subtract single-digit numbers, follow these steps:
- Write the numbers horizontally or vertically.
- Subtract the subtrahend from the minuend.
Example #1
What is the difference when 6 is subtracted from 9?
Solution
| Subtraction Process | Step-by-Step Explanation |
| 9 – 6 = | Arrange the numbers horizontally and denote the subtraction process. |
| 9 – 6 = 3 | Taking away 6 from 9 will result to 3. Thus, write 3 after the equal sign. |
| Therefore, the difference between 9 and 6 is 3. |
Example #2
Find the result of subtracting 2 from 7.
Solution
| Subtraction Process | Step-by-Step Explanation |
| 7 – 2 = | Arrange the numbers horizontally and denote the subtraction process. |
| 7 – 2 = 5 | Taking away 2 from 7 will result to 2. Thus, write 2 after the equal sign. |
| Therefore, the difference between 7 and 2 is 5. |
Example #3
What is 5 – 1?
Solution
| Subtraction Process | Step-by-Step Explanation |
| 5 – 1 = | Arrange the numbers horizontally and denote the subtraction process. |
| 5 – 1 = 4 | If we remove 1 from 5, the result is 4. Thus, write 4 after the equal sign. |
| Therefore, the result of subtracting 1 from 5 is 4. |
Example #4
What is the result of subtracting 2 from 2?
Solution
| Subtraction Process | Step-by-Step Explanation |
| 2 – 2 = | Arrange the numbers horizontally and denote the subtraction process. |
| 2 – 2 = 0 | If we subtract 2 from 2, the result is 0. Any number subtracted by the itself will always result to 0. |
| Therefore, subtracting 2 by itself will result to 0. |
Example #5
Determine the difference of subtracting 0 from 5.
Solution
| Subtraction Process | Step-by-Step Explanation |
| 5 – 0 = | Arrange the numbers horizontally and denote the subtraction process. |
| 5 – 0 = 5 | If we take away 0 from 5, the number will still remain the same. Hence, the answer is 5. |
| Therefore, if we subtract 0 from 5, the result is 5. |
These are the things that you need to remember when it comes to subtraction:
- Any number subtracted by itself will always result to zero.
- If a number is subtracted by zero, the result will be the number itself.
How to solve problems involving single-digit numbers?
When given a word problem involving single-digit numbers, follow these steps:
- Analyze the problem.
- List the information provided.
- Set up the addition or subtraction process.
- Label the answer correctly.
Example #1
Liezel have 9 headbands. Her little sister asked for two headbands. How many headbands does Liezel have now?
Solution
The problem states that Liezel’s sister is asking for two headbands. Hence, taking away will require us to use the subtraction process. The figure below shows how we can illustrate the given problem.
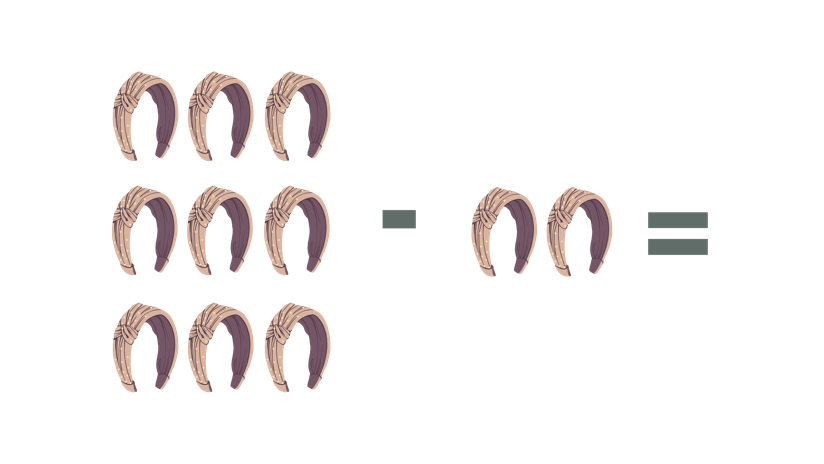
| Subtraction Process | Step-by-Step Explanation |
| 9 – 2 = | Arrange the numbers horizontally and denote the subtraction process. |
| 9 – 2 = 7 | Taking away 2 from 9 will result to 7. Then, write the difference after the equal symbol. |
| Therefore, after giving away 2 headbands, Liezel now have 7 headbands. |
Example #2
Ruby needed 5 mangoes for her mango cake and 3 mangoes for her smoothies. How many mangoes does she need to buy?
Solution
The given problem states that Ruby needs 5 mangoes for her cake and an additional 3 mangoes for her smoothies. Hence, we will use addition. The figure below shows how we can illustrate the given problem.
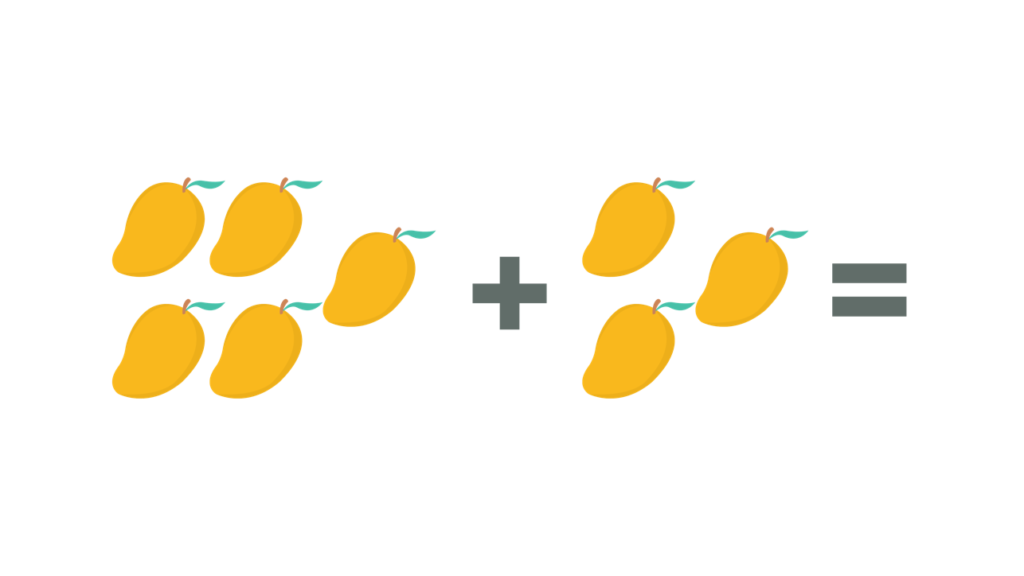
| Addition Process | Step-by-Step Explanation |
| 5 + 3 = | Arrange the numbers horizontally and denote the addition process. |
| 5 + 3 = 8 | Adding 5 and 3 will result to 8. |
| Therefore, Ruby bought 8 mangoes to make cake and smoothies. |
Example #3
Janina received 9 sunflowers from her brother. The next day, she received five additional sunflowers from her dad. How many flowers did Janina receive?
Solution
The given problem states that Janina received 9 sunflowers and an additional 5 sunflowers the next day. The keyword in the problem is the word “additional”. Hence, we will use addition. The figure below shows how we can illustrate the given problem.
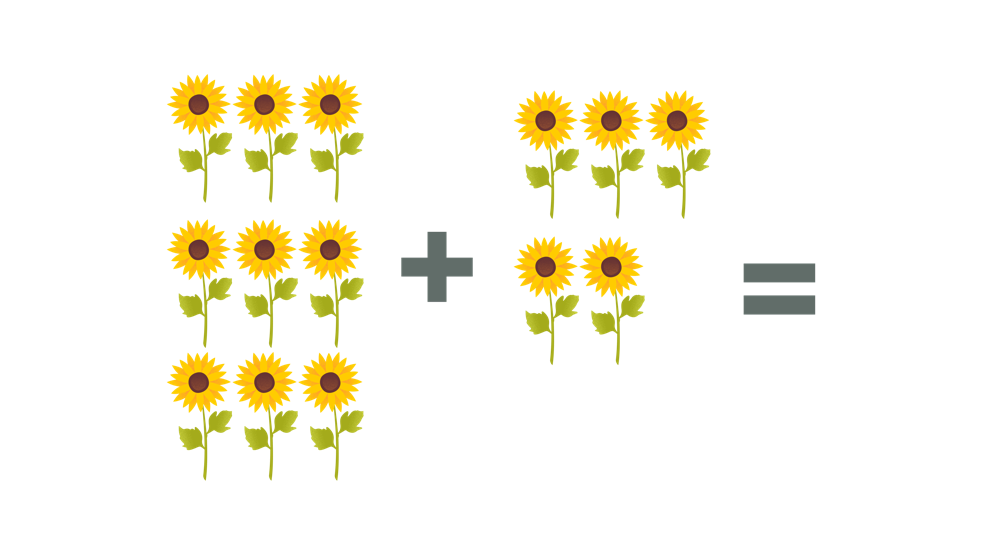
| Addition Process | Step-by-Step Explanation |
 | Arrange the numbers in a column form with the place values lined up. |
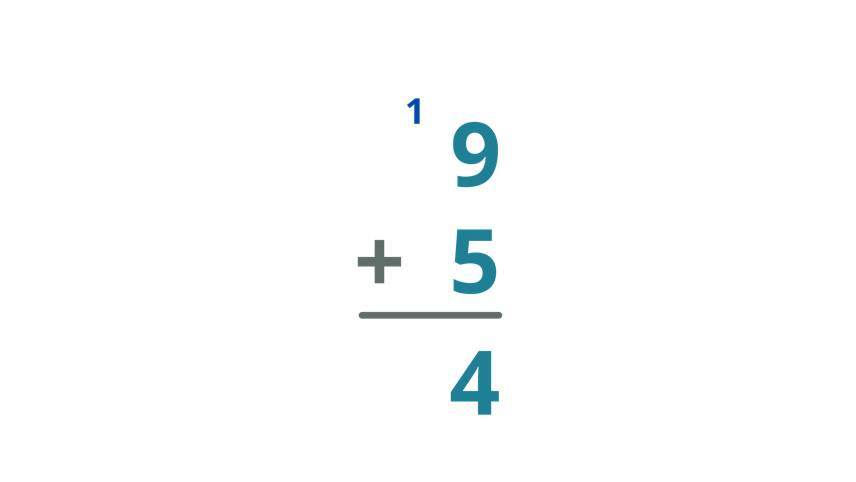 | Add the numbers in the column of the units digit. Thus,9 + 5 = 14 Since the sum of 9 and 5 is 14, write 4 below the bar and put the carry over on the tens column. |
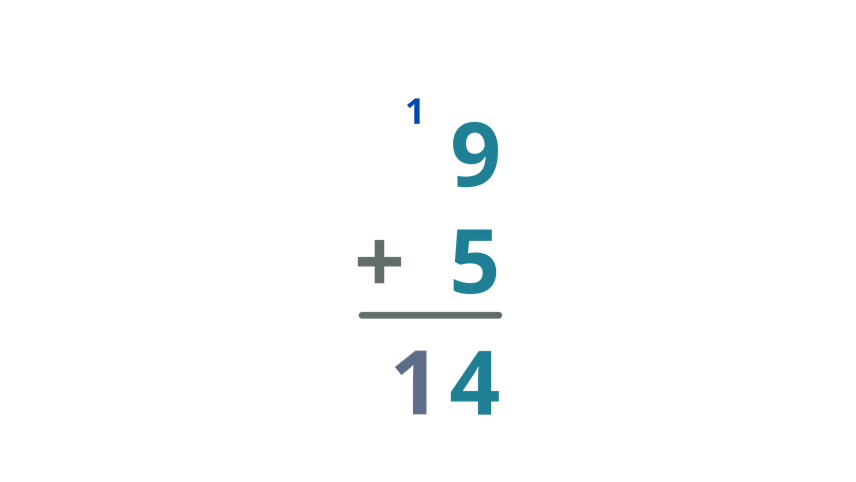 | Bring down the carry over and write it below the bar. |
| Therefore, Janina received a total of 14 sunflowers from her brother and dad. |
Example #4
Taylor have \$6. Olivia borrowed \$2 from her. How much money does Taylor have after giving \$2 to Olivia?
Solution
The problem states that Olivia borrowed \$2 from Taylor. The keyword in the problem is the word “borrowed”. Hence, we will use subtraction. The figure below shows how we can illustrate the given problem.
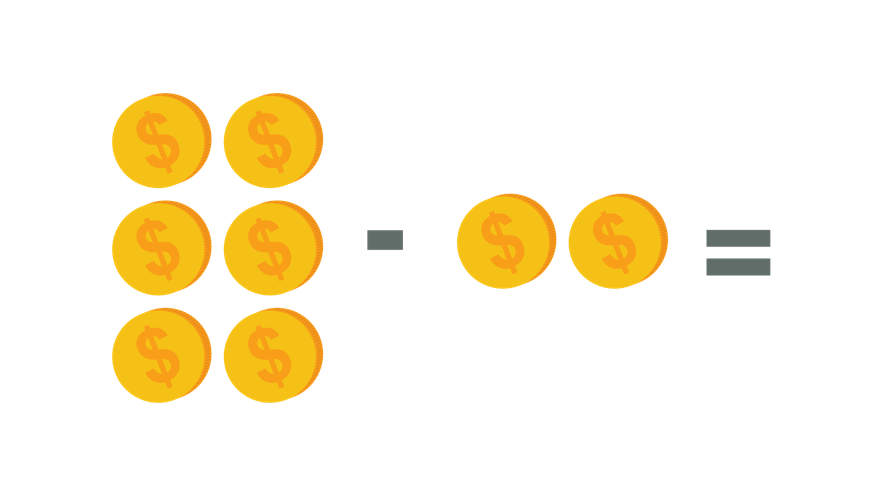
| Subtraction Process | Step-by-Step Explanation |
| 6 – 2 = | Arrange the numbers horizontally and denote the subtraction process. |
| 6 – 2 = 4 | Taking away 2 from 6 will result to 4. Then, write the difference after the equal symbol. |
| Therefore, Taylor now have $4 left. |
Example #5
Giselle bought 8 bags as a gift for herself on her birthday. Then, she received 7 bags from her friends. How many bags did Giselle received on her birthday?
Solution
In the problem, the keyword is “received”. Hence, we will use the process of addition.
| Addition Process | Step-by-Step Explanation |
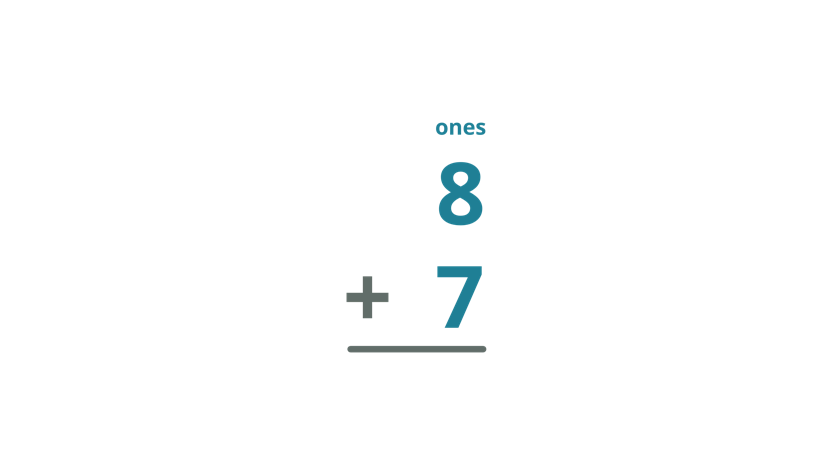 | Arrange the numbers in a column form with the place values lined up. |
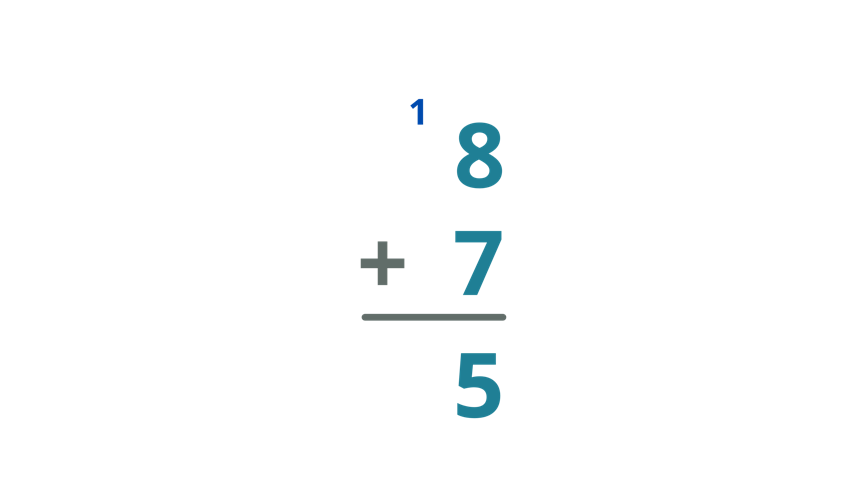 | Add the numbers in the column of the units digit. Thus,8 + 7 = 15 Since the sum of 8 and 7 is 15, write 5 below the bar and put the carry over on the tens column. |
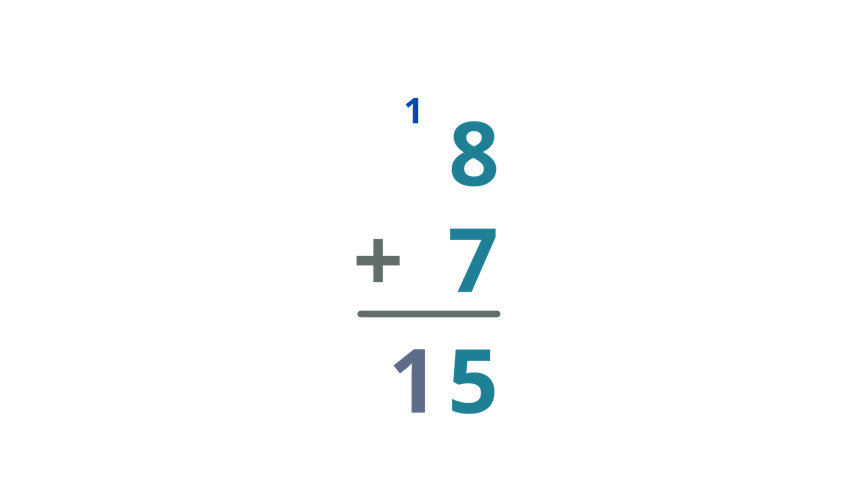 | Bring down the carry over and write it below the bar. |
| Therefore, Giselle received a total of 15 bags on her birthday. |
What are the techniques in teaching single-digit addition and subtraction?
After early learners develop a basic sense of numbers, addition is the first significant mathematical step. Subtraction, on the other hand, is the opposite of addition. Here’s a list of techniques of how you can teach single-digit addition to your students or kids.
- The use of counting manipulatives – Utilizing countable manipulatives or physical objects will help make addition and subtraction more concrete and understandable. It is critical to use a variety of methods so that students develop an understanding of the concept regardless of what is being counted. Counting with your fingers is the most intuitive way to begin, followed by tokens, bottle caps, or paper cutouts.
- Use of number lines – At this point, the majority of students will continue to add by counting out each number in a sum in order to arrive at the total solution. A number line, on the other hand, eliminates the need to count out the first digit of the sum.
- Number Bonds – Number bonds is one of the foundations in Singaporean Math. This strategy shows the “part-part-whole” relationship of numbers in terms of visual representation.
- Pairing numbers by ten – This is a mental math trick that will help students develop their procedural fluency. Instead of adding two numbers together as they are, encourage students to add them up to 10, and then add the remainder to that 10. You can assist students in developing this skill by using manipulatives. On a sheet of paper, create two rows of ten boxes, one above the other, and instruct students to fill them with manipulatives to represent the sum.
Recommended Worksheets
Addition of Single-Digit Numbers (Ages 4-5) Worksheets (United Nations’ Day)
Subtraction of 1- Digit Numbers (Family Fit Lifestyle Month Themed) Math Worksheets
Multiplication of 1-Digit Numbers (Mother Earth Day Themed) Worksheets









