Area Calculator. Use our area calculator to find the area Area of different types of Shapes with a given Radius Or Diameter. Includes, square, hexagon, triangle, kite and many more. Fantastic math tool. Click below to utilise it right now.
What is the area?
The amount of space covered by a flat surface or piece of land or an object is called its area. The shaded part of each of the following figures shows the amount of space covered by each of them on a sheet of paper.
How to find the area of a square?
. For a square whose side is of ‘s’ units –
Area of a Square = Side x Side = s2 sq. units
For example, if we have a square whose one side is 6 cm, its area would be calculated as
Area = Side x Side = 6 x 6 = 36 cm2
How to find the area of a square using the area calculator?
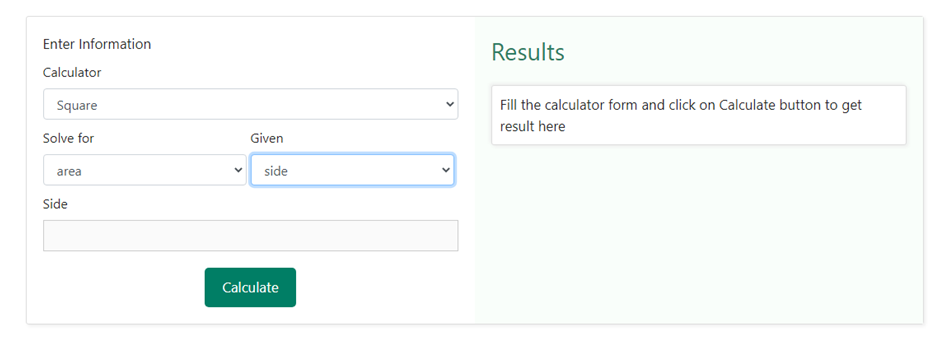
Finding the area of a square using our area calculator is quite simple. You need to first select a square from the drop-down options given in the calculator section and then select the area from the drop-down option in the solve for the section as shown below –
Now, upon entering 6 as the side in the given section of the square calculator, we will get,
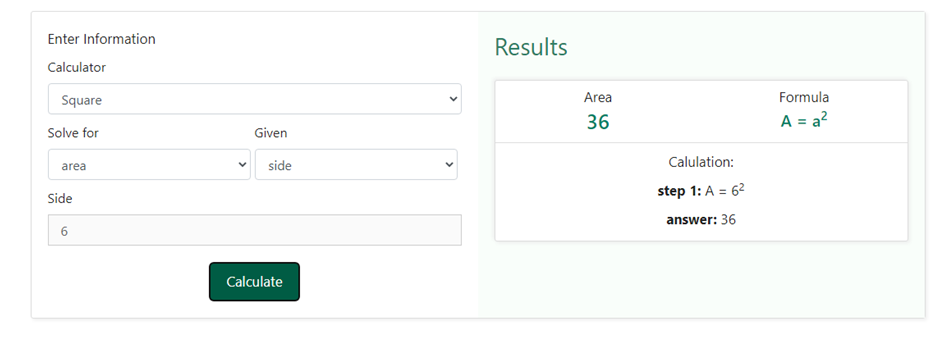
We can clearly see that in the results section, we have got the same result as we did when we used the formula ourselves. This is not enough. We can also find the area of a square when we do not know the side but are aware of the length of its diagonals.
How to find the area of a rectangle?
The area of a rectangle depends upon its length and breadth. The area of a rectangle is basically the product of its length and breadth.
The formula for finding the area of a rectangle is given by –
Area of a rectangle = Length x Breadth
How to find the area of a rectangle using the area calculator?
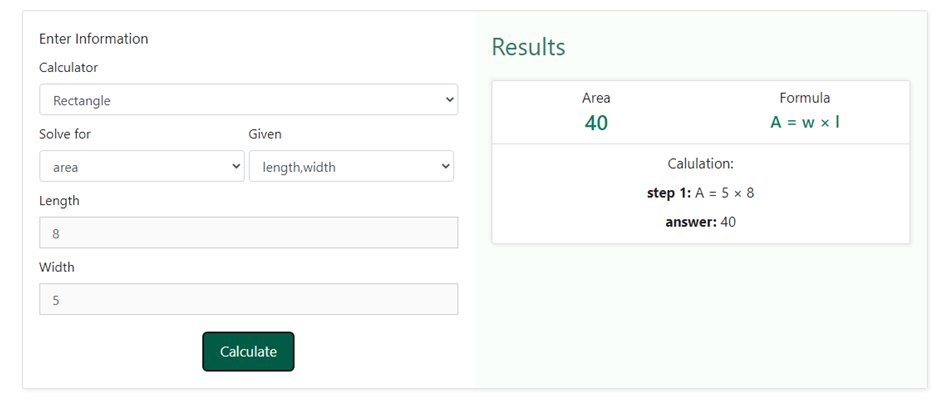
Finding the area of a rectangle using our area calculator is quite simple. You need to first select a rectangle from the drop-down options given in the calculator section and then select the information available for finding the area. There can be multiple options to choose from such as length and width, length and diagonal, length and perimeter etc. Let us take an example, where we have been given the length of the rectangle as 8 cm and the width of the rectangle as 5 cm. In order to enter these values, we shall select the option length, width in the drop-down section of the “Given” box in the area calculator. Below is a snapshot of how the drop-down box would like upon choosing length, width as selection –
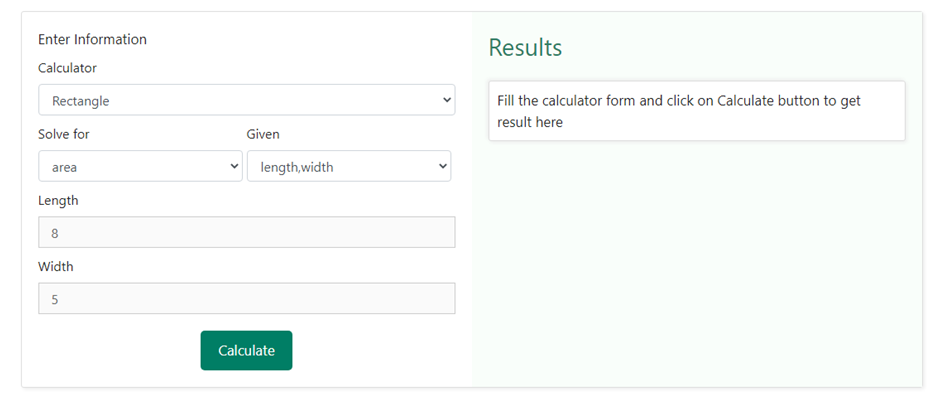
Now that we have chosen both what is required and what is given, we need to click on the calculate button. As soon as we click on the calculate button, we shall be shown the result on the right-hand side of the information that we entered in the above steps. Below is a snapshot of how the result would be displayed once we click on the calculate button-
How to find the area of a triangle?
In general, the area of a triangle is defined by 1/2 x b x h
Area of a triangle = 1/2 x b x h
where b = base of the triangle (or any one side of the triangle), and
H = Height of the triangle from that base (or side)
Let us understand this more through an example. Suppose we have a triangle that has one side as 6 cm and an altitude (height) of 8 cm on that base.
The area of this triangle is given by
1/2 x b x h
Where b = 6 cm and h = 8 cm
Therefore, Area = 1/2 x 6 x 8 = 24 cm2
How to find the area of a triangle using the area calculator?
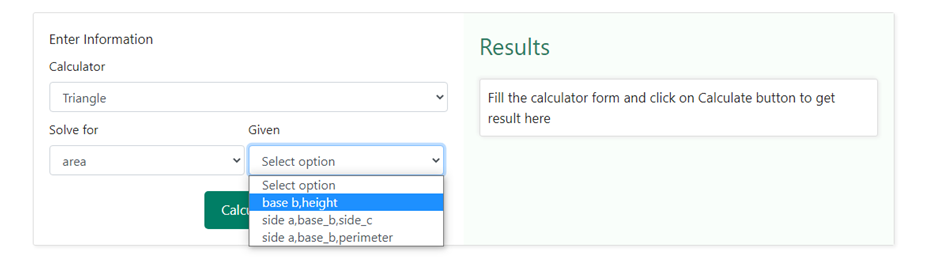
Finding the area of a triangle using our area calculator is quite simple. You need to first select a triangle from the drop-down options given in the calculator section and then select the information available for finding the area. There can be multiple options to choose from such as base and height, all the three sides, two sides and the perimeter etc. Let us take an example, where we have one side as 6 cm and an altitude (height) of 8 cm on that base.In order to enter these values; we shall select the option base and height in the drop-down section of the “Given” box in the area calculator. Below is a snapshot of how the drop-down box would like upon choosing base and height as selection –
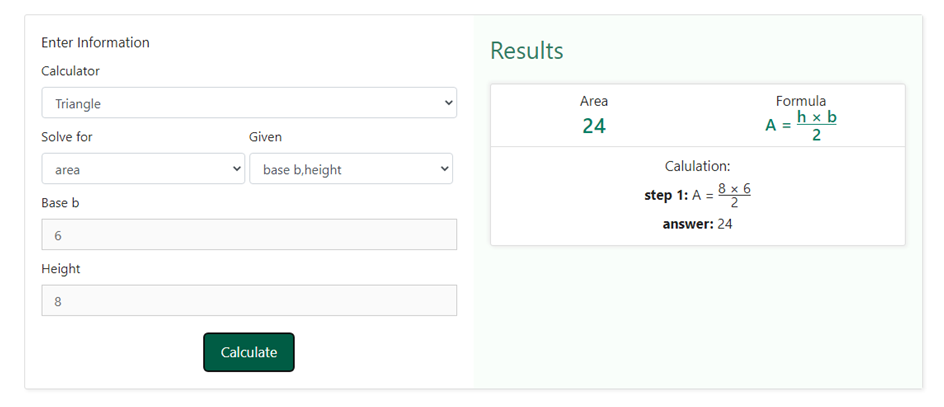
Now that we have chosen both what is required and what is given, we need to click on the calculate button. As soon as we click on the calculate button, we shall be shown the result on the right-hand side of the information that we entered in the above steps. Below is a snapshot of how the result would be displayed once we click on the calculate button-
How to find the area of a circle?
The area of a circle having a radius ‘r’ (The distance from the centre to a point on the boundary) is given by πr2 where π = 22/7 or 3.14 (approx.)
Let us understand it through an example. Suppose we have a circle that has a radius of 7 cm. Its area will be given by –
Area = πr2 = 22/7 x 7 x 7 = 154 cm2
How to find the area of a circle using the area calculator?
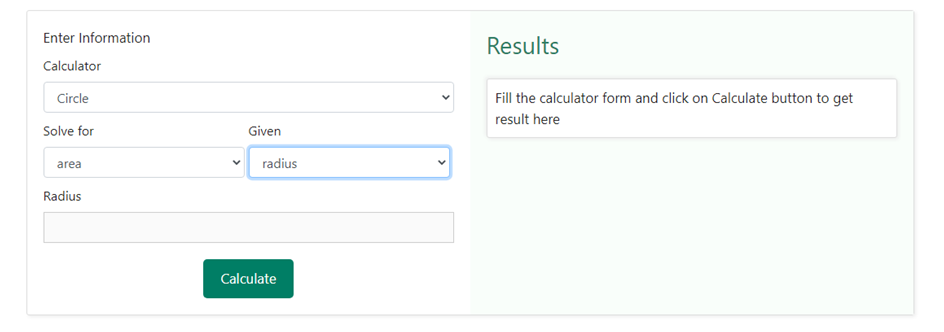
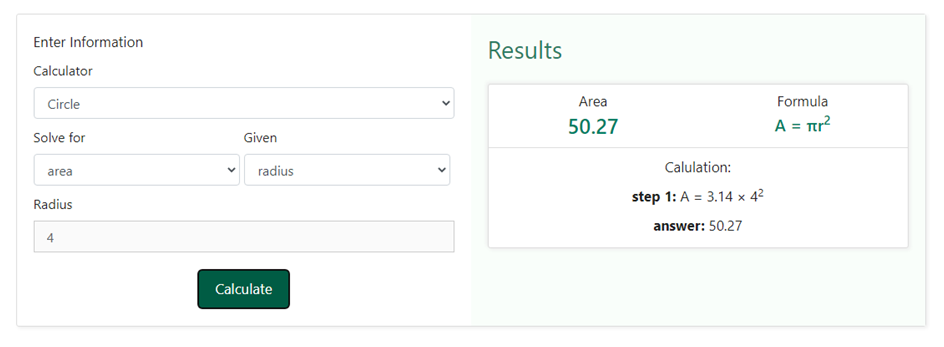
In order to find the area of a circle using the area calculator, you need to first select circle from the drop-down options given in the calculator section and then select the information available for finding the area. There can be multiple options to choose from such as radius or diameter. Let us take an example, where we have the radius of a circle as 4 cm. In order to enter these values; we shall select the option radius in the drop-down section of the “Given” box in the area calculator. Below is a snapshot of how the drop-down box would like upon choosing radius as selection –
Now that we have chosen both what is required and what is given, we need to click on the calculate button. As soon as we click on the calculate button, we shall be shown the result on the right-hand side of the information that we entered in the above steps. Below is a snapshot of how the result would be displayed once we click on the calculate button-
Similar to the above, using the area calculator we can find the area of other geometrical figures such as ellipse, parallelogram, rhombus, trapezoid and other polygons.