Download Factoring and Expanding Linear Expressions with Rational Coefficients Worksheets
Click the button below to get instant access to these premium worksheets for use in the classroom or at a home.

This worksheet can be edited by Premium members using the free Google Slides online software. Click the Edit button above to get started.
Download free sample
Not ready to purchase a subscription yet? Click here to download a FREE sample of this worksheet pack.
Definition:
Factoring and expanding linear expressions are two ways to simplify algebraic expressions. Factoring can be done with the concept of greatest common factor while expanding can be done with the application of distributive property.
Summary:
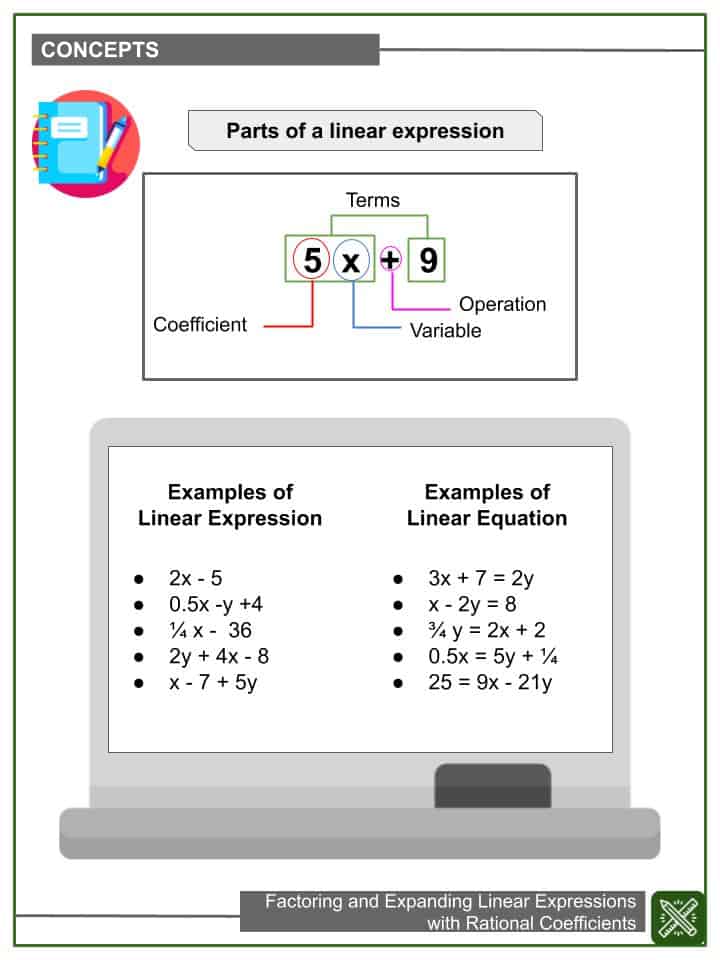
Recall: A linear expression is an algebraic expression that contains variable with a maximum power of 1. A linear expression forms a straight line when graphed in a cartesian plane.
Greatest Common Factor (GCF)
GCF is the highest factor that is common in two or more numbers.
Distributive Property
Distributive property allows us to remove the parentheses of the given algebraic equation to transform it to its simplified form.
Examples:
Greatest Common Factor
18x+24
Factors of 18: 1, 2, 3, 6, 9, 18
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Common factors: 1, 2, 3, 6
Greatest Common Factor: 6
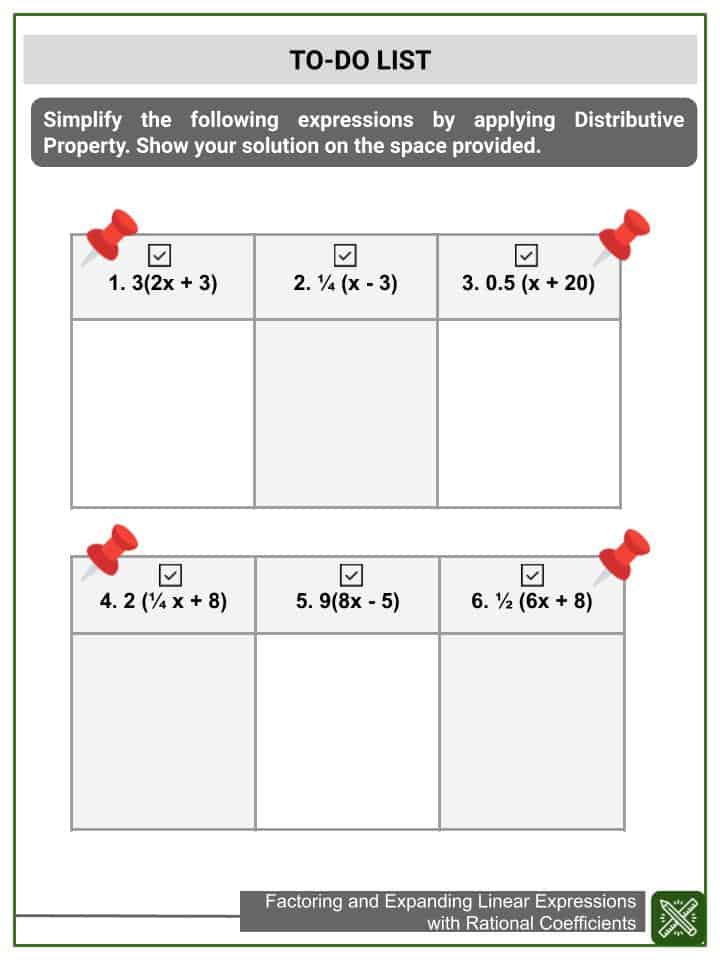
Distributive Property
2 (x + 4 ) = 2x + 8
Factoring and Expanding Linear Expressions with Rational Coefficients Worksheets
This is a fantastic bundle which includes everything you need to know about Factoring and Expanding Linear Expressions with Rational Coefficients across 15+ in-depth pages. These are ready-to-use Common core aligned Grade 7 Math worksheets.
Each ready to use worksheet collection includes 10 activities and an answer guide. Not teaching common core standards? Don’t worry! All our worksheets are completely editable so can be tailored for your curriculum and target audience.
Resource Examples
Click any of the example images below to view a larger version.