We have seen here when graphing linear relationships that the equation for a straight line can be given in the form y = mx + b. This form is known as the Slope Intercept Form and it is a most useful form as it immediately shows two important things about any straight line when graphed on a Cartesian plane; the slope m, and the y-intercept b.
There are other forms of the equation of a straight line and the examples below will show how to convert from these to the slope intercept form.
There is more here on the slope of a line so we will start by looking at the y-intercept.
The y-intercept
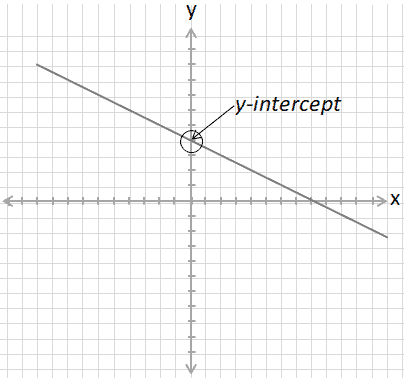
The y-intercept is the point at which a straight line intersects the y-axis. At this intersection point the value of x is always 0 so the y-value can be found algebraically simply by substituting 0 for x in the equation that represents the line as the example below shows.
Move that intercept!
Try the graph generator with different values for the y-intercept (and the slope too if you wish) to see the effect on the line.
Enter slope(m) and y-intercept(b) below then click Draw Line
Drawing equation y = 2x – 1
Click Draw Line to graph the equation
Finding the y-intercept
As shown earlier, finding the y-intercept is straightforward if the equation of the line is given in slope intercept form. e.g. for a line with equation y = 3x – 7, the y-intercept is at point (0, -7). If the equation is given in a different form then it can require additional steps as the two examples below show:
Example #1
| Find the y-intercept for line with equation 3x + 4y = 12 | |
| substitute 0 for x | (3 x 0) + 4y = 12 4y = 12 |
| Divide both sides by 4 to isolate y | 4y ÷ 4 = 12 ÷ 4 y = 3 |
| y-intercept is at point (0,3) | |
Example #2
| Find the y-intercept for line with equation 5x + 7y = -14 | |
| substitute 0 for x | (5 x 0) + 7y = -14 7y = -14 |
| Divide both sides by 7 to isolate y | 7y ÷ 7= -14 ÷ 7 y = -2 |
| y-intercept is at point (0,-2) | |
Slope Intercept Form
The equation of a straight line can be given in different forms. The form y = mx + b is the most common and is known as the Slope Intercept Form. It is not the only form though; for example the equation ax + by = c is shown in what is known as standard form.
Two benefits of the slope intercept form is that both the slope (m) and the y-intercept (b ) are immediately obvious. Let us convert the example above from standard form to slope intercept form:
Converting to Slope Intercept Form
Example #1
| Convert 3x + 4y = 12 into Slope Intercept Form | |
| subtract 3x from both sides | 3x – 3x + 4y = -3x + 12 4y = -3x + 12 |
| Divide both sides by 4 to isolate y | 4y ÷ 4= (-3x ÷ 4) + (12 ÷ 4) y = (-3/4)x + 3 y = -0.75x + 3 |
Example #2
| Convert -5x + 2y = 15 into Slope Intercept Form | |
| add 5x to both sides | 5x – 5x + 2y = 5x + 15 2y = 5x + 15 |
| Divide both sides by 2 to isolate y | 2y ÷ 2= (5x ÷ 2) + (15 ÷ 2) y = (5/2)x + 7.5 y = 2.5x + 7.5 |
Solving Other Problems
| What is the equation of a line that passes through point (5,6) and has a slope of 3? | |
| Substitute (5,6) for x and y and 3 (slope) for m in the equation in slope intercept form (y = mx + b) | 6 = (3×5) + b 6 – 15 = b b = -9 |
| Use the values of m and b to write the equation | y = 3x – 9 |
Worksheets
Use the worksheet(s) below for practice.
- Slope Intercept Form – e.g. y = mx + b (2-Pages)
- Converting to Slope Intercept Form – (2-Pages)









