Equations of Parallel and Perpendicular Lines

First, establish the slope of a line using the available data before you can derive the equation of a parallel or perpendicular line.

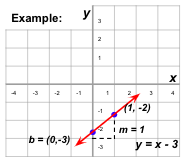
Slope-Intercept Form

y = mx + b

• m is the slope of the line, representing the rate of change between the variables x and y.
• b is the y-intercept, representing the point at which the line crosses the y-axis.
• x and y are the variables that define the points on the line.

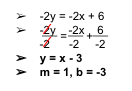
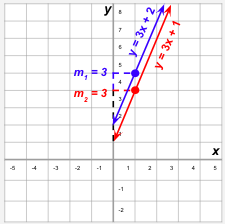
Parallel Lines

What are parallel lines?

Parallel lines are lines in a plane that never cross each other and are always equally spaced apart. The slopes of parallel lines are the same: m₁ = m₂

Equation of Parallel Lines

Example 1. Find an equation of a line parallel to y = 3x+1.

1. Identify the slope (m) of the given line.

Given line: 

y = 3x + 1 

Slope is: m = 3

2. Choose a new y-intercept c for the parallel line. c = 2
3. Write the equation of the parallel line using the same slope (m) and the new y-intercept (c). y = 3x + 2
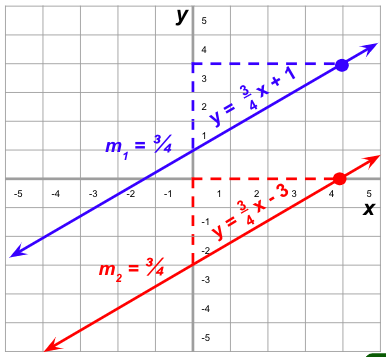
4. An equation of a line parallel to y = 3x + 1 is y = 3x + 2.

Example 2. Find an equation of a line parallel to 3x-4y = 12.

1. Rearrange the expression into slope-intercept form.

y = mx + b

-4y = -3x + 12

2. Simplify the equation.

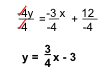
3. Keep the slope of the equation and choose a new y-intercept. For this example, let us choose (0, 1).

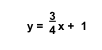
4. The equation of a line parallel 

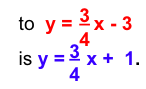
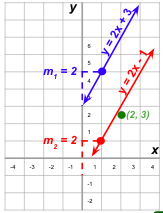
Example 3. Find the equation of the line parallel to y = 2x+3 

and passing through point (2, 3).

1. Identify the slope (m) of the given line.

Given line: y = 2x + 3 

Slope: m = 2

2. Use the point-slope form of a line to write an equation for the parallel line.

y − y₁ = m(x − x₁)

Point: (2, 3) | Slope: m = 2

3. Plug in the values from the problem into the equation. Solve for y and simplify the equation.

y – 3 = 2(x – 2)

• y – 3 = 2x – 4
• y = 2x – 4 + 3
• y = 2x – 1

4. The equation of the line parallel to y = 2x + 3 

passing through point (2, 3) is y = 2x – 1.

Perpendicular Lines

What are perpendicular lines?

Two lines that form a 90-degree angle at their intersection are said to be perpendicular. In other terms, the lines are orthogonal, which means they make a right angle. 

The slope of a perpendicular line in a two-dimensional Cartesian coordinate system is equal to the negative reciprocal of the slope of the primary line:

Equations Of Perpendicular Lines

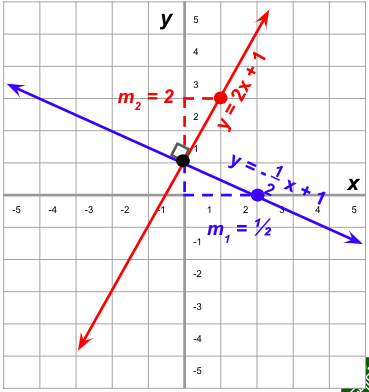
Example 1. Find the equation of a line perpendicular to y = 2x+1.

1. Identify the slope (m) of the line.

Given line: y = 2x + 1

Slope: m = 2

2. Find the negative reciprocal of the original line’s slope (m), and use it in the equation of the perpendicular line.

Slope: m = 2 

Negative reciprocal: -½ 

3. Write the equation of the perpendicular line using the new slope and any point on the line. 

For this example, let’s use the point 

(0, 1) as the y-intercept.

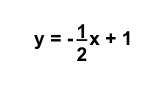
The equation of the line perpendicular 

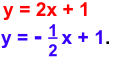
Example 2. Find the equation of a line perpendicular to 2x-3y = 6. 

1. Rearrange the equation to slope-intercept form then simplify the equation.

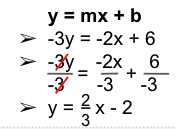
2. Find the negative reciprocal of the slope. 

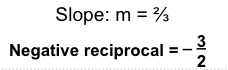
3. Write the equation of the perpendicular line using the new slope and any point. For this example, let us use (0, 1).

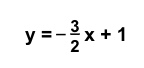
4. The line perpendicular 

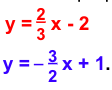
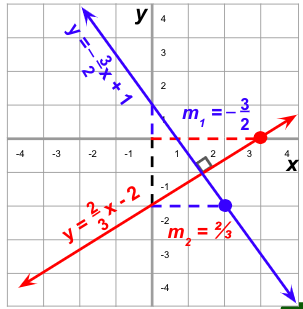
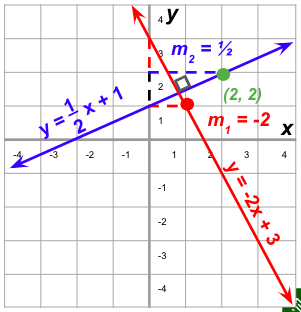
Example 3. Find the equation of a line perpendicular to 

y = -2x+3 passing through (2, 2).

1. Use the slope of the given line, which is -2.  Find its negative reciprocal.

Slope: m = -2

Negative reciprocal = ½ 

2. Use the point-slope form of a line using the points given and the negative reciprocal slope. Plug in the values from the problem into the equation and simplify.

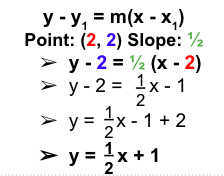
3. Write the equation of the perpendicular line using the new slope and the point given (2, 2).

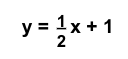
4. The equation of a line perpendicular 

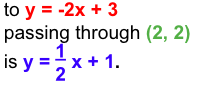
Using Equations of Parallel & Perpendicular Lines in Real Life

• Architecture & Engineering
• Technology
• Navigation
• Surveying

Equations of Parallel & Perpendicular Lines & Abstract Thinking

Finding equations of parallel and perpendicular lines is related to abstract thinking in several ways:

• It involves abstract spatial cognition and the ability to visualize lines and their direction in space.
• It includes comprehending the slope, an abstract mathematical notion, and how it relates to the steepness of a line.

• Deriving the equations of the lines involves the ability to work with abstract symbols and algebraic expressions.
• The ability to reason logically and methodically is required to ascertain the abstract connections between the lines.
• It needs the ability to apply abstract mathematical ideas to practical issues, a key component of abstract thinking.

Quick Review

Utilize the provided data to calculate the slope before attempting to get the line equation. After that, use the slope-intercept form or point-slope form to get the equation by utilizing the slope and a point on the line.

Parallel Lines

• The slope is the same for parallel lines.
• One vertical line runs parallel to another vertical line.

Perpendicular Lines

• The slopes of perpendicular lines are the reciprocals of the opposite:

• A vertical line forms a right angle (90°) with a horizontal line (and vice versa).
• When two lines are perpendicular to each other, they intersect at a 90-degree angle.

Answer these exercises:

1. Find the equation of a line parallel to y = -3x + 4 and passess through (1, -3). Show your solution.
2. Find the equation of a line perpendicular to y = -3x + 4 and passes through (5, 7). Show your solution.

Recommended Worksheets

Equations of Parallel and Perpendicular Lines (Street Food Themed) Math Worksheets
Parallel and Perpendicular Lines (Songkran Festival Themed) Math Worksheets
Spatial Skill: Lines, Segments, and Rays (International Day of PWDs Themed) Worksheets