Matrix Multiplication

What is a matrix?

A matrix is defined as a rectangular array of numbers, symbols, or expressions arranged in rows and columns (plural: matrices). If the array has n rows and m columns, then it is an n×m matrix. The dimensions of the matrix are denoted by the numbers n and m.. The numbers in the matrix are referred to as their entries. 

Matrix Notation

We usually denote matrices with capital letters, such as A, B, C, and so on. 

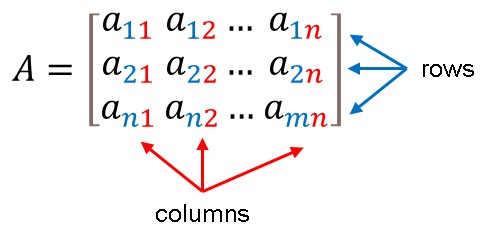
A≔ A matrix is denoted by an uppercase letter.
a≔ A matrix entry is denoted by a lower case letter.

Box brackets are commonly used to write matrices. The horizontal and vertical lines of entries in a matrix are called rows and columns, respectively. 

Dimension of a matrix

The number of rows and columns that a matrix contains determines its size.  A matrix with m rows and n columns is called an m×n matrix or m-by-n matrix, where m and n are called the matrix dimensions. When describing a matrix, you give the number of rows by the number of columns. This is sometimes referred to as the order of the matrix. For example, the matrix

A=[12       34]

is said to be a one-by-four matrix as it has one row and four columns. We could also say the order of A is 1 × 4. The matrix

B=[123   456]

is a 3×2 matrix because it has three rows and two columns. It has order 3×2.

Tip: Remember that the number of rows is given first, followed by the number of columns.

Consider the acronym “RC” for “Row then Column” to help you remember this.

What is Matrix Multiplication?

Jacques Philippe Marie Binet, a French mathematician, initially described matrix multiplication in 1812 to depict the composition of linear maps represented by matrices. As a result, matrix multiplication is a fundamental tool of linear algebra, with various applications in many fields of mathematics, including applied mathematics, statistics, physics, economics, and engineering. Computing matrix product is a fundamental process in all linear algebra computational applications.

There are only two methods for multiplying matrices. The first method involves multiplying a matrix by a scalar. This is referred to as scalar multiplication. The second method is to multiply one matrix by another. This is referred to as matrix multiplication.

Scalar Multiplication

Because the expression A+A is the sum of two matrices with the same dimensions, a matrix A can be added to itself. We end up doubling every entry in A when we compute A+A. As a result, we can interpret the expression 2A as instructing us to multiply every element in A by  2. 

In general, to multiply a matrix by a number, multiply that number by each entry in the matrix. For example,

Individual numbers are commonly referred to as scalars when discussing matrices. As a result, we refer to the operation of multiplying a matrix by a number as scalar multiplication.

Dot Product

To multiply one matrix by another, we must first understand what the dot product is. The dot product is a method for finding the product of two vectors, also known as vector multiplication. Assume the following two vectors:

u=[123] , v=[456]

To multiply these two vectors, simply multiply the corresponding entries and add the resulting products.

u∙v=(1)(4)+(2)(5)+(3)(6)
=4+10+18
=32

As a result of multiplying vectors, we get a single value. Take note, however, that the two vectors have the same number of entries. What if one of the vectors contains fewer entries than the other?

 For example, let

u=[214] , v=[310     2]

When corresponding entries were multiplied and were added together, the solution would be:

u∙v= [214] [310     2]
=2(3)+1(1)+0(4)+?(2)

There is an issue here. The first three entries of the dot product have corresponding entries to multiply with, but the fourth does not.  This means that the dot product of these two vectors cannot be computed.

As a result, the dot product of two vectors with different numbers of entries cannot be found. They must both contain the same number of entries.

What are the conditions for Matrix Multiplication?

When we want to multiply matrices, we must first ensure that the operation is possible – which is not always the case. Furthermore, unlike number arithmetic and algebra, even when the product exists, the order of multiplication can affect the outcome.

Learning the dot product is essential in multiplying matrices. When multiplying one matrix by another, the rows and columns must be treated as vectors. 

Example 1:  Find AB if A=[1234] and B=[5678]

A∙B= [1234]^.[5678]

Focus on the following rows and columns

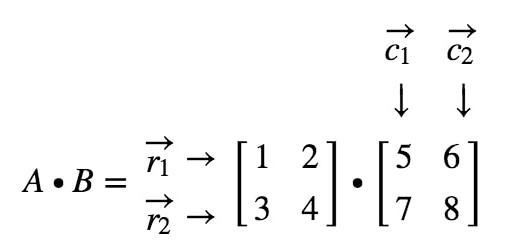
where r₁ is the first row, r₂ ​ is the second row, and c₁, c₂ ​ are first and second columns. Treat each row and column as a vector.

Notice here that multiplying a 2×2 matrix with another 2×2 matrix gives a 2×2 matrix. Thus, the matrix we get should have four entries.

See that the first entry is located on the first row and first column. So, to get the value of the first entry, simply take the dot product of r₁ and c₁.  Thus, the first entry will be

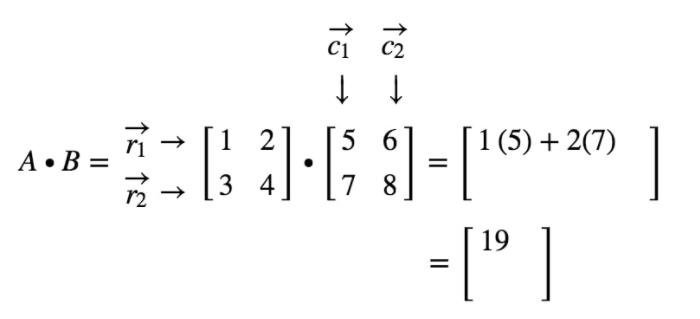
Now, notice that the location of the second entry is in the first row and second column. So, to get the value of the second entry, simply take the dot product of r₁ and c₂. Thus, the second entry will be

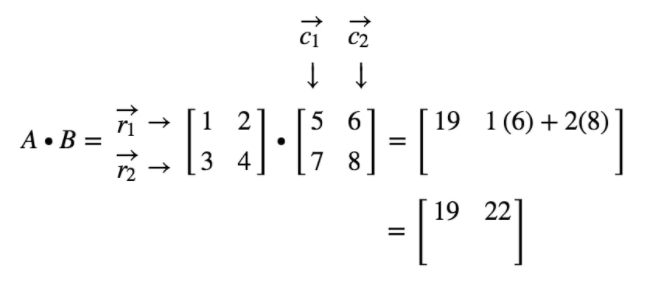
The same strategy can be used to get the value of the last two entries. 

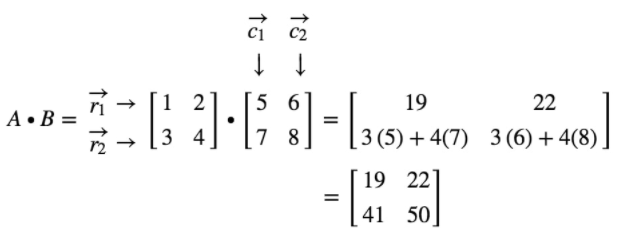
Example 2:  Find AB if A=[14   25   36] and B=[111   111   111   111]

A∙B= [14   25   36] x [111   111   111   111]

Use the dot products to compute each entry.

Hence, two matrices can be multiplied if the number of columns of the first matrix is the same as the number of rows of the second matrix. The multiplication produces another matrix with the same number of rows as the first and the same number of columns as the second. If this is not the case, the multiplication cannot be performed.

In symbols, let A be an m×p matrix and let B be an q×n matrix. Then, the product A×B=AB will be an m×n matrix provided that p=q. If p≠q, the matrix multiplication is not defined. For example,  a 2×5 matrix cannot be multiplied by a 3×4 matrix because 5≠3, whereas it is possible to multiply a 2×5 matrix by a 5×3, and the result will be a 2×3 matrix.

What are the properties of matrix multiplication?

Matrix multiplication has some properties in common with regular multiplication. Matrix multiplication, on the other hand, is not defined if the number of columns in the first factor differs from the number of rows in the second factor, and it is non-commutative even if the product remains definite after the order of the factors is changed.

Non- commutativity 

The Non-commutativity of matrix multiplication is one of the most significant differences between real number multiplication and matrix multiplication. Hence, the order in which two matrices are multiplied matters in matrix multiplication. 

An operation is commutative if, given two elements A and B such that the product AB

is defined, then BA is also defined, AB=BA

For example,

A=[0100] and B=[0010]

then,

AB= [0100] x [0010] = [1000]

but

BA= [0010] x [0010] = [1000]

Notice that the products are not the same since AB≠BA. Hence, matrix multiplication is not commutative.

Commutativity does occur in one special case. It is when multiplying diagonal matrices of the same dimension.

Aside from this major distinction, the properties of matrix multiplication are mostly like those of real number multiplication.

Distributivity

The matrix multiplication is distributive with respect to matrix addition. That is, if A, B, C, D are matrices of respective sizes m×n,n×p, n×p, and p×q, one has left distributivity

AB+C=AB+AC

and the other has right distributivity

B+CD=BD+CD

Example1: 

Notice that AB+C=AB+AC. Now find B+CA and  BA+CA

Notice that B+CA=BA+CA. It is also notable that AB+CB+CA and that AB+AC≠BA+CA which reminds us of the non-commutativity of matrix multiplication.

Associativity

This property states that the grouping surrounding matrix multiplication can be changed.

If A, B, C are m×n , n×p and p×q matrices respectively then (AB)C=A(BC)

For example, you can multiply matrix A by matrix B and then multiply the result by matrix C, or you can multiply matrix B by matrix C and then multiply the result by matrix A.

When applying this property, keep in mind the order in which the matrices are multiplied because matrix multiplication is not commutative.

Example 1: 

We can find (AB)C as follows:

We can find A(BC) as follows:

Notice that ABC= A(BC).

Multiplicative Identity Property

The n×n identity matrix denoted I n is a matrix with n rows and n columns. The entries on the diagonal from the upper left to the bottom right are all ones, and all other entries are zeroes.

For example:

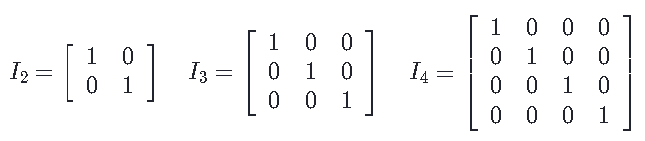
The multiplicative identity property states that the product of any n×n matrix A and I n​ is always A, regardless of the order in which the multiplication was performed. In other words, A∙I=I∙A=A

The role that the n×n identity matrix plays in matrix multiplication is like the role that the number 1 plays in the real number system. If a is a real number, then we know that a∙1=a and 1∙a=a

Multiplicative Property of Zero

A zero matrix is a matrix in which all the entries are 0. For example, the 3×3 zero matrix is O_3×3=[0 0 0 0 0 0 0 0 0]

A zero matrix is indicated by O, and a subscript can be added to indicate the dimensions of the matrix if necessary.

The multiplicative property of zero states that the product of any n×n  matrix and the n×n zero matrix is the n×n  zero matrix. In other words, A∙O=O∙A=O.

The role that the n×n zero matrix plays in matrix multiplication is like the role that the number 0 plays in the real number system. If a is a real number, then we know that a∙0=0 and 0∙a=0

The Dimension Property

The dimension property is a property that is unique to matrices. This property has two parts:

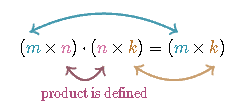
1. If the number of columns in the first matrix equals the number of rows in the second matrix, the product of the two matrices is defined.

2. If the product is defined, the resulting matrix will have the same number of rows as the first matrix and the same number of columns as the second matrix.

For example, if A is a 3×2 matrix and B is a 2×4 matrix, the dimension property tells us that the product AB is defined and AB will be a 3×4 matrix.

Where can we apply matrix multiplication?

Matrix multiplication has historically been used to simplify and clarify computations in linear algebra. This strong relationship between linear algebra and matrix multiplication continues to be fundamental in all mathematics, as well as physics, chemistry, engineering, and computer science.

The entries in a matrix can represent data as well as mathematical equations. Multiplying matrices can provide quick but accurate approximations to much more complicated calculations in many time-critical engineering applications.

Matrices emerged as a way to describe systems of linear equations, a type of problem that anyone who has taken grade-school algebra is familiar with. The term “linear” simply means that the variables in the equations have no exponents, so their graphs are always straight lines.

The equation x-2y=0, for instance, has an infinite number of solutions for both y and x, which can be depicted as a straight line that passes through the points (0,0), (2,1), (4,2), and so on. But if you combine it with the equation x -y=1, there’s only one solution: x=2 and y=1. The point (2,1) is also where the graphs of the two equations intersect.

The matrix illustrating those two equations would be a two-by-two grid of numbers, with the top row being [1 -2] and the bottom row being [1 -1], to correspond to the coefficients of the variables in the two equations.

Computers are frequently called upon to solve systems of linear equations — usually with many more than two variables — in a variety of applications ranging from image processing to genetic analysis. They’re also frequently asked to multiply matrices.

Matrix multiplication is analogous to solving linear equations for specific variables. Consider the expressions t + 2p + 3h, 4t + 5p + 6h, and 7t + 8p + 9h, which describe three different mathematical operations involving temperature, pressure, and humidity measurements. They could be represented as a three-row matrix: [1 2 3], [4 5 6], and [7 8 9].

Assume you take temperature, pressure, and humidity readings outside your home at two different times. Those readings could also be represented as a matrix, with the first set of readings in one column and the second set of readings in the other. Multiplying these matrices entails matching up rows from the first matrix, which describes the equations, and columns from the second, which represents the measurements, multiplying the corresponding terms, adding them all up, and entering the results in a new matrix. The numbers in the final matrix, for example, could predict the path of a low-pressure system.

Of course, reducing the complex dynamics of weather-system models to a set of linear equations is a difficult task in and of itself. But this brings up one of the reasons why matrices are so popular in computer science: they allow computers to do a lot of the computational heavy lifting ahead of time. Creating a matrix that produces useful computational results may be difficult, but matrix multiplication is usually not.

Graphics is one of the areas of computer science where matrix multiplication is particularly useful because a digital image is fundamentally a matrix to begin with: The matrix’s rows and columns correspond to the rows and columns of pixels, and the numerical entries correspond to the color values of the pixels. Decoding digital video necessitates matrix multiplication.  For example, some researchers were able to build one of the first chips to implement the new high-efficiency video coding standard for ultrahigh-definition TVs. The patterns they discovered in the matrices it employs have a part in this success.

Matrix multiplication can also aid in the processing of digital video and digital sound. A digital audio signal is essentially a series of numbers that represent the variation in air pressure of an acoustic audio signal over time. Matrix multiplication is used in many techniques for filtering or compressing digital audio signals, including the Fourier transform.

Another reason matrices are so useful in computer science is the graphs are as well. A graph is a mathematical construct made up of nodes, usually depicted as circles, and edges usually depicted as lines connecting them. Graphs are commonly used to represent activities of a computer program to the relationships characteristic of logistics problems.

Every graph, on the other hand, can be represented as a matrix, with each column and row representing a node and the value at their intersection representing the strength of the connection between them, which most of the time is zero. Often, converting the graphs into matrices is the most efficient way to analyze them, and solutions to graph-related problems are frequently solutions to systems of linear equations.

Recommended Worksheets

Multiplication of Functions (Travel and Tours Themed) Worksheets
Multiplication of Integers with Unlike Signs (Banking and Finance Themed) Worksheets