What is a polynomial?
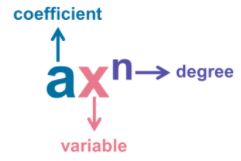
Polynomial are mathematical expressions that consist of coefficients, variables, and the operations of addition, subtraction, multiplication, and exponentiation. Specifically, polynomials are sums of monomials of the form axn, where the coefficient a can be any real number and the degree n must be a non-negative integer.
The fundamental building block of a polynomial is the monomial. A monomial is a single term: a number, a variable, a product of a number and variables, or the exponentiated product of a number and variables.
Examples of monomials:
- number: 3
- variable: y
- product of a number and variable: 3y
- product of a number and variable with an exponent: 3y2
The coefficient can be any real number, including 0. The exponent of the variables must be a non-negative integer such as 0, 1, 2, 3, and so on. Monomials cannot have variables as exponents and cannot also have variables in the denominator.
A polynomial can be the sum or difference of two or more polynomials. Each monomial separated by either plus (+) sign or minus (-) sign is called a term of a polynomial.

The leading term is the first term of the polynomial if it is in the standard form. A polynomial is said to be in standard form if the first term has the highest degree and the subsequent terms are arranged in descending order of the variable powers or exponents, followed by constant values.
The coefficient is the number multiplied to a variable. A constant is a number that has no variables.
The table below illustrates some examples of mathematical expressions that are polynomials and non-polynomials.
| Mathematical Expressions | Remarks |
| 2, x, 2x | The number 2, the variable x, and the product of 2 and x are polynomials |
| 22, x2, 2x2 | The exponentiated number 2, variable x, and 2x2 are all polynomials. |
| 5x, 2/x | 5x and 2/x are non-polynomials. Polynomials cannot have variables as exponents and denominators. |
| 5x-3, y√3 | 5x-3 and y√3 are non-polynomials. Polynomials cannot have exponents in the variables that are not whole numbers. |
| 2x2 + 3y – 5 | The expression 2x2+3y-5 is a polynomial. |
Some polynomials were specifically named according to the number of terms they contained. A polynomial with exactly one term is called a monomial. The prefix “mono” means one. A polynomial with exactly two unlike terms is called a binomial. The prefix “bi” means two. A polynomial with exactly three unlike terms is called a trinomial. The prefix “tri” means three. However, the word polynomial is a general term regardless of the number of terms, including those which only contain one term.
The table below shows some examples of monomials, binomials, trinomials, and other polynomials written in standard form.
| Monomials | Binomials | Trinomials | Other Polynomials |
| 12 | 2x + 21 | x3 − x2 + 1 | 2t4 + 9t3 − 6t2 + t |
| ½ x | 8p − 12 | 3x2 + 2x − 9 | b5 − 2b4 + ¾ b3 − 56 |
| −4y2 | 2m2 – ¾ m | 3y3 + y2 − 2 | 5x3 − 2x2 − 2x − 1 |
| 20m | 14y3 + 5y | a7+ 2a5 − 3a3 | z6 + 4z4 − 3z2 + z |
Polynomials can also be classified according to degree. The degree of a polynomial is the highest or the greatest power of a variable in a polynomial. So, the degree of 2x5 + 4x3 + 6x + 8 is 5. Suppose in case there are multiple variables in a single term. In that case, the polynomial degree is indicated by the highest or the greatest sum of powers of the variables of a term in a polynomial. When a polynomial is written in standard form, it is easy to determine the degree of the polynomial as it will be determined as the degree of the leading term.
A constant term is a term that has no variable. The degree of the constant term is 0. For example, 27 is the constant term in 5y + 27 because it has no variable attached to it. The polynomial 19y3 + 2y has no constant term, or the constant term is 0.
Like Terms and Unlike Terms
In adding or subtracting polynomials, it is essential to understand like terms first. Like terms have the exact same variable part, they must have the same variables raised to the same powers. Like terms can have a different coefficient, but the variables and their exponents must be the same. For example, 7x, 3x, and – 4x are like terms, but 9x2, 5xy, – 4xy2, y, and 6 are unlike terms. We can only combine (add or subtract) like terms.
In combining like terms, simply add the numerical coefficients and just copy the variable part. For example, the terms 3y and 4y are like terms, so they can be combined. To combine, add the numerical coefficients 3 and 4, that is, 3 + 4, then attach the variable y. Thus, 3y and 4y combined are 7y.
On the other hand, we cannot combine unlike terms into a single term. For example, the terms -4x and 2y are unlike terms because they have different variables. So, combining them will result in an expression with two terms such as -4x + 2y.
How to add polynomials?
Polynomials can be easily added using standard algebraic methods. We simply combine like terms when adding polynomials. Adding polynomials with three or more terms could be complicated to solve. In this case, polynomial addition can be done vertically where like terms are being lined up in a single column. It may help visually to line the polynomials up vertically but be sure to simplify the polynomials first before adding.
Whenever you add polynomials, keep these two rules in mind. First, when adding like terms, make sure to group them. Second, all the signs of the terms in the polynomials remain the same.
To add polynomials:
- Always see to it that the polynomials are in standard form.
- Arrange like terms vertically or horizontally.
- Add the like terms accordingly.
Example #1
What is the sum of the monomials of 2x and 4x?
Solution (Horizontal Method)
| Polynomial Addition Process | Step-by-Step Explanation |
| 2x + 4x | Set up the addition. We can see that the monomials are like terms. |
| 6x | Combine the like terms into a single term by adding their numerical coefficients. |
| Therefore, the sum of 2x and 4x is 6x. |
Solution (Vertical Method)
| Polynomial Addition Process | Step-by-Step Explanation |
| 2x + 4x ——- | Set up the addition vertically. Line up the like terms in the same column. |
2x +4x —— 6x | Combine the like terms into a single term by adding their numerical coefficients vertically. Put the answers below the bar. |
| Therefore, the sum of 2x and 4x is 6x. |
Example #2
What is the sum of the monomials of 2x and 3y?
Solution (Horizontal Method)
| Polynomial Addition Process | Step-by-Step Explanation |
| 2x + 3y | Set up the addition. Notice that 2x and 3y are unlike terms. |
| 2x + 3y | Unlike terms cannot be combined, so simply write the addition statement for the two monomials. |
| Therefore, the sum of 2x and 3y is 2x + 3y. |
Solution (Vertical Method)
| Polynomial Addition Process | Step-by-Step Explanation |
2x + 3y ——– | Set up the addition vertically. Line up the like terms in the same column. Notice that 2x and 3y are unlike terms, so they are positioned in different column. |
2x + 3y ——– 2x + 3y | Since there are no like terms to be combined, simply bring down the terms below the bar. |
| Therefore, the sum of 2x and 3y is 2x + 3y. |
Example #3
Simplify (5x – 2) + (3x + 4)?
Solution (Horizontal Method)
| Polynomial Addition Process | Step-by-Step Explanation |
| (5x – 2) + (3x + 4) | Set up the addition. |
| 5x – 2 + 3x + 4 | Remove the grouping symbols. The sign of the terms in the polynomials remains the same. |
| 5x + 3x – 2 + 4 | Arrange the terms of the new polynomial in standard form such that the like terms are beside each other. 5x and 3x are like terms. -2 and 4 are also like terms. |
| 8x + 2 | Combine the like terms into a single term by adding their numerical coefficients. |
| Therefore, (5x – 2) + (3x + 4) is equal to 8x + 2. |
Solution (Vertical Method)
| Polynomial Addition Process | Step-by-Step Explanation |
| 5x – 2 + 3x + 4 ———- | Set up the addition vertically. Line up the like terms in the same column. |
| 5x – 2 + 3x + 4 ———- 8x + 2 | Combine the like terms into a single term by adding their numerical coefficients vertically. Put the answers below the bar. |
| Therefore, (5x – 2) + (3x + 4) is equal to 8x + 2. |
Example #3
Determine the sum of 4b5 – 3b3 + 4b2 + 1 and 6b4 + 2b3 – 2b + 3.
Solution (Horizontal Method)
| Polynomial Addition Process | Step-by-Step Explanation |
| (4b5 – 3b3 + 4b2 + 1) + (6b4 + 2b3 – 2b + 3) | Set up the addition. |
| 4b5 – 3b3 + 4b2 + 1 + 6b4 + 2b3 – 2b + 3 | Remove the grouping symbols. The sign of the terms in the polynomials remains the same. |
| 4b5 + 6b4 – 3b3 + 2b3 + 4b2 – 2b + 1 + 3 | Arrange the terms of the new polynomial in standard form such that the like terms are beside each other. – 3b3 and 2b3 are like terms. 1 and 3 are also like terms. |
| 4b5 + 6b4 –b3 + 4b2 – 2b + 4 | Combine the like terms into a single term by adding their numerical coefficients. |
| Therefore, the sum of | 4b5 – 3b3 + 4b2 + 1 and 6b4 + 2b3 – 2b + 3 is4b5 + 6b4 – b3 + 4b2 – 2b + 4 |
Solution (Vertical Method)
| Polynomial Addition Process | Step-by-Step Explanation |
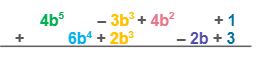 | Set up the addition vertically. Line up the like terms in the same column. |
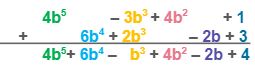 | Combine the like terms into a single term by adding their numerical coefficients vertically. Put the answers below the bar. |
| Therefore, the sum of | 4b5 – 3b3 + 4b2 + 1 and 6b4 + 2b3 – 2b + 3 is4b5 + 6b4 – b3 + 4b2 – 2b + 4. |
Example #4
Simplify (4y3 – 3y + 4) + (y5 + 6y3 + 7) + (y3 – 6y + 2)?
Solution (Horizontal Method)
| Polynomial Addition Process | Step-by-Step Explanation |
| (4y3 – 3y + 4) + (y5 + 6y3 + 7) + (y3 – 6y + 2) | Set up the addition. |
| 4y3 – 3y + 4 + y5 + 6y3 + 7 + y3 – 6y + 2 | Remove the grouping symbols. The sign of the terms in the polynomials remains the same. |
| y5 + 4y3 + 6y3 + y3 – 3y – 6y + 4 + 7+ 2 | Arrange the terms of the new polynomial in standard form such that the like terms are beside each other. 4y3, 6y3, and y3 are like terms. – 3y and – 6y are also like terms. The constants 4, 7, and 2 are also like terms. |
| y5 + 11y3 – 9y + 13 | Combine the like terms into a single term by adding their numerical coefficients. |
| Therefore, | (4y3 – 3y + 4) + (y5 + 6y3 + 7) + (y3 – 6y + 2) is equal to y5 + 11y3 – 9y + 13. |
Solution (Vertical Method)
| Polynomial Addition Process | Step-by-Step Explanation |
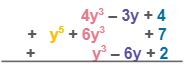 | Set up the addition vertically. Line up the like terms in the same column. 4y3, 6y3, and y3 are like terms. – 3y and – 6y are also like terms. The constants 4, 7, and 2 are also like terms. |
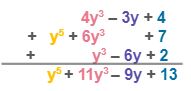 | Combine the like terms into a single term by adding their numerical coefficients vertically. Put the answers below the bar. |
| Therefore, | (4y3 – 3y + 4) + (y5 + 6y3 + 7) + (y3 – 6y + 2) is equal toy5 +11y3 – 9y + 13 |
How to subtract polynomials?
The method for subtracting polynomials is the same as the method for adding polynomials. The only difference is that when subtracting one polynomial from another, you must first find the additive inverse of the polynomial being subtracted, then combine like terms. In other words, the subtraction symbol must be distributed to the subtrahends before combining like terms. The most common error in subtracting polynomials is failing to change the sign of EVERY term in the subtrahend or the polynomials being subtracted.
Just like in addition, subtracting polynomials with three or more terms could also be complicated to solve. In this case, polynomial subtraction can also be done vertically where like terms are being lined up in a single column. If you choose to line the polynomials up vertically, be sure to simplify the polynomials first before subtracting.
To subtract polynomials:
- Always see to it that the polynomials are in standard form.
- Find the additive inverse of the polynomial being subtracted.
- Arrange like terms vertically or horizontally.
- Add the like terms accordingly.
Example #1
What is the difference between the monomials of 5xy and – 2xy?
Solution (Horizontal Method)
| Polynomial Addition Process | Step-by-Step Explanation |
| 5xy – (–2xy) | Set up subtraction. |
| 5xy + 2xy | Distribute the minus sign to the term in the subtrahend. Thus, –2xy will become 2xy. Then, proceed just like in the process of addition. |
| 7xy | Combine like terms into a single term by adding their numerical coefficients. |
| Therefore, the difference between 5xy and – 2xy is 7xy. |
Solution (Vertical Method)
| Polynomial Addition Process | Step-by-Step Explanation |
5xy – – 2xy ————— | Set up subtraction vertically. |
5xy + 2xy ————— | Distribute the minus sign to the term in the subtrahend. Thus, the –2xy will become 2xy. Then, proceed just like in the process of addition. |
5xy + 2xy ————— 7xy | Combine the like terms into a single term by adding their numerical coefficients vertically. Put the result below the bar. |
| Therefore, the difference between 5xy and – 2xy is 7xy. |
Example #2
Find the difference of 4y2 + 3y – 7 and 2y2 – 3.
Solution (Horizontal Method)
| Polynomial Subtraction Process | Step-by-Step Explanation |
| (4y2 + 3y – 7) – (2y2 – 3) | Set up subtraction. |
| 4y2 + 3y – 7 – 2y2 + 3 | Distribute the minus sign to the terms in the subtrahend. Thus, 2y2 will become –2y2, and –3 will become 3. Then, proceed just like in the process of addition. |
| 4y2 – 2y2 + 3y – 7 + 3 | Arrange the terms of the new polynomial in a standard form such that the like terms are beside each other. 4y2 and -2y2 are like terms. -7 and 3 are also like terms. |
| 2y2 + 3y – 4 | Combine the like terms into a single term by adding their numerical coefficients. |
| Therefore, the difference of | 4y2 + 3y – 7 and 2y2 – 3 is 2y2 + 3y – 4 |
Solution (Vertical Method)
| Polynomial Subtraction Process | Step-by-Step Explanation |
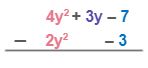 | Set up the subtraction vertically. Line up the like terms in the same column. 4y2 and –2y2 are like terms. – 7 and – 3 are also like terms |
 | Distribute the minus sign to the terms in the subtrahend. Thus, 2y2 will become –2y2, and –3 will become 3. Then, proceed just like in the process of addition. |
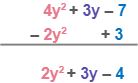 | Combine the like terms into a single term by adding their numerical coefficients vertically. Put the result below the bar. |
| Therefore, the difference of | 4y2 + 3y – 7 and 2y2 – 3 is 2y2 + 3y – 4 |
Example #3
What is the result of (4x3 – 3x + 4) – (–6x3 + 7) – (– 6x + 2)?
Solution (Horizontal Method)
| Polynomial Subtraction Process | Step-by-Step Explanation |
| (4x3 – 3x + 4) – (–6x3 + 7) – (– 6x + 2) | Set up subtraction. |
| 4x3 – 3x + 4 + 6x3 – 7 + 6x – 2 | Distribute the minus sign to the terms in the subtrahends. Thus, –6x3 will become 6x3, and 7 will become –7, –6x will become 6x, and 2 will become –2. Then, proceed just like in the process of addition. |
| 4x3 + 6x3 – 3x + 6x + 4 – 7– 2 | Arrange the terms of the new polynomial in a standard form such that the like terms are beside each other. 4x3 and 6x3 are like terms. –3x and 6x are also like terms. The constants 4, –7 and –2 are also like terms. |
| 10x3 + 3x – 5 | Combine the like terms into a single term by adding their numerical coefficients. |
| Therefore, (4x3 – 3x + 4) – (–6x3 + 7) – (– 6x + 2) is equal to 10x3 + 3x – 5. |
Solution (Vertical Method)
| Polynomial Subtraction Process | Step-by-Step Explanation |
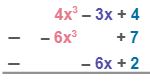 | Set up the subtraction vertically. Line up the like terms in the same column. 4x3 and 6x3 are like terms. –3x and 6x are also like terms. The constants 4, –7 and –2 are also like terms. |
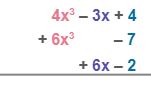 | Distribute the minus sign to the terms in the subtrahends. Thus, –6x3 will become 6x3, and 7 will become –7, –6x will become 6x, and 2 will become –2. Then, proceed just like in the process of addition. |
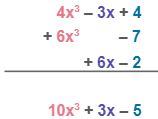 | Combine the like terms into a single term by adding their numerical coefficients vertically. Put the result below the bar. |
| Therefore, (4x3 – 3x + 4) – (–6x3 + 7) – (– 6x + 2) is equal to 10x3 + 3x – 5. |
What is the importance of adding and subtracting polynomials?
Polynomials are an essential part of the “language” of mathematics, and they are used in many real-life applications. Some of these applications, such as adding and subtracting lengths, can be obvious, while others, such as combining rates, may not. Their use in nearly every field of mathematics to express numbers as the result of mathematical operations such as addition and subtraction, among others, can be traced back to ancient times. Besides being the “building blocks” in other types of mathematical expressions, polynomials can also be used as “building blocks” in rational expressions.
Polynomials can be used to describe many mathematical processes that occur in everyday life. The cost of items on a grocery bill can be represented as a polynomial when added together. Calculating the distance traveled by a vehicle or object can be represented mathematically as a polynomial function. It is possible to think of polynomials to calculate the perimeter, area, and volume of geometric figures. Moreover, predicting sales in advance is one of the keys to running a successful business but, with so many unknowns, how can you predict revenue, cost, and profit? Variables and polynomials come in handy in these situations. These quantities can be modeled without knowing their exact values. Once you have them, it will be much easier to plug in the values and understand how they will affect the overall quantity.
Recommended Worksheets
Addition of Polynomials (Ages 11-13) Worksheets (International Women’s Day Themed)
Subtraction of Polynomials (Ages 11-13) Worksheets (Health Themed)
Multiplication of Polynomials (Universe Themed) Worksheets









