Square Calculator

Square Calculator. Find the area, side, diagonal and perimeter of a Square with our free to use calculator. Fantastic math tool. Click below to utilise it right now.

What is a Square?

A square is a quadrilateral that has four equal sides and four right angles. In other words, a square is a quadrilateral with the following properties –

1. The opposite sides of a square are parallel
2. All the four sides of the square are equal
3. Al the four angles of a square measure 90^o
4. The diagonals of a square bisect each other at 90^o
5. The diagonals of a square are equal in length

How to calculate the area of a Square?

The amount of space covered by a flat surface or piece of land or an object is called its area. For a square whose side is of ‘s’ units –

Area of a Square = Side x Side = s² sq. units

For example, if we have a square whose one side is 6 cm, its area would be calculated as

Area = Side x Side = 6 x 6 = 36 cm²

How to use the Square calculator to find the area of the square?

Finding the area of a square using our square calculator is quite simple. You need to select the area from the drop-down option as shown below –

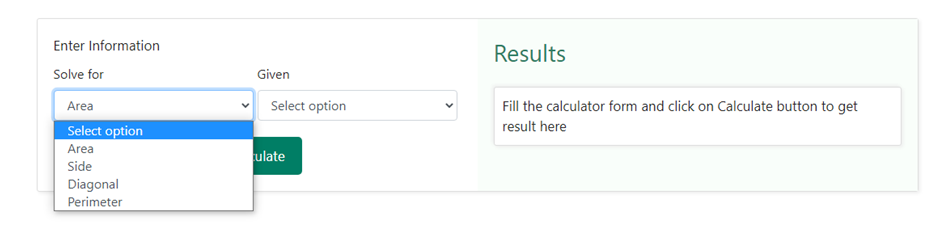
Next, you need to select “ side “ in the drop down section under the heading “ Given “ as shown below –

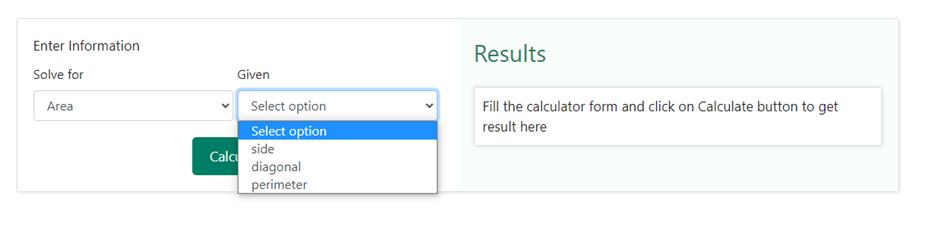
These selections indicate that you know the side of the square and want to find its area. Let us for example, consider the example that we took above, where the side of a square is  6 cm and using the formula, we found the area as Area = Side x Side = 6 x 6 = 36 cm²

Now, upon entering 6 as the side in the given section of the square calculator, we will get,

We can clearly see that in the results section, we have got the same result as we did when we used the formula ourselves. This is not enough. We can also find the area of a square when we do not know the side but are aware of the length of its diagonals. Let us see how it works out.

Finding the area of a square when we are given the Diagonal of a Square

We know that if we have a square with each side as “a” cm and each diagonal as “d” cm, then the area of a square having diagonal (d) = $\frac{d^2}{2}$. Let us take an example.

Example          Find the area of a square land a diagonal of length 10 m.

Solution          We have been given that the diagonal of the square land = 10 m

                        We know that area of a square having diagonal (d) = $\frac{d^2}{2}$

                        Hence,

Area of the square land = $\frac{10^2}{2}$ m² = $\frac{100}{2}$ m² = 50 m²

Hence, the area of a square land a diagonal of length 10 m = 50 m²

Now, let us find the same using the square calculator.

Finding the area of a square through its diagonal is quite simple when you do it through our square calculator. You need to select the area from the drop-down option as shown below –

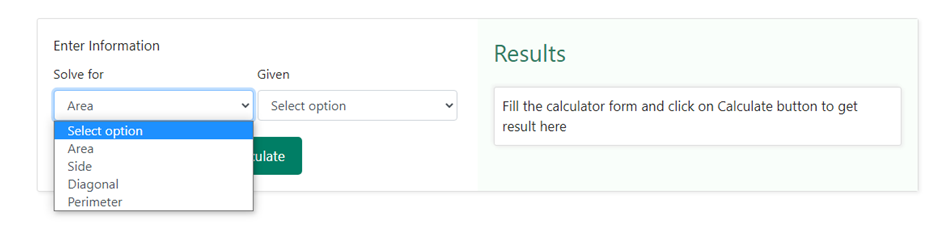
Next, you need to select “ diagonal “ in the drop down section under the heading “ Given “ as shown below –

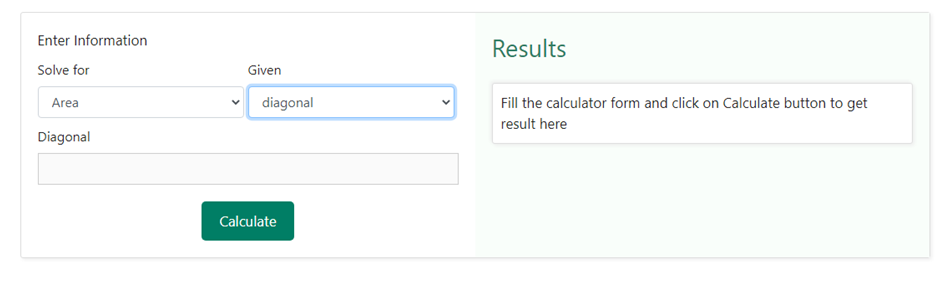
These selections indicate that you know the diagonal of the square and want to find its area.

Now, upon entering 10 as diagonal in the given section of the square calculator, we will get,

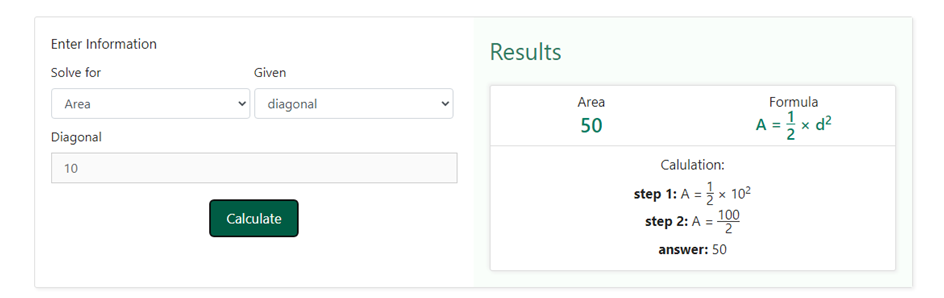
We can clearly see that in the results section, we have got the same result as we did when we used the formula ourselves.

Finding Perimeter of a Square

We know that the perimeter of a square having a side “ s” is given by

Perimeter of a Square =  4 x Side = 4 s

Let us consider an example.

Suppose we wish to find the perimeter of a square having sides of 8 cm. In order to do so, we will simply, substitute the value of s in the above formula by 8 and we will get

Perimeter of a Square = 4 x s = 4 x 8 = 32 cm.

Can we find the same using the square calculator? Of course yes, we can.

Finding the perimeter of a square through its side is quite simple when you do it through our square calculator. You need to select perimeter from the drop-down option as shown below –

Next, you need to select “ side “ in the drop-down section under the heading “ Given “ as shown below –

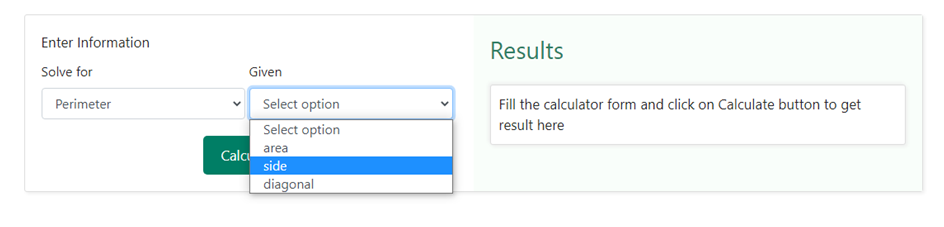
These selections indicate that you know the side of the square and want to find its perimeter.

Now, upon entering 8 as the side in the given section of the square calculator, we will get,

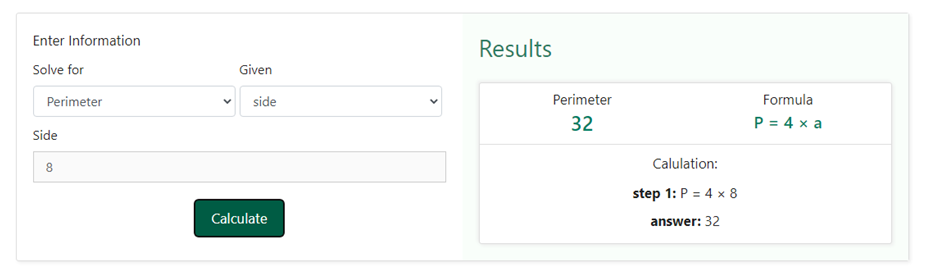
We can clearly see that in the results section, we have got the same result as we did when we used the formula ourselves.

Finding the area of a Square when we know its Perimeter

Can we find the area of a square when we know its perimeter? Let us take an example.

Example          Find the area of a square park whose perimeter is 320 m

Solution          We have been given that the perimeter of the square park is 320 m.

                        We know that

The perimeter of a Square = 4 x Side

Therefore,

320 = 4 x Side

⇒ Side = $\frac{320}{4}$ cm = 80 m

Hence, side of the square park = 80 m

Now, to find out the area of the square, we know that

Area of a Square = Side x Side = s² sq. units

Therefore,

Area of a Square Park= (80 x 80) m² = 6400 m²

Hence, the area of the square park = 6400 m²

Now, let us check the same using the square calculator.

Finding the area of a square through its perimeter is quite simple when you do it through our square calculator. You need to select the area from the drop-down option as shown below –

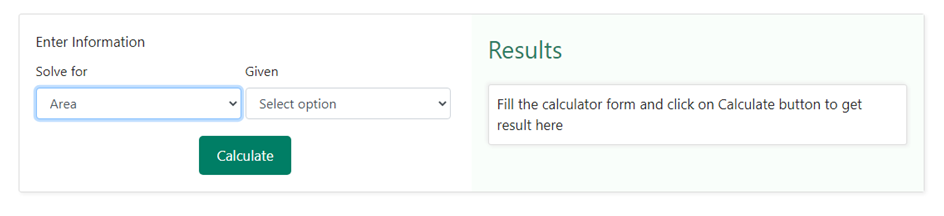
Next, you need to select “ perimeter “ in the drop-down section under the heading “ Given “ as shown below –

These selections indicate that you know the perimeter of the square and want to find its area. Now, upon entering 320 as the side in the given section of the square calculator, we will get,

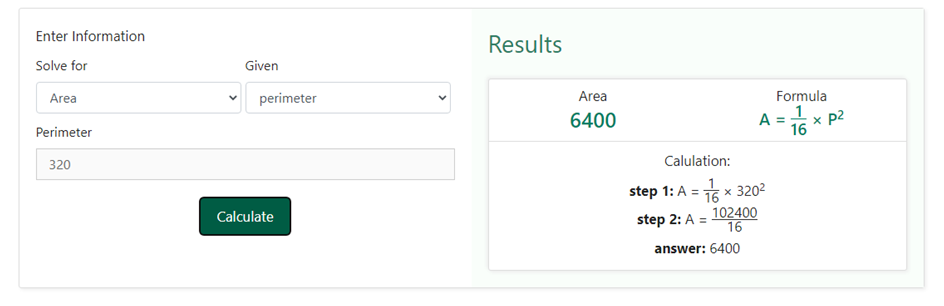
We can clearly see that in the results section, we have got the same result as we did when we used the formula ourselves. Moreover, the calculator does not just show the result. It also displays the corresponding formula that has been used to derive the result along with the steps involved in the process. this means that our square calculator not just helps you check the final result, but it also assists in the learning process where you can go through the corresponding formulas and the steps involved to obtain the desired result. Repeated use of the calculator will certainly help you have a grasp on the various aspects of finding different aspects of a square such as its area, perimeter and also help in visualisation of the placement of dimensions such as its sides and the diagonals.