Scientific Notation Calculator

What are Scientific Notations?

A scientific notation is a form of writing a given number, an equation, or an expression in a form that follows certain rules. In other words, Scientific notation is the standard way to express a number as the product of a real number and power of 10.

Addition and Subtraction of Numbers in Scientific Notations

The following steps are involved for the addition of numbers in scientific notations – 

1. Rewrite the number with the smaller exponent so that it has the same exponent as the number with the larger exponent by moving the decimal point of its decimal number.
2. Add /  Subtract the decimal numbers. The power of 10 will not change.
3. Convert your result to scientific notation if necessary.

Let us understand the above steps using an example.

Example

Suppose we have two numbers 7 . 3  x 10 ⁴ and 2 . 4 8  x 10 ⁵

We want to find the sum of these numbers. Let us see how it can be done.

Solution

We will have, ( 0 . 7 3  x 10 ⁵ ) + (2 . 4 8  x 10 ⁵ )

 = ( 0. 7 3 + 2 . 4 8 ) x 10 ⁵

= 3 . 2 1  x 10 ⁵

Example

Suppose we have two numbers 4 . 9 x 10 ³ and 1 . 3 x 10 ⁴

We want to subtract the second number from the first number. Let us see how it can be done.

Solution

We will have, ( 4 . 9 x 10 ³  ) – (1 . 3 x 10 ⁴ )

= ( 0 . 4 9 x 10 ⁴  ) – (1 . 3 x 10 ⁴ )

= ( 0 . 4 9 – 1 . 3 ) x 10 ⁴

= – 0 . 8 1 x 10 ⁴

Multiplication and Division of Numbers in Scientific Notations

Multiplication of numbers in scientific notation is different from their addition and subtraction. The following steps are involved for the multiplication of numbers in scientific notations – 

1. Obtain the decimal numbers in scientific notation.
2. Multiply / divide the decimal numbers.
3. Multiply / divide the powers of 10 by adding their exponents.
4. Convert your answer to scientific notation if necessary.

Let us understand the above steps using an example.

Example

Suppose we have two numbers ( 3 . 4  x  10 ^{– 2} ) and ( 6 . 2 x 10 ⁶ ) and we want to find their product. 

Solution

We will have, 3 . 4  x 6 . 2 = 2 1 . 0 8  …………………………. ( 1 )

Next, we will multiply the powers of 10 for which we need to add the exponents of the two decimal numbers. 10 ^{– 2} x 10 ⁶ = 10 ^{– 2 + 6}  = 10 ⁴ ………………………….. ( 2 )

From ( 1 ) and ( 2 ) we will have,

( 3 . 4  x  10 ^{– 2} ) x ( 6 . 2 x 10 ⁶ )  = 2 1 . 0 8 x 10 ⁴

We will then have, 2 1 . 0 8 x 10 ⁴ = 2 . 1 0 8 x 10 ⁵

Hence, ( 3 . 4  x  10 ^{– 2} ) x ( 6 . 2 x 10 ⁶ ) = 2 . 1 0 8 x 10 ⁵

Example

Suppose we have two numbers ( 8 . 4  x  10 ⁵ ) and ( 1 . 4 x 10 ^{– 2}  ) and we want to divide the first number by the second.  

Solution

We will have, 8 . 4 ÷ 1 . 4 = 6 ………………….. ( 1 )

 ( 10 ⁵ ) ÷ ( 10 ^{– 2} ) = 10 ^{( 5 – ( – 2 )} = 10 ^{5 + 2} = 10 ⁷ …………………………. ( 2 )

Now, we will combine the results obtained in ( 1 ) and ( 2 ) to get,

( 3 . 4  x  10 ^{– 2} ) ÷ ( 6 . 2 x 10 ⁶ ) = 6 x 10 ⁷

Hence, ( 3 . 4  x  10 ^{– 2} ) ÷ ( 6 . 2 x 10 ⁶ ) = 6 x 10 ⁷

Using the scientific notation calculator

It is quite simple to use the scientific notation calculator for performing operations involving scientific notations. The following steps are required to be followed for this purpose – 

Step 1 – The first step is to enter the details of the two scientific notations on whom an operation is to be performed. Let us take, for example, ( 3 . 4  x  10 ^{– 2} ) and ( 6 . 2 x 10 ⁶ ) to perform different operations using the calculator. So, in the first step, we will enter the first number in the box against the “ 1^st number “ in the Enter Information “ section of the calculator. Below is the snapshot providing detail of how the 1^st number will be entered – 

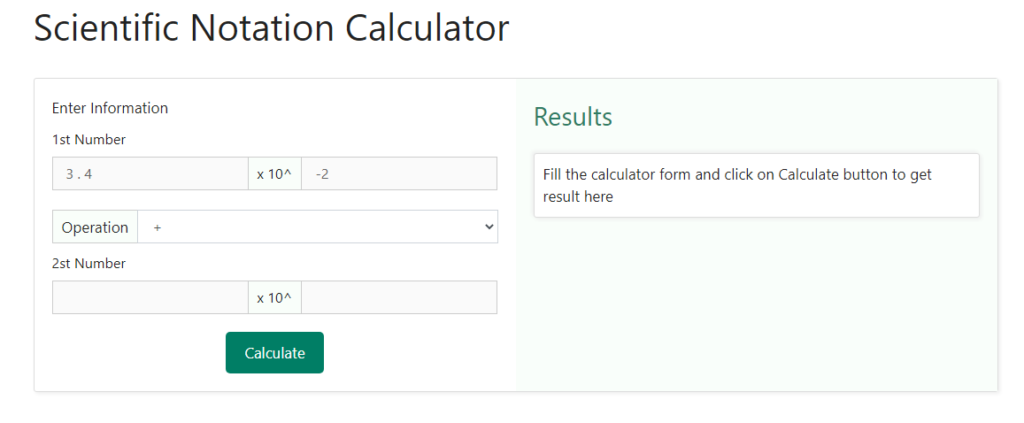
 Note here that both the decimal value and the power of 10 need to be entered separately.

Step 2 – The next step is to enter the second number in the box against the “ 2^nd number “ in the Enter Information “ section of the calculator. We will therefore enter 6 . 2 x 10 ⁶  as the second number. Below is the snapshot providing detail of how the 2^nd number will be entered – 

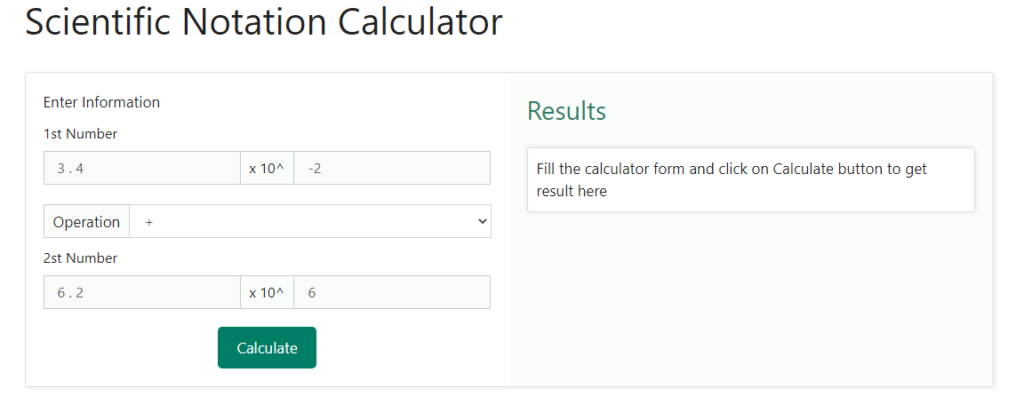
Step 3 – after entering both the numbers, we need to mention the operation we wish to perform between them. we shall select “ + “ , “ – “, “ x “ or “ ÷ “  from the drop-down menu of the operation box. Let us, for example, multiply the two numbers. We will therefore choose the “ x “ option from the drop-down menu. Below is the snapshot of what the selection would look like – 

Step 4 – Now that we have entered all the required information, our last step is to perform the calculation. For this purpose, we just need to click on the “ calculate “ button. As soon as we will click on this button, we can see the result obtained on the right-hand side of the values that we had entered in the previous steps. Below is a snapshot of how the selection would look like when we will click on the “ calculate “ button

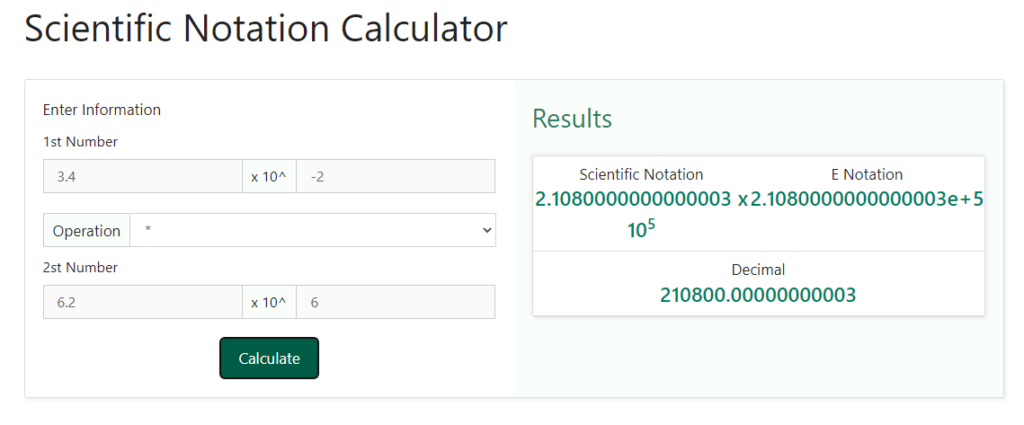
In this manner, using this scientific notation calculator, we can perform all the operations involving scientific notations.