Polygon Calculator

What is a polygon?

The shapes that are made of line segments that formed closed loops are called closed shapes. They start and end at the same point. For example, a ball is a closed shape. A simple closed figure formed of three or more line segments is called a polygon.

Hence, a polygon is a closed curve (figure) formed by the line segments such that – 

1. No line segments intersect except at their endpoints.
2. No two line segments with a common endpoint are coincident.

In other words, a closed figure formed a three or more line segment is called a polygon.

Triangles, quadrilaterals, pentagons, hexagons, octagons are all examples of polygons. The name of the shape tells us the number of sides it has. For example, a triangle has 3 sides, as “Tri” means 3. Similarly, the Pentagon has 5 sides as “Penta” means 5.  A regular polygon is a polygon whose all sides and all angles are equal. Let us see how to calculate the area of some polygons. 

Polygons are classified according to the number of sides as follows – 

Number of Sides or Vertices	Name of the Polygon
3	Triangle
4	Quadrilateral
5	Pentagon
6	Hexagon
7	Heptagon
8	Octagon
9	Nonagon
10	Decagon

How to find the area of a polygon having n sides?

We know that area the amount of space covered by a flat surface or piece of land or an object is called its area. Similarly, the area of a polygon is the total space or region bound by the sides of a polygon.

For the regular polygons, it is easy to find the area for them, since the dimensions are definite and known to us. For example, the area of a rectangle can be easily determined if we know the length and breadth of the rectangle. Similarly, the area of the square can be obtained even if we know one of its sides as all its sides are equal. Some regular polygons such as rectangles, squares, trapeziums, parallelograms etc. have a pre-defined formula that can be used to determine their areas. But, how can we find the area of a polygon having “ n “ sides?

Now, in order to find the area of a polygon that has not a regular defined shape, we need to first split it into triangles, squares, trapezium, etc. The purpose is to visualize the given figure as a combination of geometries for which we already know how to calculate the area. Another way of obtaining the area of a polygon is by using the common formula that has been derived for this purpose.

The area of a regular polygon with “ n “ sides and length “ a “ is given by

Area of a polygon with “ n “ sides and “ a “ length = $\frac{n}{4}$x a² x cotcot $\frac{\pi}{n}$  

How to find the area of a polygon using the polygon calculator?

We now know the formula for finding the area of a polygon if we know one of its sides as well the number of sides the polygon has. Let us now check how to perform the same operation using the polygon calculator.

The following steps will be performed for finding the area of a polygon using the polygon calculator – 

Step 1 – The first step is to select the “ solve for “ option in the polygon calculator. Since we need to find the area we will select the area option from the drop-down box of the “ solve for “ section. Below is a snapshot of how the selection would look like when we select the area from the drop-down options – 

Step 2 – Now that we have selected what need to solve, the next step is to enter the information that is available to us. If we look at the formula closely, there are two variables in the formula for finding the area of a polygon if we know one of its sides as well the number of sides the polygon has. These two values are “ n – the number of sides of the polygon “ and “ a – the length of one side. Therefore, in this step we shall select the option “ number of sides and outer a “ from the given section of the polygon calculator. Below is a snapshot of how the selection would look like when we select option “ number of sides and outer a “ from the drop-down options – 

Step 3 – As soon as we select the “ number of sides and outer a “ from the drop-down options, we will notice two boxes where we need to enter these values. Let us take an example. Suppose we wish to find the area of a polygon having 8 sides where each side is of the length 6 cm. If we would have used the formula for finding the area of the polygon, it would have been – 

 Area of a polygon with “ n “ sides and “ a “ length = $\frac{n}{4}$x a2 x cotcot $\frac{\pi}{n}$  

Here, n = 8 and a = 6 Therefore, we have

Area of the polygon =  $\frac{6}{4}$x 6² x cotcot $\frac{\pi}{8}$

⇒ Area of the polygon =  $\frac{3}{2}$ x 36 x cotcot $\frac{\pi}{8}$ = 173.82 sq. cm

Now, let us perform the same operation using the polygon calculator. 

Therefore, in this step, we shall enter the values of “ n “ and “ a “ in the boxes that have been provided post our selection in the previous step. Below is a snapshot of how the selection would look like when we will enter the values of “ number of sides and outer a “ from the drop-down options – 

Step 4 – Now that we have entered both what we wish to solve for and what has been given to us, we need to find the area of the polygon. For this purpose, we just need to click on the “ calculate “ button. As soon as we will click on this button, we can see the result obtained on the right-hand side of the values that we had entered in the previous steps. Below is a snapshot of how the selection would look like when we will click on the “ calculate “ button –

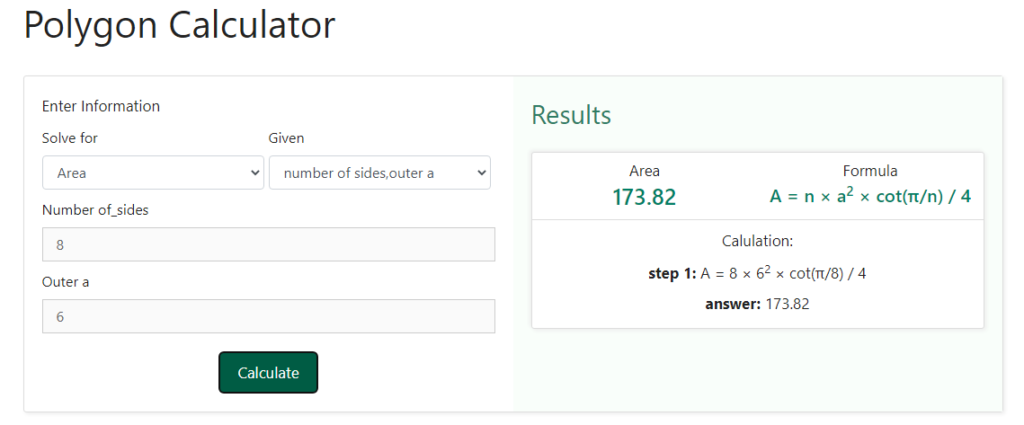
We can clearly see that the result obtained through the calculator as well the result obtained through the formula are the same. What’s more, the calculator also displays the formula as well as the steps involved in the calculation. The repeated use of this calculator allows you to not only check the results but also understand the formula and steps involved in finding the area of the polygon, thus allowing you to have a stronghold on the concept itself.