Octagon Calculator. Find the area, side a and perimeter of an Octagon with our free to use calculator. Fantastic math tool. Click below to utilise it right now.
What is an octagon?
We know that an octagon is a polygon formed with eight sides and eight angles. Also, in a regular octagon, the lengths of all the sides and the measurement of all the angles are equal.
How do we find the area of an octagon?
When we talk of the area of the octagon we mean to consider the space that is confined within the sides of the polygon. The area of an octagon is calculated by using the following formula –
Area of an octagon = 2s2 ( 1 + √2 )
where “ s “ is the side of a regular octagon.
Let us understand the formula using an example.
Example
Suppose, we wish to find the area of an octagon having a side of 2.3 cm
Solution
We have been given that we have an octagon that has a side of 2.3 cm. Now, we already know that the area of an octagon is given by Area of an octagon = 2s2 ( 1 + √2 ), where “ s “ is the side of a regular octagon.
If we substitute “ s” in the above equation by 2.3, which is the length of a side of our regular octagon, we will have,
Area of an octagon = 2s2 ( 1 + √2)
⇒ Area of an octagon =2 x ( 2.3 )2 ( 1 + √2)
Area of an octagon = 25.542 sq. cm
Therefore, the area of the octagon having a side of 2.3 cm will be 25.542 sq. cm = 25.54 sq. cm (approx.).
How can we use the octagon calculator to perform this operation? Let us find out.
How to use the octagon calculator to find the area of an octagon when we are given its side?
We know that Area of an octagon = 2s2 ( 1 + √2 ), where “ s “ is the side of a regular octagon.
Through the above formula we can see that if are given the side of a regular octagon, we can find its area.
Let us consider an example where we want to find the area of an octagon having a side of 4 cm. we shall now see how this operation can be performed using the octagon calculator. The following steps are to be followed for finding the area of an octagon –
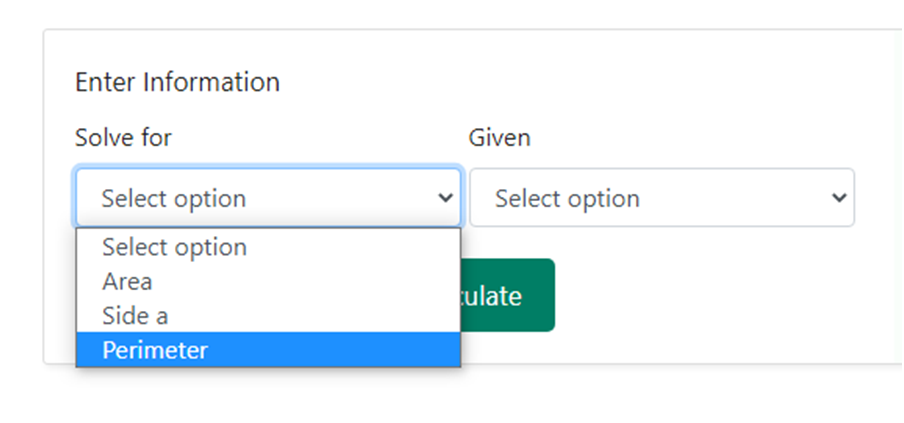
Step 1 – The first step is to choose the option of solving for “ area “ from the drop-down option given in the “ Enter Information “ section. Below is a snapshot of how the drop-down box would like upon choosing the area as selection –
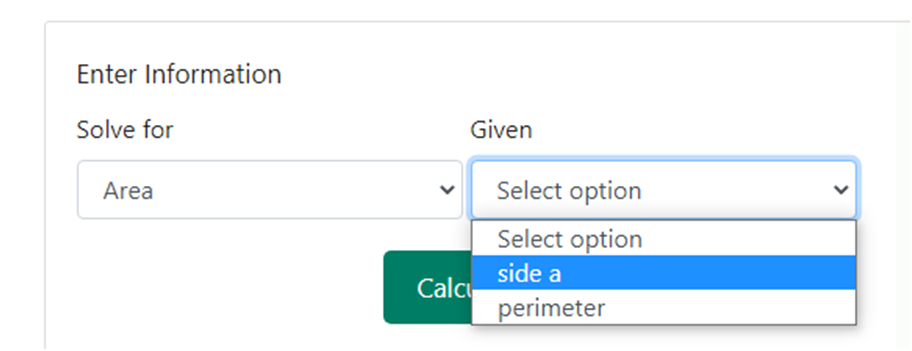
Step 2 – Once we have chosen “ Solving for the area “ of our option, the next side is to choose what is given to us. In the given section, we need to choose “ side a “ as the option as we are given with the side of the octagon. Below is a snapshot of how the drop-down box would like upon choosing side as selection –
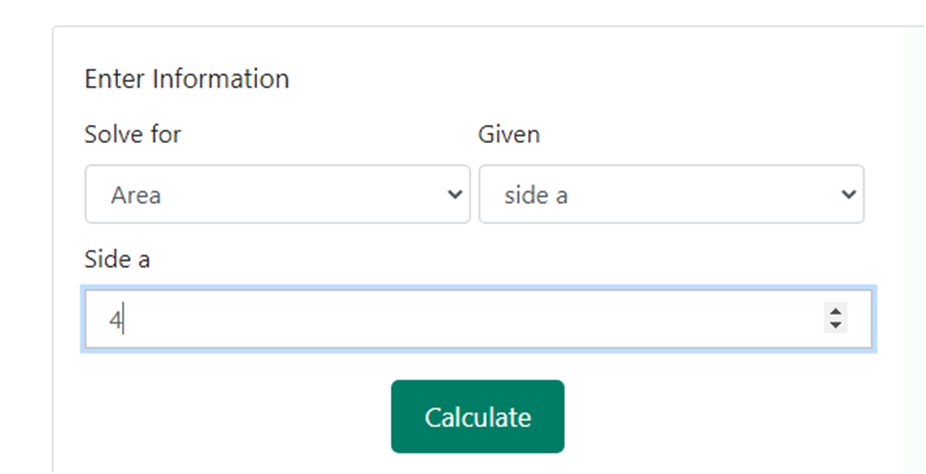
Step 3 – Now that we have chosen both what is required and what is given, we need to enter the value of the side that is given to us. As soon as we choose a side as the option in the previous step, another box crops up that asks us to enter the value of the side of the octagon. Since we have been given the side as 4 cm, we shall enter 4 in this box. Below is a snapshot of how the drop-down box would like upon having the requirement of entering the value of the side –
Step 4 – The last step is to click on the calculate button to obtain the value of the area. As soon as we will do that we shall have the results on the right hand side of the information that we entered in the above steps. Below is a snapshot of how the result would be displayed once we click on the calculate button.
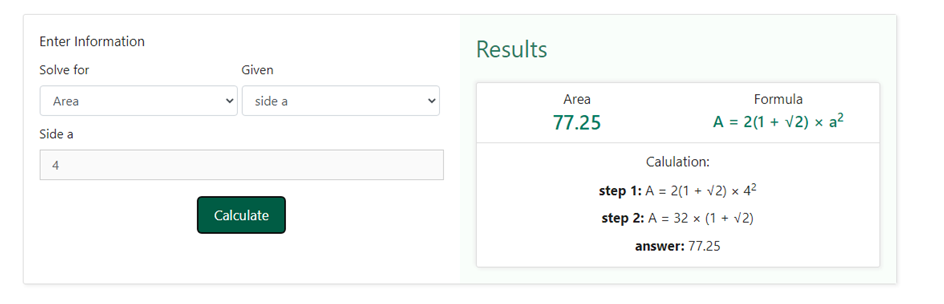
We can clearly see that only do we get the answer we also get to know the formula used as well as the steps involved in the calculation. This not only helps us to verify our answers but also helps us in having getting to learn more about the concepts related to the area of the circle and other dimensions related to it.
Can we find the area of an octagon using its perimeter? Let us find out.
How to find the area of an octagon when are given its perimeter?
In order to find the area of an octagon when are given its perimeter, we need to first understand the formula of the perimeter of the octagon.
The perimeter of an octagon = 8 x s, where, “ s “ is the side of a regular octagon.
Let us understand it using an example.
Suppose we have an octagon having the side 4 cm. what would be its perimeter?
The perimeter of the octagon would be given by 6 x Side = 8 x 4 = 32 cm.
Now, let us see how we can use this formula to find the area of an octagon.
We know that
Area of an octagon = 2s2 ( 1 + √2 ) ……………… ( 1 )
where “ s “ is the side of a regular octagon.
We also know that the Perimeter ( P ) of an octagon = 8 x s, where “ s “ is the side of a regular octagon. This means that P = 8s ⇒ s = $\frac{P}{8}$…………………….. ( 2 )
Substituting the value of s from ( 2 ) in equation ( 1 ) we get,
Area of a octagon = 2 x $\frac{P^2}{64}$ x ( 1 + √2 )
⇒ Area of an octagon = $\frac{P^2}{32}$ x ( 1 + √2 )
⇒ Area of an octagon =$\frac{P^2}{32}$ x ( 1 + √2 )which is our formula for finding the area of an octagon using its perimeter.
Let us understand it using an example.
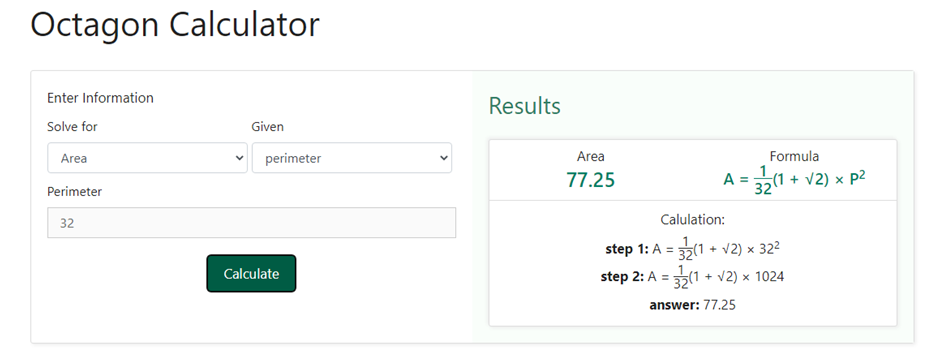
Suppose the perimeter of an octagon is 32 cm and we want to find its area. We will have,
Area of an octagon = $\frac{P^2}{32}$ x ( 1 + √2)
⇒ Area of an octagon = $\frac{32\: x\: 32}{32}$ x ( 1 + √2)= 77.248 sq. cm = 77.45 sq. cm ( approx.)
Let us see how to use the octagon calculator for finding the area using perimeter.
How to use the octagon calculator to find the area of an octagon when we are given its perimeter?
The steps required to find the area of the octagon when we have been given the perimeter are the same as we performed above except for the fact that in step 2 we will choose perimeter in the given section in step 2.
Below is the snapshot that displays the input as well as the result we will receive after entering the given input –