Circumference Calculator

What is a circle?

A circle is the set of all those points in a plane whose distance from the fixed point remains constant. The fixed point is called the centre of the circle and the constant distance is known as the radius of the circle. The line segment passing through the centre of a circle and having its end points on the circle is called the diameter of the circle. 

What is the circumference of a circle?

The perimeter of a circle is called the circumference of the circle. The ratio of the circumference of a circle and its diameter is always constant. In other words, the circumference of the circle or perimeter of the circle is the measurement of the boundary of the circle.

How to find the circumference of a circle?

If we have a circle, having radius “ r “, we will use the following formula for finding the circumference of a circle – 

Circumference of a circle = 2 π r where “ r” is the radius of the circle and π is the constant having the value $\frac{22}{7}$ or3.14 ( approx. ). Let us understand dit using an example.

 Suppose we have a circle, having a radius of 14 cm. What would be the circumference of this circle? Let us use the formula that we have stated above – 

Circumference of a circle = 2 π r = 2 x $\frac{22}{7}$ x 14  =  22 x 4 = 88 cm

How to find the area of a circle?

The area of a circle having a radius ‘r’ (The distance from the centre to a point on the boundary) is given by πr² where π = $\frac{22}{7}$ or 3.14 (approx.)

Suppose we are required to find the area of a circle having a diameter of 4.2 cm.

Here diameter (d) = 4.2 cm

By the relation between radius and diameter, we have, r = $\frac{d}{2}$

Hence r = $\frac{4.2}{2}$ = 2.1 cm

Now, area of this circle = = πr² = $\frac{22}{7}$ x 4.2 x 4.2 = 55.44 cm²

Using circumference to find the diameter and area of a circle

If we know the circumference of a circle, can we find its diameter and its area? Let us find out. We know that diameter of a circle is twice its radius. This means that if  “ r “ is the radius of the circle and “ d “ is the diameter of the circle, then, d = 2 r

Also, we now know that  

Circumference of a circle = 2 π r

Therefore, we can also define the formula for finding the circumference of the circle as 

Circumference of a circle = π d

From the above formula, we can see that if we know the circumference of the circle, we can find its diameter. Let us take an example. 

Suppose we have a circle whose circumference is 44 cm. What would be its diameter?

We know that – 

Circumference of a circle = π d

⇒ 44 = $\frac{22}{7}$ x d

⇒ d = $\frac{44 x 7}{22}$ = 14 cm

Hence, the diameter of a circle having a circumference of 44 cm is 14 cm.

Now, let us see how we can find the area of a circle if we know its circumference. Let us the same example that we have discussed above where the circumference of the circle was 44 cm. What will be the area of this circle?

We know that –

Circumference of a circle = 2 π r

⇒ 44 = 2 x  $\frac{22}{7}$ x r

⇒ r = $\frac{44 x 7}{2 x 22}$ = 7 cm

Now, we also know that,

Area of a circle  = π r²

Therefore, 

Area of a circle  =  $\frac{22}{7}$ x 7 x 7 = 154 sq. cm

How to use the circumference calculator to find the circumference of a circle?

It is quite simple to use the circumference calculator to find the circumference of a circle. Below are the steps that should be followed for this purpose

Step 1 – This calculator works on finding the circumference of a circle if we know its radius. Below is the snapshot of how the display would be like as soon as we land on the circumference calculator page – 

Step 2 –  Now, as we can see we are required to enter the radius of the circle. Let us take, for example, the radius as 2.1 cm. If we want to find the circumference of a circle, having a radius of 2.1 cm, we will have to enter 2.1 in the box below the “ Enter radius “ option of the calculator. Below is the snapshot providing detail of how the radius will be entered –

Step 3 – Now, that we have entered the radius of the circle, no further information is required to provide to the calculator. Therefore, the next is to calculate the circumference of the circle. For this purpose, we just need to click on the “ calculate “ button. As soon as we will click on this button, we can see the result obtained on the right-hand side of the values that we had entered in the previous steps. Below is a snapshot of how the selection would look like when we will click on the “ calculate “ button – 

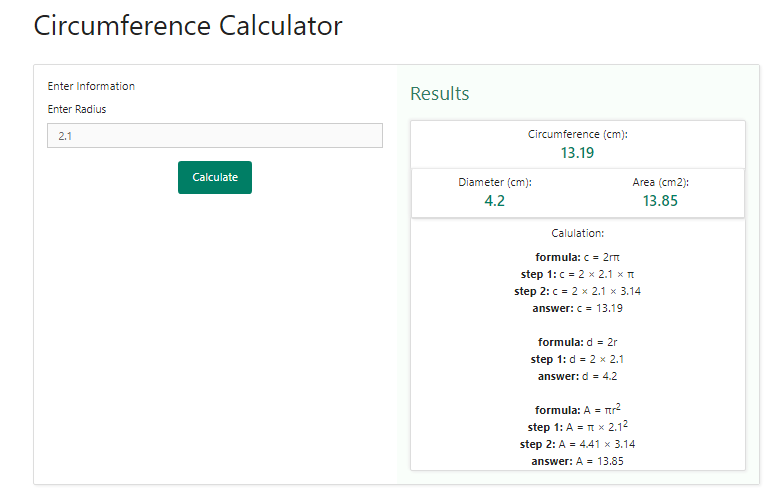
Let us check what all information and calculation has been provided to us the circumference calculator –

Circumference – The first information available is the circumference, which is 13.19 cm. 

Diameter –  The next information that has been provided through this calculator is the diameter which, for this example is 4.2 cm.

Area – The last information that has been provided through this calculator is the area of the circle, which, for this example is 13.85 sq. cm

The detailed explanation and usage of the relevant formula have been made available in the calculation section for all the three components, i.e. circumference, diameter and the area of the circle.  Therefore, we can clearly see that only do we get the answer we also get to know the formula used as well as the steps involved in the calculation. This not only helps us to verify our answers but also helps us in having getting to learn more about the concepts related to the circumference of the circle and other dimensions related to it.