What is Division?
Division is the equal sharing of a given quantity. For example, Alice wants to share 6 bananas equally with her friend Rose. So, she gives 3 of her bananas to Rose and she is also left with 3 bananas. This means that when we divide 6 by 2 we get 3. Mathematically, we can write this as 6 ÷ 2 = 3
Symbol for Division
In mathematics, there is a symbol for every operation. The symbol for division is (÷). Other than the forward-slash (/) is also used to denote the division of two numbers, where, the dividend comes before the slash and the divisor after it. For instance, if we wish to write 15 is being divided by 3, we can write it as 15 ÷ 3 or 15 / 3. Both mean the same.
Important terms in Division
The number that is to be divided is called the Dividend. Here, 6 is the dividend.
The number by which the dividend is being divided is called the Divisor.
The result obtained by the process of division is called the Quotient.
The number that is left over after finding the quotient is called the Remainder.
Let us understand these by an example.
Suppose, we have a pack of 65 chocolates and we want to divide them equally among 7 children while keeping the remaining chocolates with us. How many chocolates does each child get and how many chocolates are we left with after dividing these chocolates?
Using multiplication tables, we have 7 x 9 = 63
Therefore, 7 x 9 + 2 = 65
This means that the quotient when 65 is divided by 7 will be 9 and the remainder will be 2.
As per the definition of the four terms of division, we have
Divisor = 7
Dividend = 65
Quotient = 9
Remainder = 2
Remember: The remainder is always smaller than the divisor.
Formula for Division
There are four important terms in the division, namely, divisor, dividend, quotient, and the remainder. The formula for divisor constitutes all of these four terms. In fact, it is the relationship of these four terms among each that defines the formula for division. If we multiply the divisor with the quotient and add the result to the remainder, the result that we get is the dividend. This means,
Dividend = Divisor x Quotient + Remainder
Long Division
While it is quick and easy to divide a one-digit number, there are certain steps involved for larger numbers. This is called long division. Let us understand these steps using some examples. The steps involved for dividing a number by another depend on the digits of the dividend and the divisor. Let us understand these using some examples.
Suppose we wish to divide 78 by 6.
Compare the first digits of both the dividend and the divisor. The digit of the dividend is greater than that of the divisor. Therefore, in cases where the first digit of the dividend is equal to or greater than the divisor, the following steps should be followed –
Since 7 > 6 we can easily divide it by 6 leaving the remainder 1.
On subtracting 6 from 7 we get the remainder as 1.
Now, consider the second digit of the dividend which is 8. Combining 1 with 8 we get 18.
Now divide 18 by 6 and we get 3 as the quotient, leaving the remainder as 0 as 6 fully divides 18.
Therefore, 78 ÷ 6 = 13
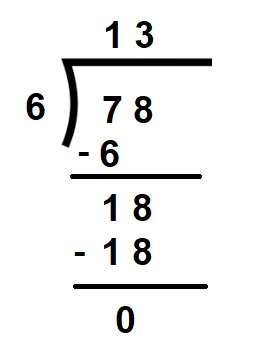
Now let us consider a case where the first digit of the dividend is less than that of the divisors. Suppose, we wish to divide 426 by 8
Now, we know that 4 < 8. Therefore, we will have to consider the first two digits of the dividend to divide by 8 in the first step.
We, therefore, take the first two digits, i.e. 42, and divide them by 8. We get 5 as the quotient and 2 as the remainder.
Next, we take consider the digit of the dividend, i,e, 6. Combing 2 with 6 we get the number 26.
Now, we divide 26 by 8 in which we get 3 as the quotient and 2 as the remainder.
Hence 426 ÷ 8 = 53, remainder = 2
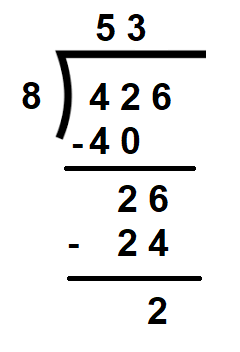
How to use the remainder calculator for dividing numbers?
Using the average calculator is quite simple. We just need to enter the divisor and the dividend and we get our result. The following steps are required to be followed for this purpose –
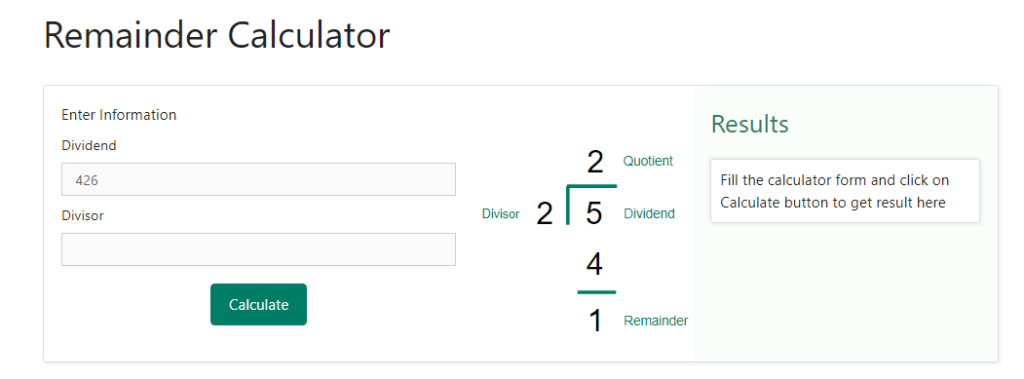
Step 1 – The first step is to enter the dividend as the input for the calculator. Recall that dividend is the number that is to be divided. Let us for example, attempt to divide 426 by 8. In this case, 426 will be the dividend. So, we shall enter 426 as the input for the calculator. Below is the snapshot providing detail of how the dividend will be entered –
Step 2 – Once we have entered the dividend, the next step is to enter the divisor. Recall that divisor is the number by which the dividend is being divided. Since we are dividing 426 by 8, therefore 8 is the dividend. So, we will enter 8 as the input for the calculator. Below is the snapshot providing detail of how the divisor will be entered –
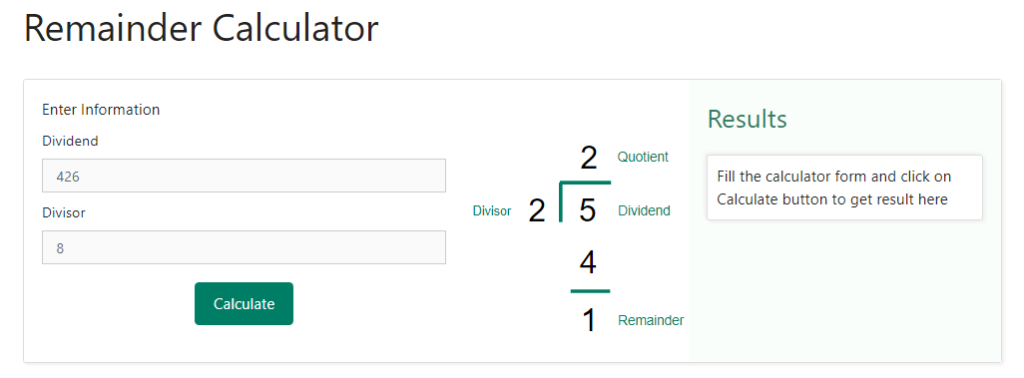
Step 3 – In the above two steps, we have entered the required information for the calculator to obtain the result when 426 is divided by 8. For this purpose, we just need to click on the “ calculate “ button. As soon as we will click on this button, we can see the result obtained on the right-hand side of the values that we had entered in the previous steps. Below is a snapshot of how the selection would look like when we will click on the “ calculate “ button
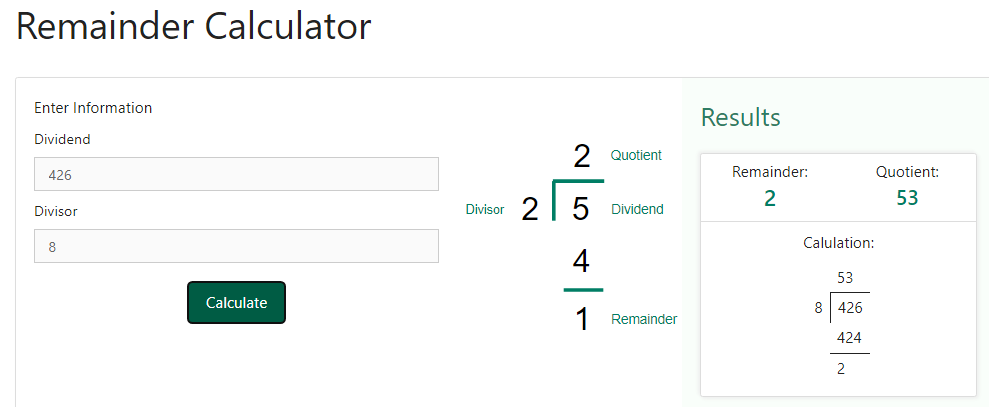
We had performed this division using the long division method above and we have now performed it using the calculator. Let us compare both the results. We can see that in both case, we obtained 53 as the quotient and 2 as the remainder. Moreover, the elaboration of the steps involved is also the same. Thus, we can clearly see that only do we get the answer we also get to know the formula used as well as the steps involved in the calculation. This not only helps us to verify our answers but also helps us in having getting to learn more about the concepts related to the area of the circle and other dimensions related to it.