What is a right angled triangle?
A triangle is said to be a right angled triangle if one of the angles of the triangle is a right angle, i.e. 90o. Suppose, we have a triangle, ABC where △ABC = 90o. Then such a triangle is called a right angled triangle which would be of a shape similar to the below figure.
What is Pythagorean Theorem?
Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides“. Suppose we have a triangle, having the sides a, b and c as shown below –

In the above triangle, the sides of the triangle are named as –
a = Perpendicular to the Base
b = Base of the right angled triangle
c – Hypotenuse of the right angled triangle
It is important to note here that the hypotenuse is the longest side, as it is opposite to the right angle formed in the triangle.
Now, the Pythagorean theorem states that if “ b “ is the base of the triangle, “ a “ is the perpendicular to the base of the triangle and “ c “ is the hypotenuse of the right angled triangle, then –
( Base ) 2 + ( Perpendicular ) 2 = ( Hypotenuse ) 2
⇒ a 2 + b 2 = c 2
Let us understand it using an example.
Example
The hypotenuse of a right angle triangle is 15 cm and the base of the triangle is 12 cm. Determine the perpendicular of the triangle.
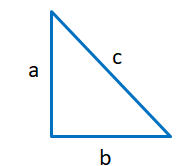
Solution
Use the Pythagorean Theorem:
In a right angled triangle ABC
c2=a2+b2 ……………………………….. (i)
where:
“c” is the hypotenuse, “b” is the base and “a” is the perpendicular.
We have been given that,
c = 15 cm
b = 12 cm
Substituting the values and b and c in the equation (i), we have,
(15)2 = (12)2 + a2
225 = 144 + + a2
a2 = 225 – 144 = 81
Hence, a = 9
Therefore, the perpendicular of the triangle is 9 cm.
How to use the Pythagorean calculator to find the sides of a right angled triangle?
Finding the sides of a triangle using our Pythagorean calculator is quite simple. You need to first select a square from the drop-down options given in the calculator section and then select the area from the drop-down option in the solve for the section as shown below –
We now know the formula for finding one of the sides of a right angled triangle is by using the Pythagoras theorem. If we know the other two sides we can find the third side of the right angled triangle. Let us now check how to perform the same operation using the Pythagorean calculator.
The following steps will be performed for finding the sides of a triangle using our Pythagorean calculator –
Step 1 – The first step is to select the “ solve for “ option in the Pythagorean calculator. Since we need to find one of three sides, be it the base, the perpendicular and the hypotenuse, we will select one of them from the drop-down box of the “ solve for “ section. Below is a snapshot of how the selection would look like when we select what we want to solve for from the drop-down options –
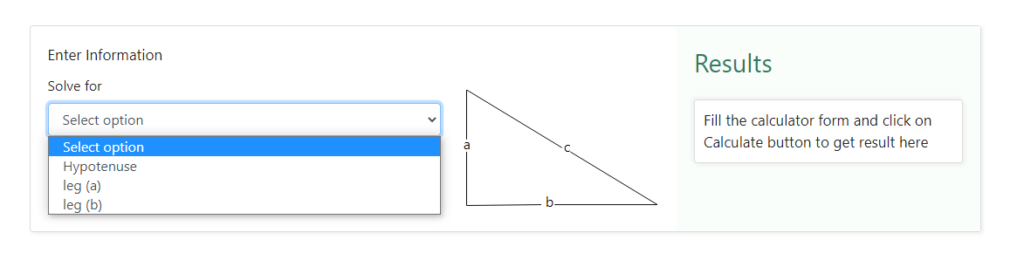
Here the terms “ a “ and d” leg b “ refer to the base and the hypotenuse of the right angled triangle.
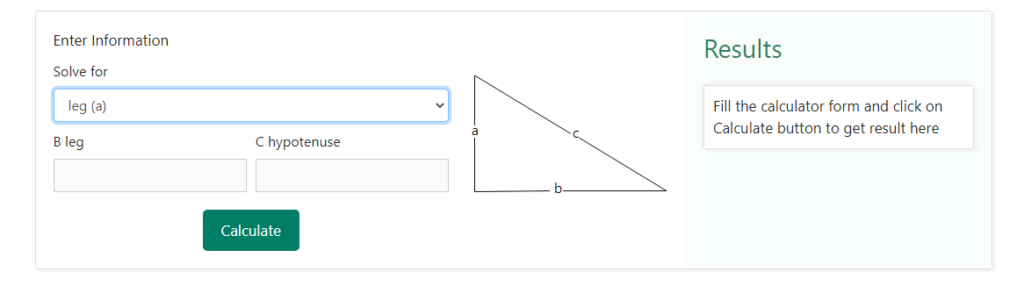
Step 2 – Now that we have selected what need to solve, the next step is to enter the information that is available to us. If we look at the formula closely, there are three variables in the formula, base, perpendicular and the hypotenuse. Suppose we want to find the base of the triangle and we have with us the values of the perpendicular and the hypotenuse. Therefore, in the previous step, we will select leg a or leg as the requirement to solve. Now, as soon as we select, suppose leg a, we will see that two boxes are prompted where we are required to enter the values of the perpendicular and the hypotenuse. Below is a snapshot of how the selection would look like when we select option “ leg a “ in the previous step and are now required to enter the perpendicular and the hypotenuse that have been given to us.
Step 3 – Now that we have been asked to enter the values of the perpendicular and the base, we shall enter them in the boxes provided. Suppose we have the perpendicular as 21 and the hypotenuse as 29 cm. If we would have used the Pythagoras formula for finding the base of the triangle, it would have been –
( Base ) 2 + ( Perpendicular ) 2 = ( Hypotenuse ) 2
⇒( Base ) 2 + 21 2 = 29 2
⇒( Base ) 2 + 441 = 841
⇒( Base ) 2 = 841 – 441
⇒( Base ) 2 = 400
⇒ Base = 20 cm
Now, let us perform the same operation using the Pythagorean calculator.
Therefore, in this step, we shall enter the values of “ leg b “ and “ hypotenuse “ in the boxes that have been provided post our selection in the previous step. Below is a snapshot of how the selection would look like when we will enter the values of “ leg b “ and “ hypotenuse “ from the drop-down options –

Step 4 – Now that we have entered both what we wish to solve for and what has been given to us, we need to find the base of the triangle. For this purpose, we just need to click on the “ calculate “ button. As soon as we will click on this button, we can see the result obtained on the right-hand side of the values that we had entered in the previous steps. Below is a snapshot of how the selection would look like when we will click on the “ calculate “ button
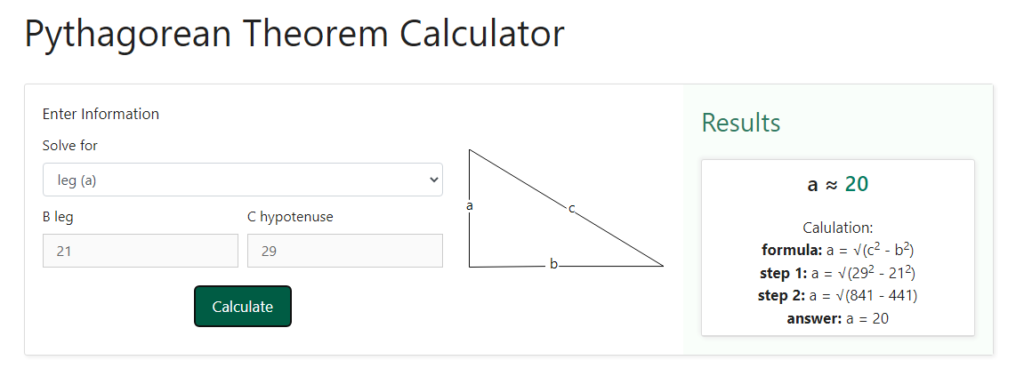
We can clearly see that the result obtained through the calculator as well the result obtained through the formula are the same. What’s more, the calculator also displays the formula as well as the steps involved in the calculation. The repeated use of this calculator allows you to not only check the results but also understand the formula and steps involved in finding the sides of a right angled triangle, thus allowing you to have a stronghold on the concept itself.