LCM Calculator

What is LCM?

The Least Common Multiple ( L C M ) of two or more numbers is defined as the smallest number ( other than zero ) that is a multiple of those numbers. In other words, the least common multiple of two or more numbers is the smallest number which is divisible by all the given numbers. This means that there cannot be a number divisible by the given numbers and smaller than the least common multiple.

Let us understand this through an example.

Suppose we have two numbers, 8 and 12.

Let us check the multiples of these two numbers. We have,

Multiples of 8 = 8, 16, 24, 32, 40 , 48, 56, 64, 72 and so on…..

Multiples of 12 = 12, 24, 48, 60, 72 and so on …………

From above we can see that the common multipleS of 8 and 12 are 24, 48, 72 and so on. Among these 24 is the least common multiple of these two numbers. Therefore, 12 is the least common multiple or L C M of 8 and 12.

How to Find a Least Common Multiple ( L C M ) ?

There are two major methods using which we can find the L C M of two or more numbers. These methods are – 

1. Prime Factorisation Method
2. Common Division Method

Let us discuss these methods one by one.

Prime Factorisation Method

As the name suggests, the prime factorisation method involves finding the prime factors of the given numbers and then computing the least common multiple ( L C M ). In this method, the following steps are used to find the L C M  – 

1. Obtain the given numbers.
2. Find the prime factors of each number. 
3. Expand each number as a product of its prime factors
4. Find the product of all different prime factors with the highest power in the prime factorisation of each number.
5. The number obtained in the above step is the required L C M of the given numbers.

Example

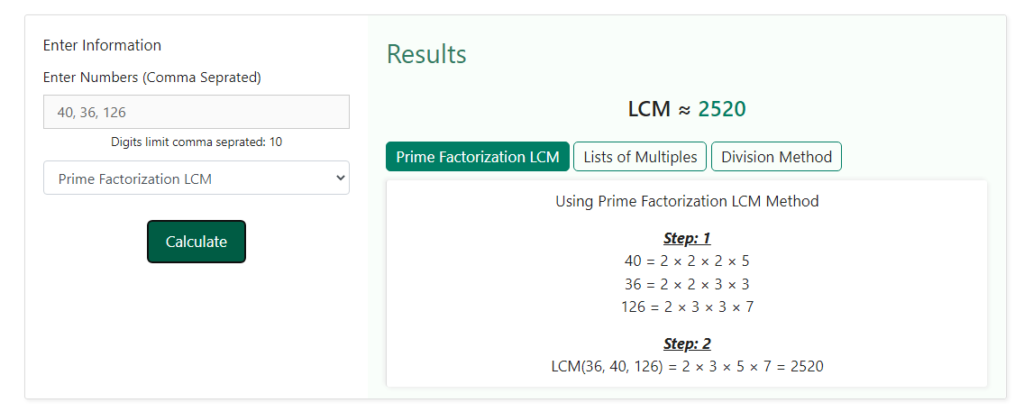
Find the L C M of 40, 36 and 126 using the prime factorisation method.

Solution

We have been given the numbers 40, 36 and 126 and we are required to find the L C M of these numbers. Going by the above steps let us first find the prime factors of each of the given numbers. We have,

Prime factors of 40 are – 

40 = 2 x 2 x 2 x 5

Prime factors of 36 are – 

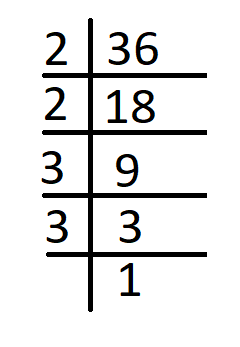
36 = 2 x 2 x 3 x 3

Prime factors of 126 are – 

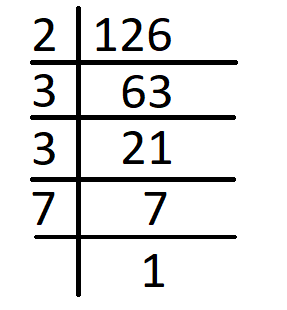
126 = 2 x 3 x 3 x 7

We can see in the above prime factorisations of the above numbers, the number 2 appears a maximum of three times, which is the case in the number 40. Similarly, the number 3 appears as a factor for the maximum number of 2 times, which is the case in 36 and 126. The prime factors 5 and 7 occur only in 40 and 126 respectively. Therefore, the required L C M of the numbers, 40, 36 and 126 will be 

L C M of 40, 36 and 126 = 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520

Hence, L C M of 40, 36 and 126 = 2520

Common Division Method

The following steps are followed to find the L C M of two or more numbers using the common division method – 

1. Obtain the given numbers.
2. Arrange the given numbers in a row separated by commas.
3. Obtain a number that divides exactly at least two of the given numbers.
4. Divide the numbers which are divisible by the number chosen in the above step and write the quotients just below them. Carry forward the numbers which are not divisible.
5. Repeat the above steps till no two of the given numbers are divisible by the same number.
6. Find the product of the divisors and the undivided numbers to get the required L C M of the given numbers.

Let us understand the above steps using an example.

Example

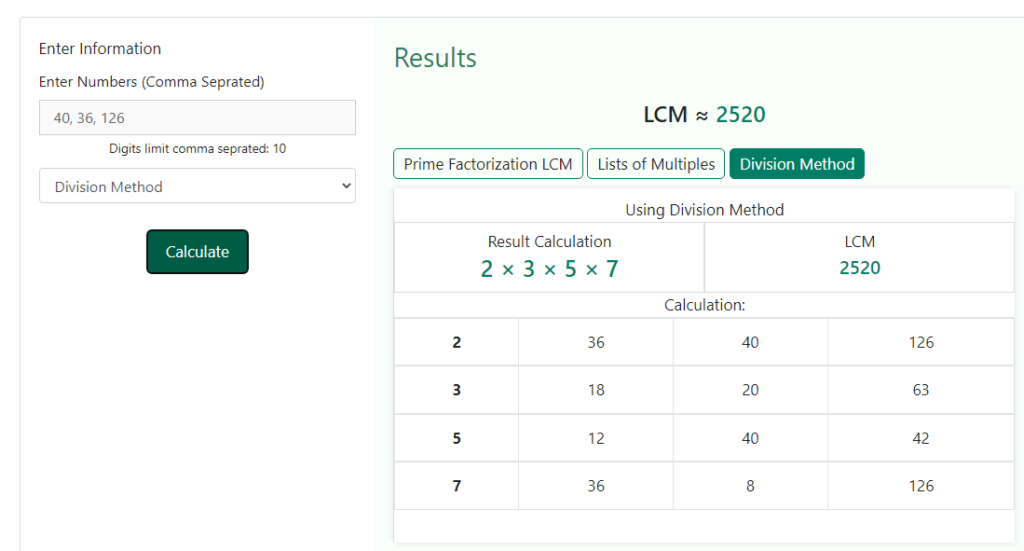
Find the L C M of 624 and 936 using the common division method.

Solution

We have been given the numbers 624 and 936 and we are required to find the L C M using 624 and 936.

We have,

From the above common division we have,

L C M of the numbers 624 and 936 = 2 x 2 x 2 x 3 x 13 x 2 x 3 = 1872

Hence, L C M of the numbers 624 and 936 = 1872

How to find LCM using the LCM calculator?

The following steps will be performed for finding the LCM of a given set of numbers using the LCM calculator – 

Step 1 – The first step is to enter the numbers whose LCM is required to be obtained. Below is the snapshot of the LCM calculator where we need to enter the values – 

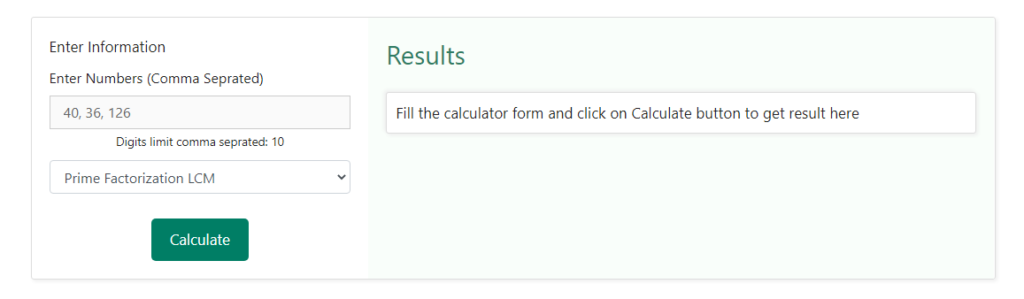
Step 2 – Suppose we take the example, we discussed above where we calculated the LCM of 40, 36 and 126. Hence, we will enter the values like 40, 36, 126. Below is the snapshot of how these values will be entered – 

Step 3 – In the next step, we are required to choose the method through which we need the LCM to be calculated. The available options are – Prime factorisation, Listing the multiples and Division method.  Below is the snapshot of how the selection needs to be made through the drop-down options – 

Step 4 – Suppose e choose the prime factorisation method. We will thus select this option from the drop-down options –

Step 5 – Now that we have entered the values whose LCM needs to be calculated and the method through which it is needed to be one, we just need to find LCM. For this purpose, we just need to click on the “ calculate “ button. As soon as we will click on this button, we can see the result obtained on the right-hand side of the values that we had entered in the previous steps. Below is a snapshot of how the selection would look like when we will click on the “ calculate “ button

If we would have chosen the division method the result would have been as shown below – 

We can clearly see that the result obtained through the calculator as well the result obtained through the formula are the same. What’s more, the calculator also displays the formula as well as the steps involved in the calculation. The repeated use of this calculator allows you to not only check the results but also understand the formula and steps involved in finding the sides of a right angled triangle, thus allowing you to have a stronghold on the concept itself.