Standard Deviation Calculator

What is Variance?

The variance of a variable X is the arithmetic mean of the squares of all derivatives of X from the arithmetic mean of the observations and is denoted by Var ( X ) or σ ². In other words, The variance measures the average degree to which each point differs from the mean—the average of all data points. Let us now learn about some properties of variance.

What is Standard Deviation?

The positive square root of the variance of a variate X is known as its standard deviation and is denoted by σ. In other words, Standard deviation looks at how to spread out a group of numbers is from the mean, by looking at the square root of the variance.

Thus,

Standard Deviation = $\sqrt{Var ( X )}$

It is important to note here that, Standard deviation and variance both are measures that tell how spread out the numbers is. While variance gives us a rough idea of spread, the standard deviation is more concrete, giving us the exact distances from the mean.

Variance and Standard Deviation of Individual Observations

If x1, x₂, x₃, ……, x_n are n values of a variable X, then,

Variance ( X ) = $\frac{\sum_{i=1}^{n}(x_1-\overline{x})^2}{2}$

Also,

Variance ( X ) = [$\frac{1}{N} \sum_{i=1}^{n}f_i x_i$ ] ²

Another formula for variance is given by

Variance ( X ) = $\frac{1}{N}$ [ $\sum{f_i d_i^2}$ ] – [$\frac{1}{N} \sum_{i=1}^{n}f_i d_i$ ] ²

In the case of individual observations, variance and standard deviation may be computed by applying any of the above three formulas. We can now define the algorithm for finding the variance when deviations are taken from the actual mean. The algorithm is as follows – 

Algorithm for finding the variance when deviations are taken from the actual mean

1. Compute the mean $\overline{X}$ of the given observations x₁, x₂, x₃, x₄, ……. x_n.
2. Take the deviations of the observations from the mean i.e. to find xi – $\overline{X}$ ; I = 1, 2, 3, ………, n.
3. Square the deviations obtained in the above step and obtain the sum 
   $\frac{\sum_{i=1}^{n}(x_1-\overline{x})^2}{2}$ .
4. Divide the sum  $\frac{\sum_{i=1}^{n}(x_1-\overline{x})^2}{2}$ obtained in the above step by n. this gives us the variance of X.

Let us understand this through an example.

Example Compute the variance and the standard deviation of the following observations of the following data – 

  65, 68, 58, 44, 48, 45, 60, 62, 60, 50

Solution We have been given the data – 65, 68, 58, 44, 48, 45, 60, 62, 60, 50. We are required to find the variance and the standard deviation of the given data. 

Let $\overline{X}$ be the mean of the given set of observations. Then,

$\overline{X}$ = $\frac{65+ 68+ 58+  44 + 48+  45 + 60+  62+  60 + 50}{10}$ = $\frac{560}{10}$ = 56

Let us now compute the variance of the given data

xi	xi – $\overline{X}$ = xi – 56	(xi – $\overline{X}$ ) 2
65 58 68 44 48 45 60 62 60 50	9 2 12 -12 -8 -11 4 6 4 -6	81 4 144 144 64 121 16 36 16 36
		(xi – $\overline{X}$) 2 = 662

We can see that number of observations is 10. Therefore, n = 10

Variance = $\frac{\sum_{i=1}^{n}(x_1-\overline{x})^2}{n}$ = $\frac{662}{10}$ = 66.2

Hence, Standard Deviation = $\sqrt{Variance}$ = $\sqrt{66.2}$ = 8.13

Therefore, for the given set of observations,

Variance = 66.2 and Standard Deviation = 8.13

How to find variance and standard variance using the standard deviation calculator?

Finding the variance and the standard deviation using our standard deviation calculator is quite simple. You just need to enter the values for which the variance and the standard deviation needs to be calculated. Below are the steps to be followed for this purpose – 

Step 1 –  The first step is to locate the box where we need to enter the values for which we wish to find the variance and the standard deviation. These values should be separated by commas. Below is the snapshot of the option that would be displayed for this purpose – 

Step 2 – The next step is to enter the values. Let us for example, consider the example that we discussed above where we had the values  65, 68, 58, 44, 48, 45, 60, 62, 60, 50 for which we wanted to compute the variance and the standard deviation. Let us enter the same values in the standard deviation calculator. Below is the snapshot of how the values would be entered – 

Step 3 –  Now that we have entered the values, the next step is to compute the variance and the standard variation. For this purpose, we just need to click on the “ calculate “ button. As soon as we will click on this button, we can see the result obtained on the right-hand side of the values that we had entered in the previous steps. Below is a snapshot of how the selection would look like when we will click on the “ calculate “ button

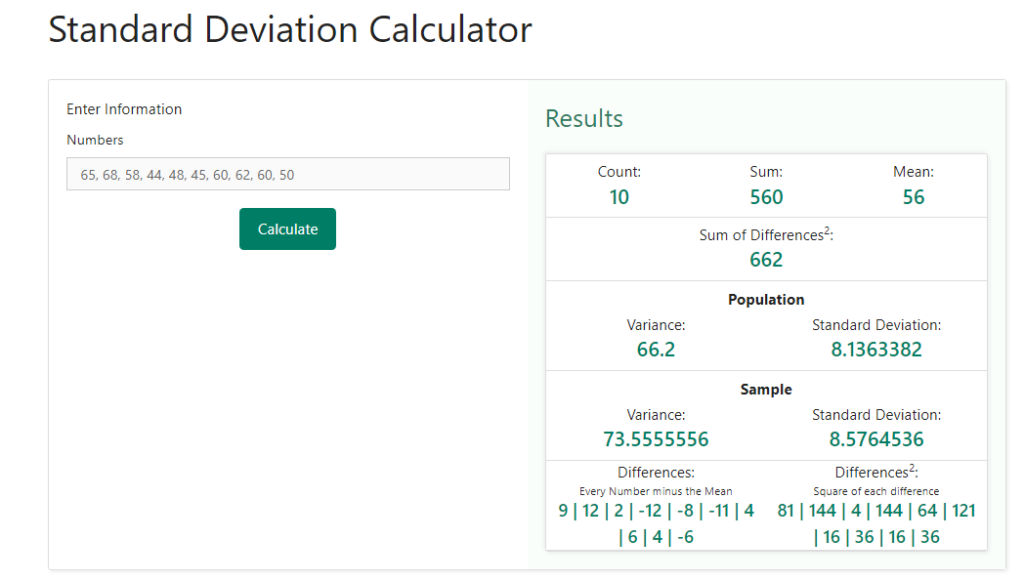
Let us see in detail the results that have been provided to us. 

Count – This is the number of values that we provided for computation. 

Sum – This is the sum of the values which we provided for computation. 

Mean – This is the mean of the values which we provided for computation. Note that this value is the same as the one we had obtained in the form of $\overline{X}$ in the above example. 

Sum of differences – This is the value of (xi – $\overline{X}$ ) ² that we had computed when finding the variance and standard deviation.

The other terms are variance, standard deviation, difference etc. which are all the same as were computed when the same was computed using the formula. So, we can clearly see that the result obtained through the calculator as well the result obtained through the formula are the same. What’s more, the calculator also displays the formula as well as the steps involved in the calculation. The repeated use of this calculator allows you to not only check the results but also understand the formula and steps involved in finding the sides of a right angled triangle, thus allowing you to have a stronghold on the concept itself.