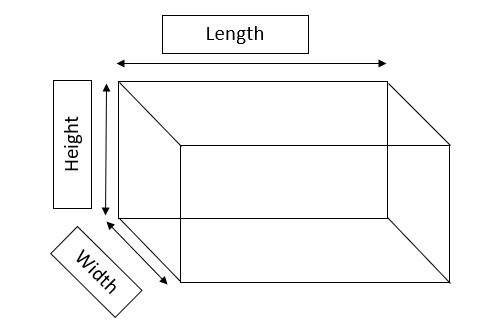
CFT is also known as cubic feet or ft3, a unit measurement of volume. This is the US customary unit of volume, used in the United States and the United Kingdom. Utilise our Cubic Feet calculator below across a unit choice of inches, yards, millimetres, centimetres, metres or feet.
 Calulation:
Calulation:
How to use the cubic feet calculator?
The followings steps should be used to use the cubic feet calculator –
- Fill the blanks of length, width and height
- Choose the unit of measure you are using ( in, ft, yd, mm, cm, m )
- Then you will know how many are the cubic inches ( in³ )
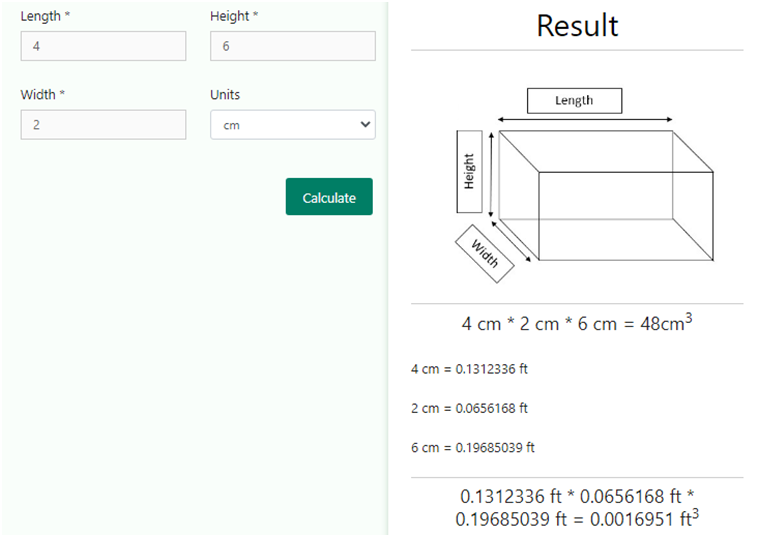
Let us consider an example. For instance, we wish to find the volume of a cuboid having length 4 cm, breadth 2 cm and height of 6 cm. now, if we go as per the formula, the volume will be
Volume of the cuboid = length x breadth x height = 4 cm x 2 cm x 6 cm = 48 cu. cm
Now, if we wish to convert the result in ft, we will have to use the relation,
1 cm = 0.0328084 ft.
Therefore, 4 cm = 4 x 0.0328084 ft. = 0.1312336 ft.
Similarly, 2 cm = 2 x 0.0328084 ft. = 0.0656168 ft. and height = 6 cm = 6 x 0.1312336 ft. = 0.19685039 ft.
Therefore, the volume in cu. ft. will be
Volume of cuboid = 0.1312336 ft. x 0.0656168 ft. x 0.19685039 ft.
⇒ Volume of cuboid = 0.0016951 cu. ft The same can be verified through the cubic feet calculator as shown below –
What are cubic feet?
Cubic feet as the name suggests is a unit of volume of a 3 dimensional shape. We know that 3 Dimensional shapes such as a cuboid have three dimensions, namely, length, breadth and height. Similarly, a cubic inch is a measure of volume that is equal to a cube with width; length and height are all 1 inch. We also know that
Volume of a cuboid = length x breadth x height unit3
This means that, if l is the length of a cuboid, b is the breadth and h is the height, then,
Volume of a cuboid = length x breadth x height = l x b x h unit3
This unit, if mentioned in feet. is unit as cubic feet. A Cubic foot is one of the units in which we can measure the volume of a 3 dimensional object.
We know that volume is a three-dimensional quantity. It is the amount of capacity/space a substance contains, or the space it can hold. How is volume measured in the various metrics? Let us find out.
Type of Metrics
We have different types of metrics depending upon the length of a 3 dimensional object. The system that defines these different metrics is known as the metric system. In other words, the metric system can be defined as a system of measurement that uses the litre, metre, and gram as base units of metric length (distance), capacity (volume), and weight (mass) respectively.
But for smaller quantities, we have other units such as centimetres, inches etc. So, what are these units and how are they related to each other.
The common metrics of length are –
- Kilometres, abbreviated as km
- Metres, abbreviated as m
- Centimetres, abbreviated as cm
- Inches, abbreviated as in
- Feet, abbreviated as ft
- Millimetres, abbreviated as mm
Let us now learn about the relationship between various metrics of length.
Conversion from One Metric to Another
The following are the relationships between various metrics of length –
- 1 yard = 91.44 centimetres = 0.9144 metre
- 1 foot = 30.48 centimetres = 0.3048 metre
- 1 inch = 2.54 centimetres = 0.0254 metre
- 1 meter = 100 centimetres
- 1 millimetre = 0.1 centimetres = 0.001 metre
Now, let us see how these units can be converted from one metric to another when in cubic form. below we have the cubic metre formula for different units
Length ( meters ) x width ( meters ) x height ( meters ) = cubic meters ( m³ )
Length ( c m) x width ( cm ) x height ( cm ) = cubic centimetres ( cm³ )
Length ( cm ) x width ( cm ) x height ( cm ) / 1,000,000 = cubic metres ( m³ )
Length ( mm ) x width ( mm ) x height ( mm ) = cubic millimetres ( mm³ )
Length ( mm ) x width ( mm ) x height ( mm ) / 1,000,000,000 = cubic meters ( m³ )
Length ( inches ) x width ( inches ) x height ( inches ) = cubic inches ( in³ )
Length ( inches ) x width ( inches ) x height ( inches ) / 61,023.8 = cubic meters ( m³ )
Length ( feet ) x width ( feet ) x height ( feet ) = cubic feet ( ft³ )
Length ( feet ) x width ( feet ) x height ( feet ) / 35.315 = cubic meters ( m³ ) The above stated relations between units can also be presented in the form of a table as –
Linear Measure
We start with 1 millimetre which we represent as 1 mm. Now,
| 1 centimetre ( 1 cm ) | = | 10 millimetre | = | 10 mm |
| 1 metre ( 1 m ) | = | 100 centimetre | = | 100 cm |
| 1 kilometre ( 1 km ) | = | 1000 metre | = | 1000 m |
| 1 inch ( 1 in ) | = | 25.4 millimetre | = | 25.4 mm |
| 1 foot ( 1 ft. ) | = | 12 inches ( 12 in ) | = | 0.3048 m |
| 1 yard ( 1 yd. ) | = | 3 feet ( 3 ft. ) | = | 0.9144 m |
| 1 mile | = | 1760 yards | = | 1.609 km |
Similarly, the chart for the conversion of cubic units can be presented as –
We start with 1 cubic centimetre which will be represented as cubic centimetres, cu. cm or cm3
| 1 cubic metre ( cu. m or m3 ) | = | 1, 000, 000 cm3 |
| 1 cubic inch | = | 16.4 cm3 |
| 1 cubic foot | = | 1728 cu. in = 0.0283 cu. m |
| 1 cubic yard | = | 27 cu. ft = 0.765 cu. m |
Where can it be used?
There can be wide applications of these metrics depending upon the object whose volume is being measured. For instance –
- The thickness of a credit card or a plastic identity card as well as their volumes can be measured in millimetre cubes or cubic millimetres ( cu. mm or mm3).
- The length of a fingernail or a mobile phone can be measured in centimetres. Therefore, their volumes as well can be measured in centimetres cubes or cubic centimetres ( cu. cm ).
- The capacity of a room can be measured in cubic metres.