Probability Calculator Find the probability of single, two and multiple events with our handy calculator. Fantastic math tool. Click below to utilise it right now.
| Probability of A occuring 5 time(s) | 0 |
| Probability of A NOT occuring | 0 |
| Probability of A occuring | 0 |
| Probability of B occuring 3 time(s) | 0 |
| Probability of B NOT occuring | 0 |
| Probability of B occuring | 0 |
| Probability of A occuring 5 times and B occuring 3 times | 0 |
| Probability of neither A nor B occuring | 0 |
| Probability of both A and B occuring | 0 |
| Probability of A occuring 5 times but not B | 0 |
| Probability of B occuring 3 times but not A | 0 |
| Probability of A occuring but not B | 0 |
| Probability of B occuring but not A | 0 |
| Probability of A NOT occuring: P(A') | 0 |
| Probability of B NOT occuring: P(B') | 0 |
| Probability of A and B both occuring: P(A∩B) | 0 |
| Probability that A or B or both occur: P(A∪B) | 0 |
| Probability that A or B occurs but NOT both: P(AΔB) | 0 |
| Probability of neither A nor B occuring: P((A∪B)') | 0 |
| Probability of A occuring but NOT B: | 0 |
| Probability of B occuring but NOT A: | 0 |
| Probability of event that occurs P(A) | 0 |
| Probability of event that does not occurs P(A') | 0 |
What is Probability?
If there are “ n “ elementary events associated with the random experiment and “ m “ of them are favourable to an event” A “ then the probability of happening or occurrence of event “ A “ is denoted by P ( A ) and is defined as the ratio $\frac{m}{n}$
Thus,
P ( A ) = $\frac{m}{n}$ = $\frac{Favourable\: number\: of\: elementary\: events}{Total\: number\: of\: elemnetary\: events}$
By the favourable number of events we mean that – An elementary event is said to be favourable to a compound event A, if it satisfies the definition of compound events A.
Let us consider an example. Consider a random experiment of throwing a pair of dice and the compound event “ A “ defined by getting 8 as the sum. We observe that event A occurs if we get any one of the following elementary events as the outcome – ( 2 , 6 ) , ( 6 , 2 ), ( 3 , 5 ) and ( 4 , 4 ). So there are 5 elementary events favourable to the event A.
How to find the probability of an event?
Let us see how we can find the probability of an event. We shall discuss it using an example.
Example
Suppose two unbiased coins are tossed simultaneously. What will be the probability of getting two heads?
Solution
If two unbiased coins are tossed simultaneously, we will get any one of the following as an outcome –
{ H H, H T, T H, T T }
Therefore, total number of possible outcomes = 4
Now, two heads can be obtained if the event { H H } occurs. This means that –
Favourable number of outcomes = 1
Hence, the require probability = $\frac{Favourable\: number\: of\: elementary\: events}{Total\: number\: of\: elemnetary\: events}$ = $\frac{1}{4}$
How to find the probability of a single event using the probability calculator?
There are different options available in the probability calculator such as finding the probability for one event, two events or multiple events.
Let us take the case where we need to find the probability of a single event. The following steps are to be followed for finding the probability using the calculator –
Step 1 – The first step is to choose the option for “ single event “ . Below is the highlighted option that we need to select for this purpose –
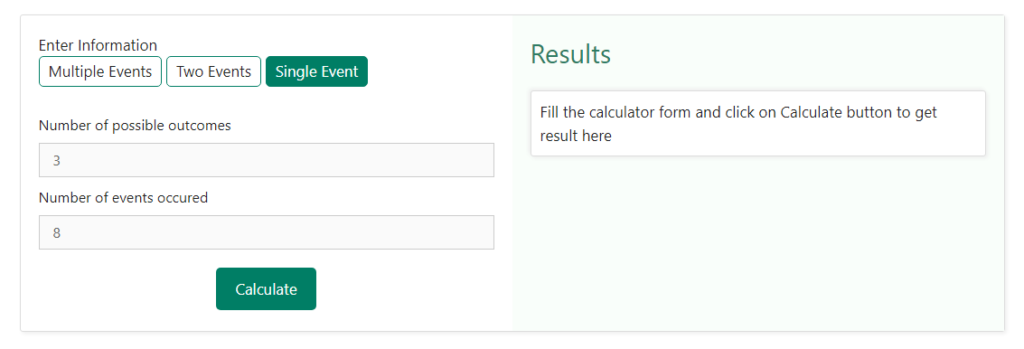
Step 2 – Once we have selected the choice of a single event, we need to enter the values of the “ favourable number of events “ and the “ total number of events “. For this purpose, let us take an example, where three unbiased coins are tossed together and we wish to find the probability of getting two heads. Now, we know that when three coins are tossed together, the total number of outcomes will be “ { H H H , H H T , H T H , T H H , H T T , T H T ,T T H ,T T T } = 8 outcomes. Now we wish to find the probability of getting two heads. Favourable outcomes in this case would be { H H T , T H H , H T H } = 3
Therefore, the probability in this case would be –
Favourable number of outcomes = 3
Total number of outcomes = 8
Probability = $\frac{Favourable\: number\: of\: elementary\: events}{Total\: number\: of\: elemnetary\: events}$ = $\frac{3}{8}$ = 0.375
Now, to do the same using the probability calculator, in this step, we just need to enter the values of the favourable number of outcomes and the total number of outcomes. Below is the snapshot that displays how these two values will be entered –
Step 2 – Now that we have entered the values of the favourable number of outcomes and the total number of outcomes we just need to click on the calculate button to get our result. As soon as we click on this button, we can see the result obtained on the right-hand side of the values that we had entered in the previous steps. Below is a snapshot of how the selection would look like when we will click on the “ calculate “ button –
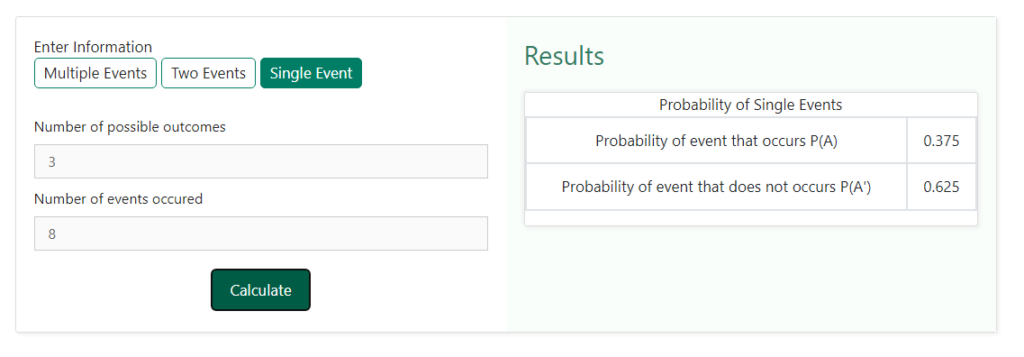
We can clearly see that the result obtained through the calculator as well the result obtained through the formula are the same. What’s more, the calculator also displays the formula as well as the steps involved in the calculation. The repeated use of this calculator allows you to not only check the results but also understand the formula and steps involved in finding the sides of a right angled triangle, thus allowing you to have a stronghold on the concept itself.
Moreover, the result displays both the probability of happening of the event and the probability of the event not happening.
Now, let us discuss the case of finding the probability of two events.
How to find the probability of multiple events?
The probability of multiple events occurs when we’re trying to calculate the probability of observing two or more events.
The probability of two events can be found by using the following formulas –
- P ( A ∪ B ) = P ( A ) + ( B ) – P ( A ∩ B )
- If A and B are mutually exclusive events, this means that P ( A ∪ B ) = 0, then we have, P ( A ∩ B ) = P ( A ) + ( B )
- If, A, B and C are mutually exclusive events then, P ( A ∩ B ) = P ( B ∩ C ) = P ( A ∩ C ) = P ( A ∩ B ∩ C ) = 0
How to find the probability of multiple events using the probability calculator?
The probability of multiple events can be found using the options of “ two events “ or multiple events in the probability calculator. Below is the snapshot that displays how these options can be chosen –
Suppose we choose the option of two events. We then need to enter the probabilities of the two events. Suppose we have P ( A ) = 0.8 and P ( B ) = 0.5. Below is the snapshot that displays how these values will be entered –
Now that we have entered probabilities of both the events we just need to click on the calculate button to get our result. As soon as we click on this button, we can see the result obtained on the right-hand side of the values that we had entered in the previous steps. Below is a snapshot of how the selection would look like when we will click on the “ calculate “ button –

We can see that the result gives us all the probable options for both the events which would definitely prove extremely handy when solving probability questions.