Triangle Calculator. Find the area, base b, height, side a, side c, side d, gamma and perimeter of a Triangle with our free to use calculator. Fantastic math tool. Click below to utilise it right now.
What is a triangle?
The word triangle is made from two words – “tri” which means three and “angle”. Hence, a triangle can be defined as a closed figure that has three vertices, three sides, and three angles.
How is the area of a triangle calculated?
A triangle is a polygon that is made of three edges and three vertices. The vertices join together to make three sides of a triangle. The area occupied between these three sides is called the area of a triangle.
What is the formula for finding the Area of a Triangle?
In general, the area of a triangle is defined by 1/2 x b x h
Area of a triangle = 1/2 x b x h
where b = base of the triangle (or any one side of the triangle), and
H = Height of the triangle from that base (or side)
Let us understand this more through an example. Suppose we have a triangle that has one side as 6 cm and an altitude (height) of 8 cm on that base.
The area of this triangle is given by
1/2 x b x h
Where b = 6 cm and h = 8 cm
Therefore, Area = 1/2 x 6 x 8 = 24 cm2
How the area of a triangle is calculated when the three sides are known?
When we know the three sides of a triangle and wish to find its area, we use Heron’s formula. There are two steps involved while using Heron’s formula –
First, we need to find the semi-perimeter of the triangle. The semi perimeter of a triangle having sides a, b and c is given by
Semi – Perimeter ( s ) = ( a b + c ) / 2
Now, the Heron’s formula is given by
Area of a Triangle = $\sqrt{s ( s-a )( s-b )( s-c )}$
Where a, b and c are the sides of a triangle and s is the semi-perimeter of the triangle.
Let us understand it through an example.
Suppose we have a triangle whose sides are 4 cm, 6 cm and 8 cm respectively. Let us use Heron’s formula to find the area of this triangle.
The semi – perimeter of this triangle will be given by
s = ( 4 + 6 + 8 ) / 2 = 18 / 2 = 9
Substituting the values of a, a, b and c in Heron’s formula, we will have,
Area of the Triangle = $\sqrt{(9 ( 9-4 )( 9-6 )( 9-8 ))}$
⇒ Area of the Triangle = $\sqrt{(9 x 5 x 3 x 1)}$
⇒ Area of the Triangle = √135
⇒ Area of the Triangle = 11.6189… = 11.62 ( approx. )
How to find the area of a triangle using the triangle calculator when the three sides are known?
Let us now see how to use the triangle calculator for finding the area of a triangle when its three sides are known.
The following steps are to be followed for finding the area of the triangle –
Step 1 – The first step is to choose the option of solving for “ area “ from the drop-down option given in the “ Enter Information “ section. Below is a snapshot of how the drop-down box would like upon choosing the area as selection –

Step 2 – Once we have chosen “ Solving for the area “ of our option, the next side is to choose what is given to us. In the given section, we need to choose “ side a, base, side c “ as the option as we are given with the three sides of the triangle. Below is a snapshot of how the drop-down box would like upon choosing sides as selection –
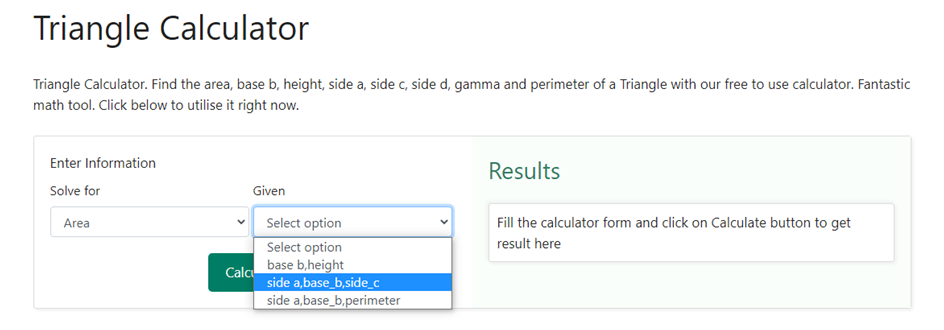
Step 3 – Now that we have chosen both what is required and what is given, we need to enter the value of the sides that is given to us. As soon as we choose side a, base, side c as the option in the previous step, three boxes crop up that asks us to enter the value of the sides of the triangle. Since we have been given the sides as 4 cm, 6 cm and 8 cm, we shall enter the same in the three boxes. Below is a snapshot of how the drop-down box would like upon having the requirement of entering the value of the sides –
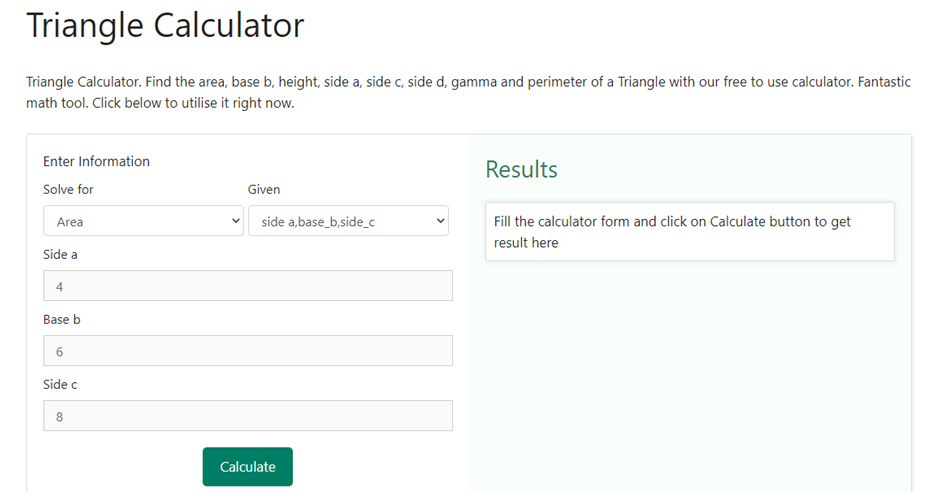
Step 4 – The last step is to click on the calculate button to obtain the value of the area. As soon as we will do that we shall have the results on the right hand side of the information that we entered in the above steps. Below is a snapshot of how the result would be displayed once we click on the calculate button.
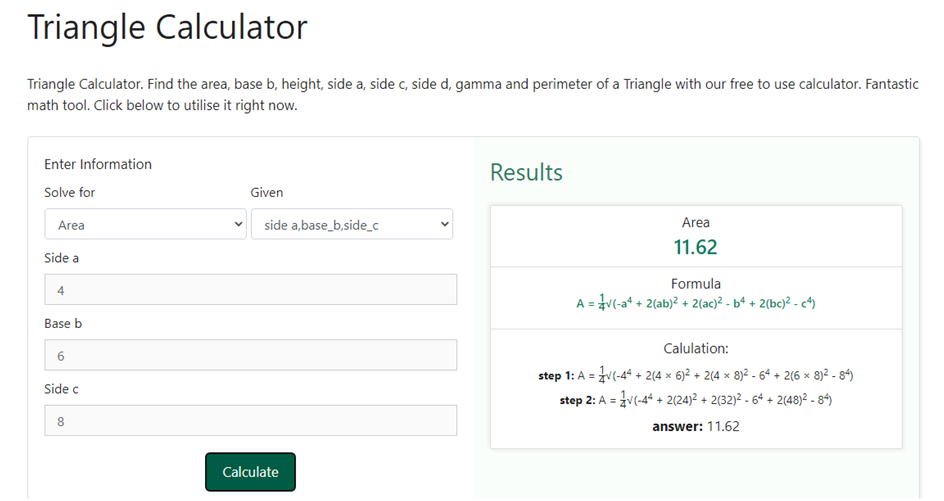
How to Find the Perimeter of a Triangle?
We know that the perimeter of any two-dimensional figure is defined as the distance around the figure. In the case of a triangle, the sum of lengths of all its three sides is its perimeter.
What is the formula for finding the Perimeter of a Triangle?
We know that in the case of a triangle, the perimeter will be the sum of all three sides. Therefore, if we have a triangle having three sides, namely, a, b and c, then the perimeter of the triangle is given by
Perimeter ( P ) = a + b + c
Let us understand it through an example.
Suppose we have a triangle having sides 4 cm, 6 cm, and 8 cm respectively. The perimeter of this triangle will be given by
Perimeter ( P ) = a + b + c = 4 + 6 + 8 = 18 cm
How the find the perimeter of a triangle using the triangle calculator when the three sides are known?
Step 1 – The first step is to choose the option of solving for “ perimeter “ from the drop-down option given in the “ Enter Information “ section. Below is a snapshot of how the drop-down box would like upon choosing the area as selection –
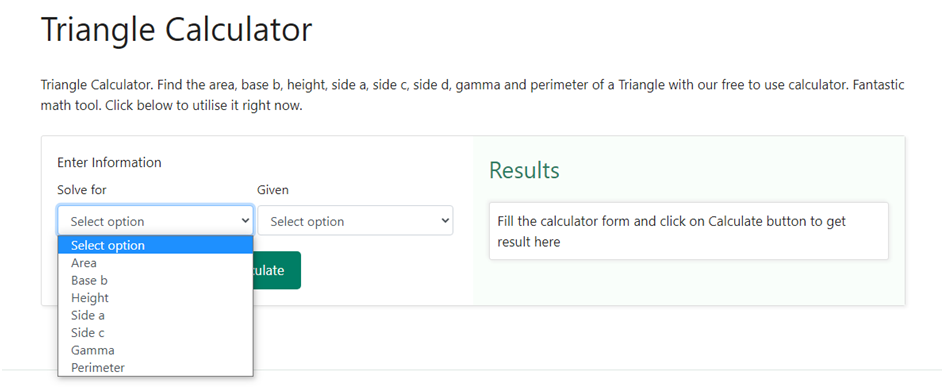
Step 2 – Once we have chosen “ Solving for the perimeter “ of our option, the next side is to choose what is given to us. In the given section, we need to choose “ side a, base, side c “ as the option as we are given with the three sides of the triangle. Below is a snapshot of how the drop-down box would like upon choosing perimeter as selection –
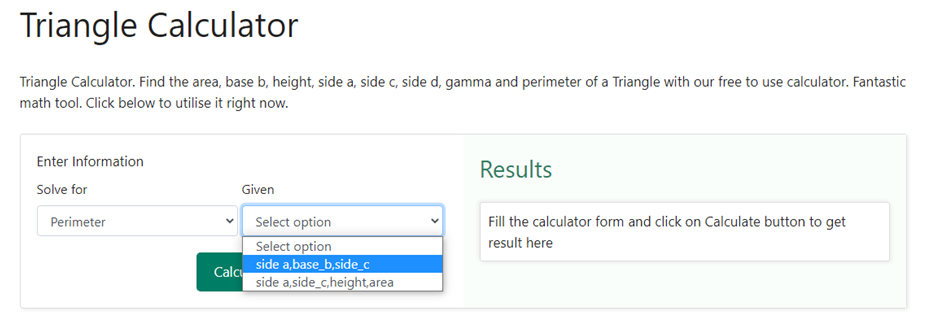
Step 3 – Now that we have chosen both what is required and what is given, we need to enter the value of the sides that is given to us. As soon as we choose side a, side b, side c as the option in the previous step, three boxes crop up that asks us to enter the value of the sides of the triangle. Suppose we have been given the sides as 4 cm, 6 cm and 8 cm, we shall enter the same in the three boxes. Below is a snapshot of how the drop-down box would like upon having the requirement of entering the value of the sides –
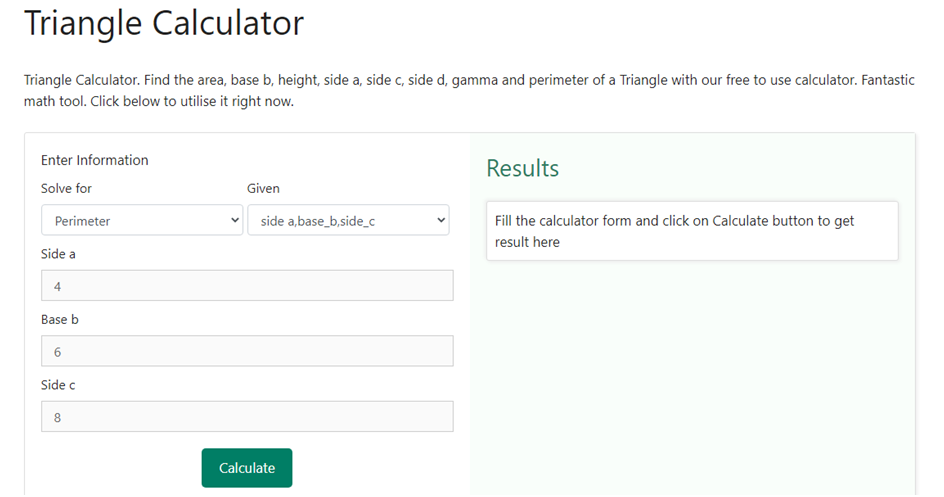
Step 4 – The last step is to click on the calculate button to obtain the value of the perimeter. As soon as we will do that we shall have the results on the right hand side of the information that we entered in the above steps. Below is a snapshot of how the result would be displayed once we click on the calculate button.
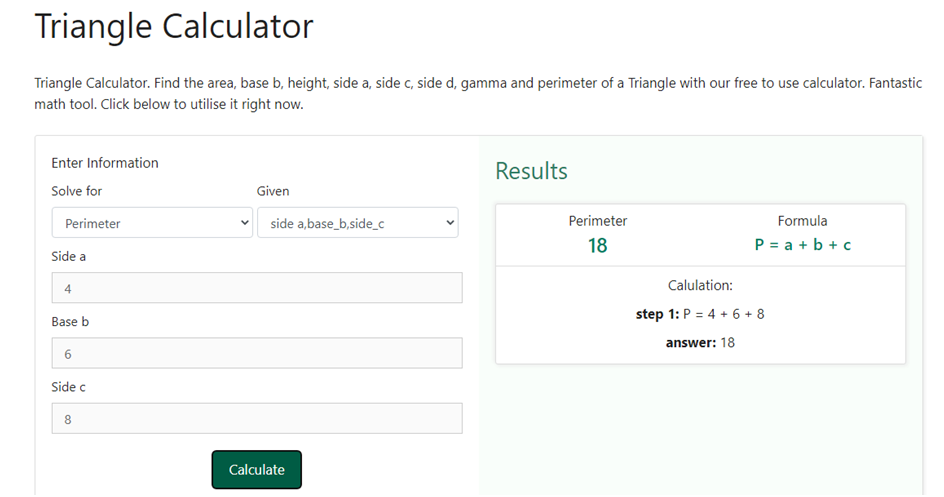
We can clearly see that only do we get the answer we also get to know the formula used as well as the steps involved in the calculation. This not only helps us to verify our answers but also helps us in having getting to learn more about the concepts related to the area of the circle and other dimensions related to it.