Rectangle Area Calculator. Find the length, width & diagonal of a rectangle with our free to use calculator. Fantastic math tool. Click below to utilise it right now.
How the area of a rectangle is calculated using an online calculator?
Below is a sneak peek of some of the options that are available in our rectangle area calculator. It can be clearly seen that one can choose options such as length and width, length and diagonal etc. you just need to enter the values and our calculator will do the rest for you.

The use of this calculator will not only ease your calculations but help you understand and learn how the area of a rectangle is calculated using different dimensions such as length, breadth, diagonals etc.
What is a rectangle?
We know that a rectangle is a type of quadrilateral that is similar to a square in the fact that it has equal opposite sides and four right angles. The properties of a rectangle are –
- A rectangle has two pairs of parallel sides
- A rectangle has four right angles
- A rectangle has opposite sides of equal lengths
- The diagonals of a rectangle bisect each other
Units of measurements of Area
The units used to measure area are based on the units of length, i.e. mm, cm, m, km etc. to measure a region we use a square as a unit. Hence, the unit of area is a unit square. This is written as unit2. Let us see who the different units are used to represent the area of a surface.
Unit Area
mm – mm2 (1 mm2 is equal to 1 square millimetres)
cm – cm2 (1 cm2 is equal to 1 square centimetres)
m – m2 (1 m2 is equal to 1 square metres)
km – km2 (1 km2 is equal to 1 square kilometres)
mi – mi2 (1 mi2 is equal to 1 square miles)
How to choose the correct unit when representing the area of a rectangular shape?
The unit for measuring the area depends on the size of the area being used. For example, the area, of the following are usually measured as under –
A Stamp – in m2
A notebook – in cm2
The floor of a room – in m2
A city – in km2 or mi2
How do we find the area of a rectangle using the area formula?
We know that a rectangle is a type of quadrilateral that is similar to a square in the fact that it has equal opposite sides and four right angles. But, unlike square where the length and the breadth are the same, in rectangle, we have different dimensions of length and breadth. We also know that
Area of a rectangle = length x breadth.
This means that there can be different combinations of length, breadth, area and perimeter using which some of which we are required to find the dimensions of the other. Our online rectangle calculator just does that.
Let us understand it using an example –
Example
Find the area, in square metres, of a rectangle whose
a) length = 4.5 m and breadth = 1.6 m.
b) length = 3 dm 6 cm, breadth = 2 dm 9 cm
Solution
a) We have,
Length = 4.5 m and Breadth = 1.6 m
Area of the rectangle = Length x Breadth
Hence, Area of the rectangle = (4.5 x 1.6) m2 = 7.20 m2
b) We have,
Length = 3 dm 6 cm = (3 x 10 + 6) cm = 36 cm = 0.36 m (∵ 1 dm = 10 cm)
Breadth = 2 dm 9 cm = (2 x 10 + 9) cm = 29 cm = 0.29 m
Area of the rectangle = Length x Breadth
Hence, Area of the rectangle = (0.36 x 0.29) m2 = 0.1044 m2
What are the units in which we can measure the area of a rectangle? Let us find out.
Calculating the Area of a rectangle using the formula
Here we have a rectangle, covered with small squares. Each small square stands for 1 square centimetre, that is, each small square is cm on each side.
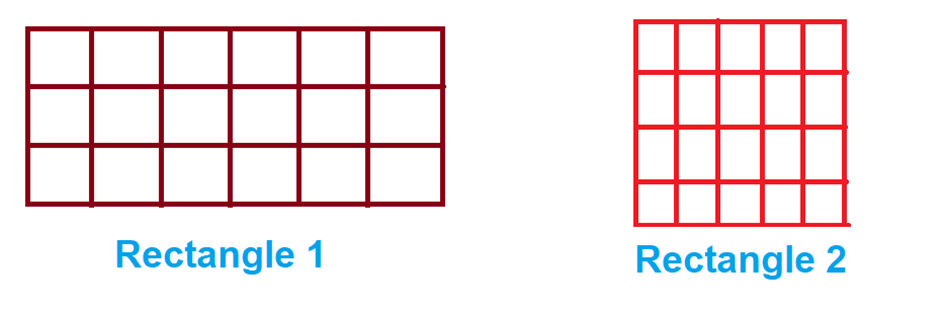
Count the number of squares that cover each rectangle. This will give you the area of a rectangle in square centimetres. Also, write the length and breadth of each rectangle. What do you observe?
Let’s find out.
Rectangle 1
Number of small squares = 18
Area = 18 cm2 or 18 sq. cm
Length = 6 cm
Breadth = 3 cm
Rectangle 2
Number of small squares = 20
Area = 20 cm2 or 20 sq. cm
Length = 5 cm
Breadth = 4 cm
From the above examples, you can see that there is a quicker way to find the area in each case without having to count the number of squares. Since 6 x 3 = 18 and 5 x 4 = 50, we can say that the area of each of the two rectangles can be found out by multiplying the measures of length and breadth of the rectangle.
Area of a rectangle having length ‘l’ and breadth ‘b’ is given by l x b
For example, let us consider a rectangle having a length of 8 cm and a breadth of 7 cm as shown in the figure below.

The area of this rectangle is given by 8 7 7 = 56 cm2.
Hence
Area of a rectangle = length x breadth
How to calculate the length and breadth of a rectangle using its area?
We now know how to calculate the area if we have the length and the breadth of a rectangle. But, if only the length or breadth and area are given, is it possible to know the breadth of the rectangle? Let us find out.
Since, Area of a rectangle = Length x Breadth,
Therefore,
Length = $\frac{Area}{Breadth}$, Breadth = $\frac{Area}{Length}$
Let us understand it more through an example.
Example
Let us understand it more through an example.
Example
Find the length of a rectangle, if its area = 90cm2 and breadth = 6 cm
Solution
We are given that area = 90cm2 and breadth = 10 cm
Now, Length = $\frac{Area}{Breadth}$
Hence, Length = $\frac{90}{6}$ cm = 15 cm
Therefore, the length of the rectangle having area = 90cm2 and breadth = 6 cm is 15 cm