Introduction
Around 2700 B.C., the Sumerians fictionalized their tool for calculation. The first Greek abacus was a table with a raised edge, crammed with sand. The columns were created by merely running your finger through the receptacle. The Romans created a lot of refined models of the grooved abacus. The wax replaced grooves cut straight into the wood, counters or beads were set in them. The Roman abacus was similar to the traditional Chinese abacus. The Roman abacus has been introduced to China for a while. Let us learn more about the abacus and how to use it to perform various mathematical operations.
Definition
Abacus means Abundant Beads Addition Calculation Utility System. Abacus is a simple tool used for performing rapid arithmetic calculations. Various types of hardwoods are used to make abacus. It is, in other words, a simple calculating device that consists of beads arranged in rods of wires embedded in a wooden frame. By sliding beads along the rods, various mathematical calculations can be performed. Let us now discuss the different parts of an abacus.
Parts of an Abacus
The following are the various parts that the abacus consists of –
Frame – The frame is the outer boundary of the abacus.
Rods and Beads – Each abacus consists of 17 rods and each rod has 15 beads.
Divisions – A horizontal bar divides the abacus into two divisions, the upper and the lower part. This horizontal bar is known as the beam.
Earth Beads – The beads that are in the lower part are called the lower beads or the earth beads.
Heaven Beads – The beads that are in the upper part is called the upper beads or the heaven beads.
Below is a pictorial representation of the parts of an abacus –

Advantages of using Abacus
Abacus is not just a tool for understanding various mathematical operations. It has a number of other advantages as well. The following are the advantages of using the abacus as a learning tool –
Mental arithmetic skills
Abacus is an excellent tool to help improve a child’s mental arithmetic skills.
Proficiency in Maths
Using an abacus in routine arithmetic operations in mathematics helps a child become proficient in mathematics.
Creativity
The use of the abacus allows a child to think creatively and understand the concepts in a better manner.
Listening Skills
Not just mathematical operations, but abacus also aids in improving the listening skills of a child.
Focus and Concentration
Since the abacus is more about mental calculations, it helps in improving the focus and concentration of a child.
Boost Confidence
When a child is able to perform mathematical calculations with ease it helps in boosting the confidence and aids in the overall personality development of the child as well.
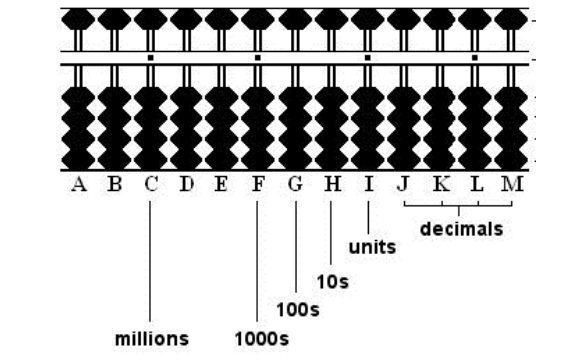
Understanding the Place Value system
Abacus uses the place system to represent the digits; therefore, it is important to understand the palace value system of numbers before we learn how to read the abacus. A place-value chart is a way to make sure digits are in the correct places. Let us understand how the place value chart is defined.
The place value chart of numbers is followed by most of the countries around the world. In this system, a number is split up into groups or periods. The following are the features of the International System of Numeration –
- We start from the extreme right digit of the number to form the groups.
- The groups are called ones, thousands, millions and billions.
- The ones, in turn, split up into hundreds, tens and units. The first three digits on the extreme right form a group of ones which in turn split into hundreds, tens and units.
- The second group of the next three digits on the left of the group of ones form the group of thousands which is further split into thousands, ten thousand and hundred thousand.
- The third group of the next three digits on the left of the group of thousands form the group of millions which is split into millions, ten million and hundred million.
- Three digits on the left of the group of millions form a group of billions which is split into billion, ten billions and hundred billion.
Types of Abacus
There are six main types of the abacus, namely –
- The Roman Abacus
- The Chinese Abacus
- The Japanese Soroban Abacus
- Russian Abacus
- Binary Abacus
- Cranmer Abacus
Let us learn about them one by one
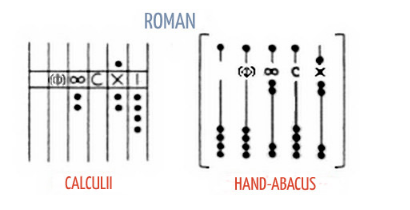
The Roman Abacus
Stones were used as counters by ancient Romans. This helped to maintain a smooth table of calculations up and down The Roman Abacus was developed for aiding the bankers and money changers, businessmen and engineers. Metal plates were used to make the Roman Abacus. Additionally Romans invented other types of Abacus such as the dust Abacus, the line Abacus, the grooved Abacus, etc.
The Chinese Abacus
The Abacus is called “suanpan” in China. In the Chinese abacus, the left and right strings of beads are separated using a divider. There are a total of seven beads in the Chinese abacus, out of which two beads on the rods on one side while 5 beads on the rods are on the other side of the divider. Hexadecimal computation forms the base of the calculations of the Chinse abacus. Recall that The hexadecimal number system uses the base 16. Thus it has 16 possible digit symbols. It uses the digits 0 to 9 along with letters, A, B, C, D, E, and F as the 16 digit symbols. Similar to the octal number system, the hexadecimal number system is also a positional value system where each digit has its own value or weight expressed as a power of 16. The places to the left of the hexadecimal point are positive powers of 16 and places to the right are negative powers of 16.
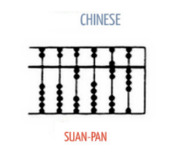
Decimal computations can also be performed using the Chinese abacus. Recall that The decimal number system is composed of 10 numerals or symbols. The word “ Deca “ means 10, which is why the system is known as the decimal number system. What are these 10 numerals that comprise the decimal number system? These numerals are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. Using these numerals, any number or quantity can be represented. The decimal number system uses the base 10. This means that 65410, 12510 are examples of numbers represented in the decimal number system. Therefore, every position in the decimal number system shows a particular power of the base ( 10 ). So, the Chinese abacus can be used for doing division, multiplication and for taking square roots and cube roots as well.
The Japanese Soroban Abacus
The Japanese Soroban abacus came into existence in the 14th century, having derived inspiration from the Chinese Suanpan. Wood is used to make the beads in the Japanese Soroban abacus and bamboo rods are used to slide up and down. This Japanese Soroban Abacus is still in use although it is fast losing its popularity due to the increase in the use of electronic calculators.
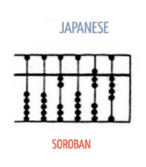
In the Japanese Soroban abacus, the beads are arranged according to place value from right to left.
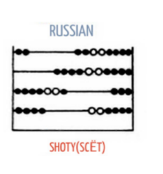
The Russian Abacus
The Russian abacus is quite similar to the Chinese abacus, with the main difference being the position of its rods. The rods in the Russian abacus are placed horizontally in the case of the Russian Abacus and beads are slid from the right to left. A typical Russian Abacus would measure 28 cm wide and 46 cm in height.
Binary Abacus
The use of the abacus in recent times is not just limited to performing arithmetic operations. It is also used to explain how Computers would manipulate numbers. A binary Abacus is used to perform one such function. It teaches us the conversion of decimals into binary. A series of the beads are placed in three separate rows, where each bead is associated with counters as ‘on’ and ‘off’ or ‘1’ and ‘0’. Recall that in the binary number system, there are only two possible digit values, 0 and 1. This is the reason, Binary number system is also known as the base – 2 number system. It is also a positional value system where each binary digit has its own value or weight expressed as a power of 2. In fact, the digits 0 and 1 are called bits and 8 bits together make a byte. The data in computers is stored in terms of bits and bytes. For example, 1011012 and 10112 are examples of the binary number system.
Cranmer Abacus
Tim Cranmer is credited to have made the Cranmer abacus. This is known to be the modification of the current Abacus to support the learners that have vision disabilities. The learners can manipulate the beads which would in effect help them in the in-depth understanding of the numbers. Various numbers involving arithmetic processes like addition, subtraction, division or multiplication can be calculated using Cranmer’s abacus. The Cranmer’s abacus can also be used to calculate square roots and cube roots which are considered advanced mathematical calculations.
Reading Numbers on the Abacus
The following points need to be kept in mind while reading numbers on the abacus –
- The column that is on the extreme right is for the one’s place.
- The next column is used for the ten’s place.
- The third column from the right end is for the hundred’s place and so on.
- This is similar to the place value system that we discussed above.
Use of Abacus
The following are the uses of using abacus –
- Abacus is used to perform simple arithmetic operations such as addition, subtraction, multiplication and division.
- Abacus can also be used to find the square root and the cube root of a number.
- Abacus instils confidence in the minds of the students as it removes the fear of mathematics.
Representation of Numbers on the Abacus
We can show 1000 on an abacus with four vertical rods. The rods represent place values of thousands, hundreds, tens and ones. We add beads on the rods to show different numbers. Each rod can hold up to 9 beads.
Let us understand it using an example –
- The first step is to arrange the abacus. The beads of the abacus will be in their original position which means no beads will touch the reckoning bar. And showing the number zero.
- Next, a place name is assigned to each vertical rod, similar to the place value system of numbers. The rightmost rod is named as Ones followed by tens, hundreds, and so on. We can assign a decimal place also. If we want to represent a decimal number such as 15.5 then the rightmost column will be the tenth place, earlier it was one’s place and followed by the place of the whole numbers such as ones and tens.
- Next, we start the counting from the bottom deck. As the bottom row has only four beads to make a number more than 4, we have to move back the bottom deck’s bead to its original position and bring down the heaven bead towards the reckoning bar.
Let us consider an example.
Let us learn to do simple counting from 0 to 9 on the abacus. To represent 1 on the abacus, we add 1 by moving 1 lower bead to the bar with our thumb. To add the numbers 2, 3, and 4 we simply move the corresponding number of lower beads to the bar with our thumb. To add 5 just move the upper heavenly bead to the bar with your index finger. To represent the number 6 on the abacus we grab both the upper 5 beads and 1 lower bead at the same time pinching both beads to the bar with our index finger and thumb. The number 7 would be the upper 5 beads with 2 lower beads. The number 8 is the upper 5 bead with 3 lower beads. And finally, represent the number 9 by pinching all the beads on the rod to the bar.
Addition and Subtraction using the abacus
Simple arithmetic operations such as addition and subtraction can be performed using the abacus.
The 10 Strategy
The following are the steps involved in this method –
- If we have to add 9 + 6, we will enter 6 and 9 in the first two columns.
- Then move from 6 to 9 so that 9 becomes 10 and 6 becomes 5.
- So now we can easily operate 10 + 5 = 15
The Two – 5 s strategy
If we have to add 9 + 8, we will enter 9 and 8 in the first two wires. The two 5s will make it 10, and we will remain with 7 beads. Now performing 10 + 7 = 17 is an easy exercise.
Now, we know that subtraction is the opposite of addition. Let us understand subtraction using an abacus through an example.
Example
Suppose we wish to subtract 662 from 945
- Enter 945 in the abacus and start subtracting column by column from the left.
- If we subtract 2 from 5, we will get 3 in the one’s place.
- Follow a similar method for ten’s places. Since we cannot subtract 6 from 4, we will have to borrow 1 from the hundred’s place, leaving 8 in the hundred’s place. Now we will get 14 in the ten’s place. Subtracting 6 from 14 we get 8 in the ten’s place.
- Finally, in the hundred’s place, we will subtract 6 from 9 and thus will be left with 3 beads.
- So our final answer will be 945 – 662 = 283.
Difference between Abacus and Vedic Mathematics
The following are the difference between the abacus and Vedic mathematics, though both are used as tools to learn various mathematical operations.
| Abacus | Vedic Mathematics |
| Abacus is considered as a brain development tool | Vedic mathematics is considered as a calculation improvement tool |
| Abacus aids in concentration building | Vedic mathematics helps to do calculations in a faster manner |
| Abacus tool is required for performing calculations | Pen and paper is required for performing calculations |
| Abacus is considered a part of Mental Maths | Vedic mathematics is considered a part of conditional maths |
Key Facts and Summary
- Abacus means Abundant Beads Addition Calculation Utility System.
- The frame is the outer boundary of the abacus.
- Each abacus consists of 17 rods and each rod has 15 beads.
- A horizontal bar divides the abacus into two divisions, the upper and the lower part. This horizontal bar is known as the beam.
- The beads that are in the lower part are called the lower beads or the earth beads.
- The beads that are in the upper part are called the upper beads or the heaven beads.
- A place-value chart is a way to make sure digits are in the correct places.
- We can show 1000 on an abacus with four vertical rods. The rods represent place values of thousands, hundreds, tens and ones. We add beads on the rods to show different numbers. Each rod can hold up to 9 beads.
Recommended Worksheets
Place Value (International Children’s Day Themed) Math Worksheets
Natural Numbers (Arbor Day Themed) Math Worksheets
Fact Families for Addition and Subtraction (Christmas Themed) Math Worksheets









